Giải SGK Toán 12 Cánh Diều Bài 3: Biểu thức tọa độ của các phép toán vectơ

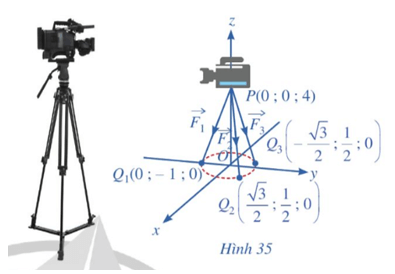
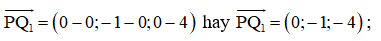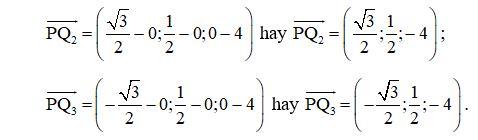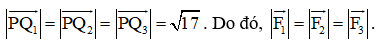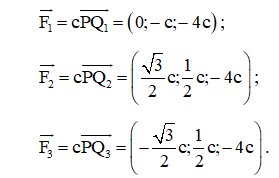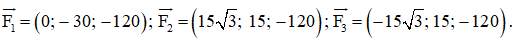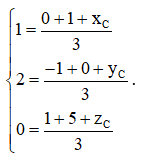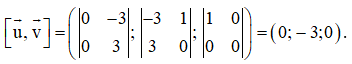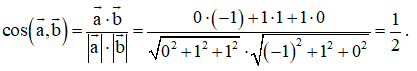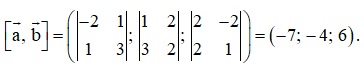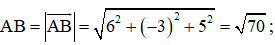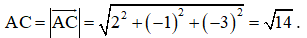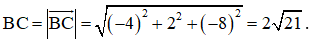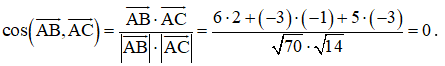Câu hỏi khởi động: Một chiếc máy quay phim ở đài truyền hình được đặt trên một giá đỡ ba chân với điểm đặt P(0; 0; 4) và các điểm tiếp xúc với mặt đất của ba chân lần lượt là Q1(0; – 1; 0), Q2 $\left(\frac{\sqrt{3}}{2};\frac{1}{2};0\right)$, Q3 $\left(-\frac{\sqrt{3}}{2};\frac{1}{2};0\right)$  (Hình 35). Biết rằng trọng lượng của máy quay là 360 N.

Làm thế nào để tìm được tọa độ của các lực $\overrightarrow{F_1},\overrightarrow{F_2},\overrightarrow{F_3}$  tác dụng lên giá đỡ?

Trả lời:

Theo giả thiết, ta có các điểm P(0; 0; 4), Q1(0; – 1; 0), Q2 $\left(\frac{\sqrt{3}}{2};\frac{1}{2};0\right)$, Q3 $\left(-\frac{\sqrt{3}}{2};\frac{1}{2};0\right)$.

Suy ra 

Suy ra 

Vì vậy, tồn tại hằng số c ≠ 0 sao cho:

Suy ra $\overrightarrow{F_1}+\overrightarrow{F_2}+\overrightarrow{F_3}=\left(0;0;-12c\right)$ .

Mặt khác, ta có: $\overrightarrow{F_1}+\overrightarrow{F_2}+\overrightarrow{F_3}=\overrightarrow{F}$ , trong đó $\overrightarrow{F}=\left(0;0;-360\right)$  là trọng lực tác dụng lên máy quay. Suy ra – 12c = – 360, tức là c = 30.

 Vậy 

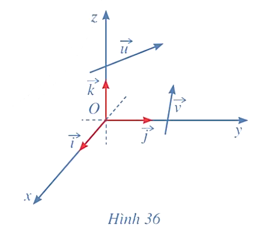
Hoạt động 1: Trong không gian với hệ tọa độ Oxyz (Hình 36), cho hai vectơ $\overrightarrow{u}=\left(x_1;y_1;z_1\right)$ và $\overrightarrow{v}=\left(x_2;y_2;z_2\right)$.

a) Biểu diễn các vectơ $\overrightarrow{u},\overrightarrow{v}$ theo ba vectơ $\overrightarrow{i},\overrightarrow{j},\overrightarrow{k}$.

b) Biểu diễn các vectơ $\overrightarrow{u}+\overrightarrow{v},\overrightarrow{u}-\overrightarrow{v},m\overrightarrow{u}$ (m ∈ ℝ) theo ba vectơ $\overrightarrow{i},\overrightarrow{j},\overrightarrow{k}$.

c) Tìm tọa độ các vectơ $\overrightarrow{u}+\overrightarrow{v},\overrightarrow{u}-\overrightarrow{v},m\overrightarrow{u}$ (m ∈ ℝ).

Trả lời:

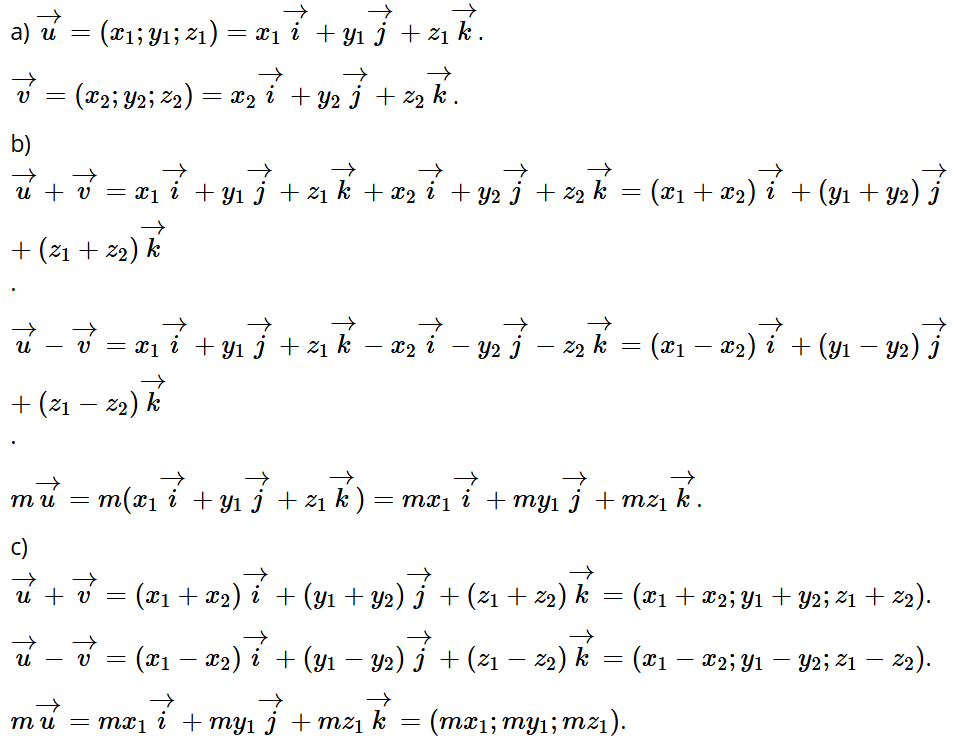
Luyện tập, vận dụng 1: 

a) Cho $\overrightarrow{u}=\left(-2;0;1\right),\overrightarrow{v}=\left(0;6;-2\right),\overrightarrow{w}=\left(-2;3;2\right)$. Tìm tọa độ của vectơ $\overrightarrow{u}+2\overrightarrow{v}-4\overrightarrow{w}$.

b) Cho ba điểm A(– 1; – 3; – 2), B(2; 3; 4), C(3; 5; 6). Chứng minh rằng ba điểm A, B, C thẳng hàng.

Trả lời:

a) Ta có $2\overrightarrow{v}=\left(0;12;-4\right),4\overrightarrow{w}=\left(-8;12;8\right)$ .

Do đó, $\overrightarrow{u}+2\overrightarrow{v}$ = (– 2 + 0; 0 + 12; 1 + (– 4)) = (– 2; 12; – 3).

Suy ra $\overrightarrow{u}+2\overrightarrow{v}-4\overrightarrow{w}$  = (– 2 – (– 8); 12 – 12; – 3 – 8).

Vậy $\overrightarrow{u}+2\overrightarrow{v}-4\overrightarrow{w}$  = (6; 0; – 11).

b) Ta có: $\overrightarrow{AB}$  = (2 – (– 1); 3 – (– 3); 4 – (– 2)) = (3; 6; 6),

               $\overrightarrow{AC}$  = (3 – (– 1); 5 – (– 3); 6 – (– 2)) = (4; 8; 8).

Ta có 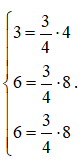 Từ đó suy ra $\overrightarrow{AB}=\frac{3}{4}\overrightarrow{AC}$.

Do đó, hai vectơ $\overrightarrow{AB}$ và $\overrightarrow{AC}$ cùng phương.

Suy ra hai đường thẳng AB và AC song song hoặc trùng nhau, mà AB ∩ AC = A.

Vậy hai đường thẳng AB và AC trùng nhau hay ba điểm A, B, C thẳng hàng.

II. Tọa độ trung điểm đoạn thẳng, tọa độ trọng tâm tâm giác

Hoạt động 2: 

a) Trong không gian với hệ tọa độ Oxyz, cho hai điểm A(xA; yA; zA) và B(xB; yB; zB). Gọi M(xM; yM; zM) là trung điểm của đoạn thẳng AB.

- Biểu diễn vectơ $\overrightarrow{OM}$ theo hai vectơ $\overrightarrow{OA}$ và $\overrightarrow{OB}$.

- Tính tọa độ của điểm M theo tọa độ của các điểm A(xA; yA; zA) và B(xB; yB; zB).

b) Trong không gian với hệ tọa độ Oxyz, cho tam giác ABC có trọng tâm G.

- Biểu diễn vectơ $\overrightarrow{OG}$ theo ba vectơ $\overrightarrow{OA}$, $\overrightarrow{OB}$ , $\overrightarrow{OC}$.

- Tính tọa độ của điểm G theo tọa độ của các điểm A(xA; yA; zA), B(xB; yB; zB), C(xC; yC; zC).

Trả lời:

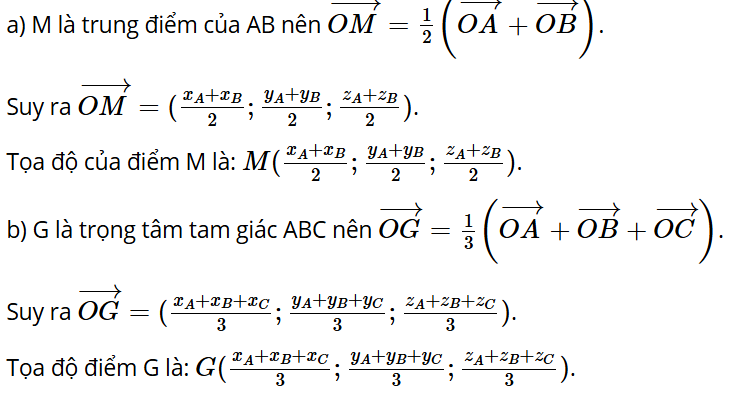
Luyện tập, vận dụng 2: Cho ba điểm A(0; – 1; 1), B(1; 0; 5), G(1; 2; 0).

a) Chứng minh rằng ba điểm A, B, G không thẳng hàng.

b) Tìm tọa độ điểm C sao cho G là trọng tâm của tam giác ABC.

Trả lời:

a) Ta có $\overrightarrow{AB}=\left(1;1;4\right),\overrightarrow{AG}=\left(1;3;-1\right)$.

Suy ra $\overrightarrow{AB}=\left(1;1;4\right)\ne k\overrightarrow{AG}=\left(k;3k;-k\right)$ với mọi k ∈ ℝ nên hai vectơ $\overrightarrow{AB}$  à $\overrightarrow{AG}$ không cùng phương.

Vậy ba điểm A, B, G không thẳng hàng.

b) Gọi tọa độ điểm C là (xC; yC; zC).

Vì G là trọng tâm của tam giác ABC nên ta có 

Suy ra xC = 3 – 1 = 2, yC = 6 + 1 = 7, zC = 0 – 6 = – 6.

Vậy C(2; 7; – 6).

III. Biểu thức tọa độ của tích vô hướng

Hoạt động 3: Trong không gian với hệ tọa độ Oxyz, cho các vectơ $\overrightarrow{u}=\left(x_1;y_1;z_1\right)$, $\overrightarrow{v}=\left(x_2;y_2;z_2\right)$.

Hãy biểu diễn các vectơ $\overrightarrow{u},\overrightarrow{v}$ theo ba vectơ đơn vị $\overrightarrow{i},\overrightarrow{j},\overrightarrow{k}$ và tính tích vô hướng $\overrightarrow{u}\cdot \overrightarrow{v}$.

Trả lời:

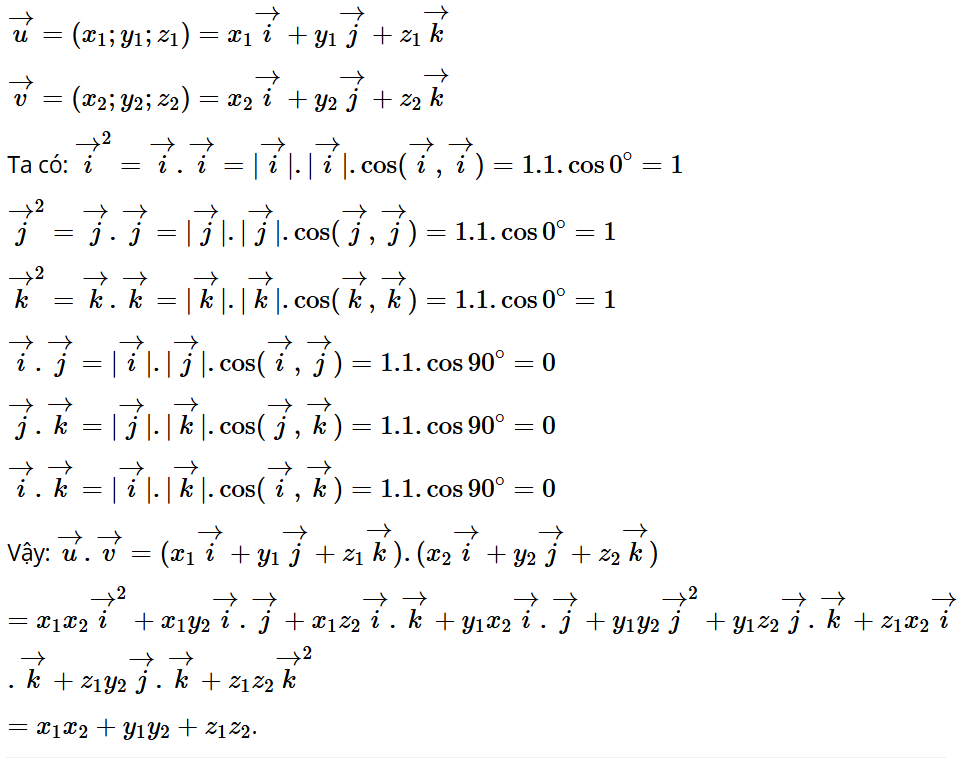
Luyện tập, vận dụng 3: Trong không gian với hệ tọa độ Oxyz, cho tam giác ABC có A(2; – 1; 1), B(1; – 1; 2) và C(3; 0; 2). Chứng minh rằng tam giác ABC vuông tại A.

Trả lời:

Ta có $\overrightarrow{AB}=\left(-1;0;1\right),\overrightarrow{AC}=\left(1;1;1\right)$.

Nhận thấy (– 1) ∙ 1 + 0 ∙ 1 + 1 ∙ 1 = – 1 + 1 = 0, do đó $\overrightarrow{AB}\cdot \overrightarrow{AC}=0$.

Suy ra hai vectơ $\overrightarrow{AB}$ và $\overrightarrow{AC}$ vuông góc với nhau hay hai đường thẳng AB và AC vuông góc với nhau.

Vậy tam giác ABC vuông tại A.

IV. Cách tìm tọa độ của một vectơ vuông góc với hai vectơ cho trước

Hoạt động 4: 

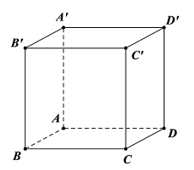
a) Cho hình lập phương ABCD.A'B'C'D' có A(0; 0; 0), B(1; 0; 0), D(0; 1; 0), C'(1; 1; 1). Hãy chỉ ra tọa độ của một vectơ vuông góc với cả hai vectơ $\overrightarrow{AB}$ và $\overrightarrow{AD}$.

b) Cho hai vectơ $\overrightarrow{u}=\left(x_1;y_1;z_1\right)$ và $\overrightarrow{v}=\left(x_2;y_2;z_2\right)$  không cùng phương.

Xét vectơ $\overrightarrow{w}=\left(y_1{z}_2-y_2{z}_1;z_1{x}_2-z_2{x}_1;x_1{y}_2-x_2{y}_1\right)$.

- Tính $\overrightarrow{w}\cdot \overrightarrow{u},\overrightarrow{w}\cdot \overrightarrow{v}$.

- Vectơ $\overrightarrow{w}$ có vuông góc với cả hai vectơ $\overrightarrow{u}$ và $\overrightarrow{v}$ hay không?

Trả lời:

a)

Luyện tập, vận dụng 4: Trong không gian với hệ tọa độ Oxyz, cho hai vectơ $\overrightarrow{u}=\left(1;0;-3\right)$ và $\overrightarrow{v}=\left(0;0;3\right)$. Hãy chỉ ra tọa độ của một vectơ $\overrightarrow{w}$ khác $\overrightarrow{0}$ vuông góc với cả hai vectơ $\overrightarrow{u}$ và $\overrightarrow{v}$.

Trả lời:

Ta có 

Chọn $\overrightarrow{w}$  = (0; – 3; 0).

Vậy vectơ $\overrightarrow{w}$  vuông góc với cả hai vectơ $\overrightarrow{u}$  và $\overrightarrow{v}$ .

Bài tập

Bài tập 1: Trong không gian với hệ tọa độ Oxyz, cho $\overrightarrow{a}=\left(2;3;-2\right)$ và $\overrightarrow{b}=\left(3;1;-1\right)$. Tọa độ của vectơ $\overrightarrow{a}-\overrightarrow{b}$ là:

A. (1; – 2; 1).

B. (5; 4; – 3).

C. (– 1; 2; – 1).

D. (– 1; 2; – 3).

Đáp án: C

Giải thích: Ta có $\overrightarrow{a}-\overrightarrow{b}$  = (2 – 3; 3 – 1; – 2 – (– 1)). Do đó $\overrightarrow{a}-\overrightarrow{b}$  = (– 1; 2; – 1).

Bài tập 2: Trong không gian với hệ tọa độ Oxyz, cho $\overrightarrow{a}=\left(0;1;1\right)$ và $\overrightarrow{b}=\left(-1;1;0\right)$ . Góc giữa hai vectơ $\overrightarrow{a}$ và $\overrightarrow{b}$ bằng:

A. 60°.

B. 120°.

C. 150°.

D. 30°.

Đáp án: A

Giải thích:

Ta có 

Suy ra $\left(\overrightarrow{a},\overrightarrow{b}\right)=60°$.

Bài tập 3: Trong không gian với hệ tọa độ Oxyz, cho $\overrightarrow{a}=\left(-1;2;3\right)$, $\overrightarrow{b}=\left(3;1;-2\right),\overrightarrow{c}=\left(4;2;-3\right)$.

a) Tìm tọa độ của vectơ $\overrightarrow{u}=2\overrightarrow{a}+\overrightarrow{b}-3\overrightarrow{c}$.

b) Tìm tọa độ của vectơ $\overrightarrow{v}$ sao cho $\overrightarrow{v}+2\overrightarrow{b}=\overrightarrow{a}+\overrightarrow{c}$ .

Trả lời:

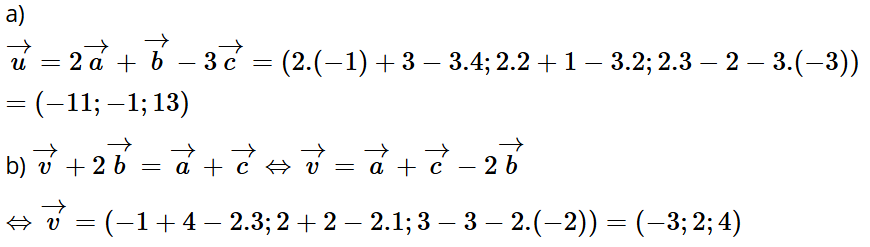
Bài tập 4: Trong không gian với hệ tọa độ Oxyz, cho $\overrightarrow{a}=\left(2;-2;1\right),\overrightarrow{b}=\left(2;1;3\right)$. Hãy chỉ ra tọa độ của một vectơ $\overrightarrow{c}$ khác $\overrightarrow{0}$ vuông góc với cả hai vectơ $\overrightarrow{a}$ và $\overrightarrow{b}$.

Trả lời:

Ta có 

Chọn $\overrightarrow{c}=\left(-7;-4;6\right)$ , ta có vectơ vectơ $\overrightarrow{c}$  vuông góc với cả hai vectơ $\overrightarrow{a}$  và $\overrightarrow{b}$ .

Bài tập 5: Trong không gian với hệ tọa độ Oxyz, cho $\overrightarrow{a}=\left(3;2;-1\right),\overrightarrow{b}=\left(-2;1;2\right)$. Tính côsin của góc $\left(\overrightarrow{a},\overrightarrow{b}\right)$.

Trả lời:

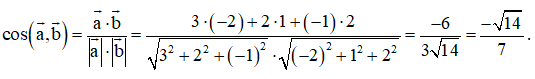
Bài tập 6: Trong không gian với hệ tọa độ Oxyz, cho A(– 2; 3; 0), B(4; 0; 5), C(0; 2; – 3).

a) Chứng minh rằng ba điểm A, B, C không thẳng hàng.

b) Tính chu vi tam giác ABC.

c) Tìm tọa độ trọng tâm G của tam giác ABC.

d) Tính $\cos \widehat{BAC}$.

Trả lời:

a) Ta có $\overrightarrow{AB}=\left(6;-3;5\right)$, $\overrightarrow{AC}=\left(2;-1;-3\right)$.

Suy ra $\overrightarrow{AB}=\left(6;-3;5\right)\ne k\overrightarrow{AC}=\left(2k;-k;-3k\right)$ với mọi k ∈ ℝ, do đó hai vectơ $\overrightarrow{AB}$ và $\overrightarrow{AC}$ không cùng phương.

Vậy ba điểm A, B, C không thẳng hàng.

b) Ta có 

Ta có $\overrightarrow{BC}=\left(-4;2;-8\right)$.

Suy ra 

Chu vi tam giác ABC là C = AB + AC + BC = $\sqrt{70}+\sqrt{14}+2\sqrt{21}$.

c) Gọi tọa độ trọng tâm G của tam giác ABC là (xG; yG; zG).

Ta có $x_G=\frac{-2+4+0}{3}=\frac{2}{3}$; $y_G=\frac{3+0+2}{3}=\frac{5}{3};z_G=\frac{0+5+\left(-3\right)}{3}=\frac{2}{3}$ .

Vậy $G\left(\frac{2}{3};\frac{5}{3};\frac{2}{3}\right)$ .

d) Ta có 

Do đó hai vectơ $\overrightarrow{AB}$ và $\overrightarrow{AC}$ vuông góc với nhau hay hai đường thẳng AB và AC vuông góc với nhau nên $\widehat{BAC}=90°$. Vậy $\cos \widehat{BAC}$ = 0.

Bài tập 7: Cho hình hộp ABCD.A'B'C'D', biết A(1; 0; 1), B(2; 1; 2), D(1; – 1; 1), C'(4; 5; – 5). Hãy chỉ ra tọa độ của một vectơ khác $\overrightarrow{0}$  vuông góc với cả hai vectơ trong mỗi trường hợp sau:

a) ${AC}^{}$ và $\overrightarrow{B^{\prime }{D}^{\prime }}$;

b) $\overrightarrow{A{C}^{\prime }}$ và $\overrightarrow{BD}$.

Trả lời:

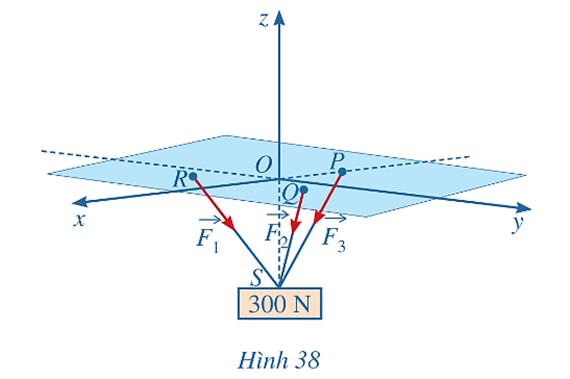
Bài tập 8: Một vật có trọng lượng 300 N được treo bằng ba sợi dây cáp không dãn có chiều dài bằng nhau, mỗi dây cáp có một đầu được gắn tại một trong các điểm P(– 2; 0; 0), Q(1; $\sqrt{3}$; 0), R(1; $-\sqrt{3}$; 0) còn đầu kia gắn với vật tại điểm S(0; 0; $-2\sqrt{3}$) như Hình 38. Gọi $\overrightarrow{F_1},\overrightarrow{F_2},\overrightarrow{F_3}$ lần lượt là lực căng trên các sợi dây cáp RS, QS và PS. Tìm tọa độ của các lực $\overrightarrow{F_1},\overrightarrow{F_2},\overrightarrow{F_3}$.

Trả lời:

Theo giả thiết, ta có các điểm S(0; 0; $-2\sqrt{3}$), P(– 2; 0; 0), Q(1; $\sqrt{3}$; 0), R(1; $-\sqrt{3}$; 0).

Khi đó: $\overrightarrow{SP}=\left(-2;0;2\sqrt{3}\right)$, $\overrightarrow{SQ}=\left(1;\sqrt{3};2\sqrt{3}\right)$, $\overrightarrow{SR}=\left(1;-\sqrt{3};2\sqrt{3}\right)$.

Suy ra $\left|\overrightarrow{SP}\right|=\left|\overrightarrow{SQ}\right|=\left|\overrightarrow{SR}\right|=4$. Lại có $\overrightarrow{PQ}=\left(3;\sqrt{3};0\right)$, $\overrightarrow{QR}=\left(0;-2\sqrt{3};0\right)$, $\overrightarrow{RP}=\left(-3;\sqrt{3};0\right)$, vì $\left|\overrightarrow{PQ}\right|=\left|\overrightarrow{QR}\right|=\left|\overrightarrow{RP}\right|=2\sqrt{3}$ nên tam giác PQR đều.

Do đó, $\left|\overrightarrow{F_1}\right|=\left|\overrightarrow{F_2}\right|=\left|\overrightarrow{F_3}\right|$. Vì vậy, tồn tại hằng số c ≠ 0 sao cho:

$\overrightarrow{F_1}=c\overrightarrow{SR}=\left(c;-\sqrt{3}c;2\sqrt{3}c\right)$,

$\overrightarrow{F_2}=c\overrightarrow{SQ}=\left(c;\sqrt{3}c;2\sqrt{3}c\right)$,

$\overrightarrow{F_3}=c\overrightarrow{SP}=\left(-2c;0;2\sqrt{3}c\right)$,

Suy ra $\overrightarrow{F_1}+\overrightarrow{F_2}+\overrightarrow{F_3}=\left(0;0;6\sqrt{3}c\right)$.

Mặt khác, ta có: $\overrightarrow{F_1}+\overrightarrow{F_2}+\overrightarrow{F_3}=\overrightarrow{F}$, trong đó $\overrightarrow{F}=\left(0;0;-300\right)$ là trọng lực của vật.

Suy ra $6\sqrt{3}c=-300$, tức là $c=\frac{-50\sqrt{3}}{3}$.

Vậy $\overrightarrow{F_1}=\left(\frac{-50\sqrt{3}}{3};50;-100\right)$, $\overrightarrow{F_2}=\left(\frac{-50\sqrt{3}}{3};-50;-100\right)$, $\overrightarrow{F_3}=\left(\frac{100\sqrt{3}}{3};0;-100\right)$.