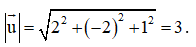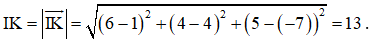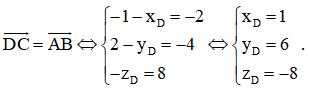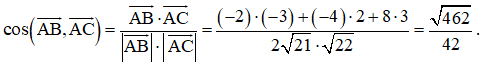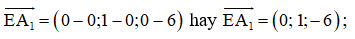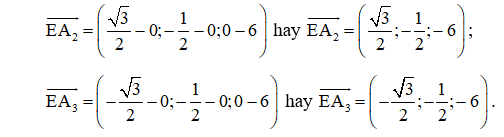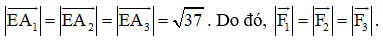Giải SGK Toán 12 Cánh Diều Bài tập cuối chương II

Bài tập 1: Cho điểm M thỏa mãn $\overrightarrow{OM}=3\overrightarrow{i}+4\overrightarrow{j}+2\overrightarrow{k}$. Tọa độ của điểm M là:

A. (2; 3; 4).

B. (3; 4; 2).

C. (4; 2; 3).

D. (3; 2; 4).

Đáp án: B

Giải thích: Ta có $\overrightarrow{OM}=3\overrightarrow{i}+4\overrightarrow{j}+2\overrightarrow{k}$, do đó M(3; 4; 2).

Bài tập 2: Cho hai điểm M(1; – 2; 3) và N(3; 4; – 5). Tọa độ của vectơ $\overrightarrow{NM}$ là:

A. (– 2; 6; 8).

B. (2; 6; – 8).

C. (– 2; 6; – 8).

D. (– 2; – 6; 8).

Đáp án: D

Giải thích: Ta có ${NM}^{}=\left(1-3;-2-4;3-\left(-5\right)\right)=\left(-2;-6;8\right)$.

Bài tập 3: Cho hai vectơ $\overrightarrow{u}=\left(3;-4;5\right),\overrightarrow{v}=\left(5;7;-1\right)$. Tọa độ của vectơ $\overrightarrow{u}+\overrightarrow{v}$ là:

A. (8; 3; 4).

B. (– 2; – 11; 6).

C. (2; 11; – 6).

D. (– 8; – 3; – 4).

Đáp án: A

Giải thích:

Ta có $\overrightarrow{u}+\overrightarrow{v}$  = (3 + 5; – 4 + 7; 5 + (– 1)).

Do đó, $\overrightarrow{u}+\overrightarrow{v}$  = (8; 3; 4).

Bài tập 4: Cho hai vectơ $\overrightarrow{u}=\left(1;–2;3\right),\overrightarrow{v}=\left(5;4;-1\right)$. Tọa độ của vectơ $\overrightarrow{u}-\overrightarrow{v}$ là:

A. (4; 6; 4).

B. (– 4; – 6; 4).

C. (4; 6; – 4).

D. (– 4; – 6; – 4).

Đáp án: B

Giải thích:

Ta có $\overrightarrow{u}-\overrightarrow{v}$  = (1 – 5; – 2 – 4; 3 – (– 1)).

Do đó, $\overrightarrow{u}-\overrightarrow{v}$  = (– 4; – 6; 4).

Bài tập 5: Cho vectơ $\overrightarrow{u}=\left(1;-1;3\right)$. Tọa độ của vectơ $-3\overrightarrow{u}$ là:

A. (3; – 3; 9).

B. (3; – 3; – 9).

C. (– 3; 3; – 9).

D. (3; 3; 9).

Đáp án: C

Giải thích: Ta có $-3\overrightarrow{u}$  = (– 3 ∙ 1 ; – 3 ∙ (– 1); – 3 ∙ 3) = (– 3; 3; – 9).

Bài tập 6: Độ dài của vectơ $\overrightarrow{u}=\left(2;-2;1\right)$ là:

A. 9.

B. 3.

C. 2.

D. 4.

Đáp án: B

Giải thích: Ta có 

Bài tập 7: Tích vô hướng của hai vectơ $\overrightarrow{u}=\left(1;-2;3\right)$ và $\overrightarrow{v}=\left(3;4;-5\right)$ là:

A. $\sqrt{14}\cdot \sqrt{50}$.

B. $-\sqrt{14}\cdot \sqrt{50}$.

C. 20.

D. – 20.

Đáp án: D

Giải thích: Ta có $\overrightarrow{u}\cdot \overrightarrow{v}=1\cdot 3+\left(-2\right)\cdot 4+3\cdot \left(-5\right)=-20$.

Bài tập 8: Khoảng cách giữa hai điểm I(1; 4; – 7) và K(6; 4; 5) là:

A. 169.

B. 13.

C. 26.

D. 6,5.

Đáp án: B

Giải thích: Ta có

Bài tập 9: Cho hai điểm M(1; – 2; 3) và N(3; 4; – 5). Trung điểm của đoạn thẳng MN có tọa độ là:

A. (– 2; 1; 1).

B. (2; 1; 1).

C. (– 2; 1; – 1).

D. (2; 1; – 1).

Đáp án: D

Giải thích:

Gọi tọa độ trung điểm của đoạn thẳng MN là (x; y; z).

Ta có $x=\frac{1+3}{2}=2;y=\frac{-2+4}{2}=1;z=\frac{3+\left(-5\right)}{2}=-1$.

Vậy tọa độ trung điểm của đoạn thẳng MN là (2; 1; – 1).

Bài tập 10: Cho tam giác MNP có M(0; 2; 1), N(–1; –2; 3) và P(1; 3; 2). Trọng tâm của tam giác MNP có tọa độ là:

A. (0; 1; 2).

B. (0; 3; 6).

C. (0; – 3; – 6).

D. (0; – 1; – 2).

Đáp án: A

Giải thích:

Gọi tọa độ trọng tâm của tam giác MNP là (x; y; z).

Ta có $x=\frac{0+\left(-1\right)+1}{3}=0;y=\frac{2+\left(-2\right)+3}{3}=1;z=\frac{1+3+2}{3}=2$.

Vậy tọa độ trọng tâm của tam giác MNP là (0; 1; 2).

Bài tập 11: Cho hai vectơ $\overrightarrow{u}=\left(1;-2;3\right)$ và $\overrightarrow{v}=\left(3;4;-5\right)$. Hãy chỉ ra tọa độ của một vectơ $\overrightarrow{w}$ khác $\overrightarrow{0}$ vuông góc với cả hai vectơ $\overrightarrow{u}$ và $\overrightarrow{v}$.

Trả lời:

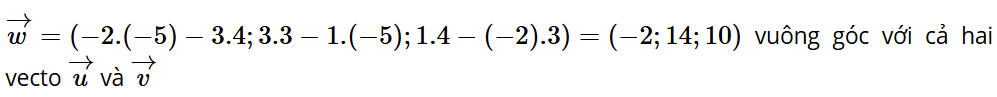
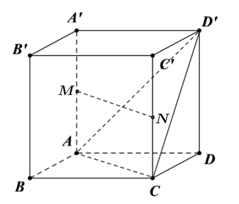
Bài tập 12: Cho hình lập phương ABCD.A'B'C'D' có cạnh bằng a. Gọi M, N lần lượt là trung điểm của các cạnh AA' và CC'. Tính góc giữa hai vectơ $\overrightarrow{MN}$ và $\overrightarrow{A{D}^{\prime }}$.

Trả lời:

Vì M, N lần lượt là trung điểm của các cạnh AA' và CC' nên MN // AC, MN = AC.

Suy ra $\overrightarrow{MN}=\overrightarrow{AC}$. Do đó, $\left(\overrightarrow{MN},\overrightarrow{A{D}^{\prime }}\right)=\left(\overrightarrow{AC},\overrightarrow{A{D}^{\prime }}\right)={\mathrm{CAD\prime ^\backslash widehat\{CAD\text{'}\}CAD\prime }}^{}$.

Ta tính được $A{D}^{\prime }=AC=C{D}^{\prime }=a\sqrt{2}$ nên tam giác ACD' là tam giác đều.

Suy ra ${\mathrm{CAD\prime ^\backslash widehat\{CAD\text{'}\}CAD\prime }}^{}=60°$.

Vậy $\left(\overrightarrow{MN},\overrightarrow{A{D}^{\prime }}\right)=60°$.

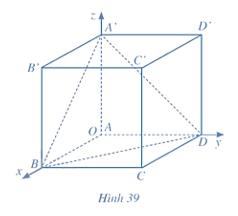
Bài tập 13: Xét hệ toạ độ Oxyz gắn với hình lập phương ABCD.A'B'C'D' như Hình 39, đơn vị của mỗi trục bằng độ dài cạnh hình lập phương. Biết A(0; 0; 0), B(1; 0; 0), D(0; 1; 0), A'(0; 0; 1).

a) Xác định toạ độ các đỉnh còn lại của hình lập phương ABCD.A'B'C'D'.

b) Xác định toạ độ trọng tâm G của tam giác A'BD.

c) Xác định toạ độ các vectơ $\overrightarrow{OG}$ và $\overrightarrow{O{C}^{\prime }}$. Chứng minh rằng ba điểm O, G, C' thẳng hàng và OG = $\frac{1}{3}$OC'.

Trả lời:

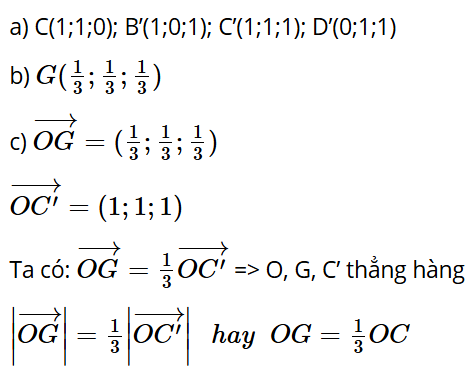
Bài tập 14: Trong không gian với hệ toạ độ Oxyz, cho A(2; 0; – 3), B(0; – 4; 5) và C(– 1; 2; 0).

a) Chứng minh rằng ba điểm A, B, C không thẳng hàng.

b) Tìm toạ độ của điểm D sao cho tứ giác ABCD là hình bình hành.

c) Tìm toạ độ trọng tâm G của tam giác ABC.

d) Tính chu vi của tam giác ABC.

e) Tính $\cos$$\widehat{BAC}$.

Trả lời:

a) Ta có $\overrightarrow{AB}=\left(-2;-4;8\right)$, $\overrightarrow{AC}=\left(-3;2;3\right)$.

Suy ra $\overrightarrow{AB}=\left(-2;-4;8\right)\ne k\overrightarrow{AC}=\left(-3k;2k;3k\right)$ với mọi k ∈ ℝ nên hai vectơ $\overrightarrow{AB}$ và $\overrightarrow{AC}$ không cùng phương.

Vậy ba điểm A, B, C không thẳng hàng.

b) Gọi tọa độ điểm D là (xD; yD; zD). Ta có $\overrightarrow{DC}$ = (– 1 – xD; 2 – yD; – zD).

Tứ giác ABCD là hình bình hành khi

Vậy D(1; 6; – 8).

c) Gọi tọa độ trọng tâm G của tam giác ABC là (xG; yG; zG).

Ta có

$x_G=\frac{2+0+\left(-1\right)}{3}=\frac{1}{3};y_G=\frac{0+\left(-4\right)+2}{3}=\frac{-2}{3};z_G=\frac{-3+5+0}{3}=\frac{2}{3}$

Vậy $G\left(\frac{1}{3};\frac{-2}{3};\frac{2}{3}\right)$ .

d) Ta có AB = $\left|\overrightarrow{AB}\right|=\sqrt{{\left(-2\right)}^2+{\left(-4\right)}^2+8^2}=2\sqrt{21}$;

              AC = $\left|\overrightarrow{AC}\right|=\sqrt{{\left(-3\right)}^2+2^2+3^2}=\sqrt{22}$;

              BC = $\left|\overrightarrow{BC}\right|=\sqrt{{\left(-1-0\right)}^2+{\left(2-\left(-4\right)\right)}^2+{\left(0-5\right)}^2}=\sqrt{62}$.

Chu vi tam giác ABC là C = AB + AC + BC = $2\sqrt{21}+\sqrt{22}+\sqrt{62}$.

e) Ta có

Lại có $\left(\overrightarrow{AB},\overrightarrow{AC}\right)={\mathrm{BAC^\backslash widehat\{BAC\}BAC}}^{}$. Do đó, $\cos {\mathrm{BAC^\backslash widehat\{BAC\}BAC}}^{}=\frac{\sqrt{462}}{42}$.

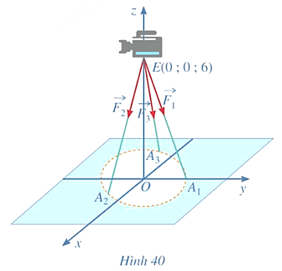
Bài tập 15: Một chiếc máy được đặt trên một giá đỡ ba chân với điểm đặt E(0 ; 0 ; 6) và các điểm tiếp xúc với mặt đất của ba chân lần lượt là A­­1(0; 1; 0), $A_2\left(\frac{\sqrt{3}}{2};-\frac{1}{2};0\right)$, $A_3\left(-\frac{\sqrt{3}}{2};-\frac{1}{2};0\right)$ (Hình 40). Biết rằng trọng lượng của chiếc máy là 300 N. Tìm tọa độ của các lực tác dụng lên giá đỡ $\overrightarrow{F_1},\overrightarrow{F_2},\overrightarrow{F_3}$.

Trả lời:

Theo giả thiết, ta có các điểm E(0; 0; 6), A­­1(0; 1; 0), $A_2\left(\frac{\sqrt{3}}{2};-\frac{1}{2};0\right)$, $A_3\left(-\frac{\sqrt{3}}{2};-\frac{1}{2};0\right)$ .

Suy ra 

Suy ra

Vì vậy, tồn tại hằng số c ≠ 0 sao cho:

$\overrightarrow{F_1}=c\overrightarrow{E{A}_1}=\left(0;c;-6c\right)$;

$\overrightarrow{F_2}=c\overrightarrow{E{A}_2}=\left(\frac{\sqrt{3}}{2}c;-\frac{1}{2}c;-6c\right)$;

$\overrightarrow{F_3}=c\overrightarrow{E{A}_3}=\left(-\frac{\sqrt{3}}{2}c;-\frac{1}{2}c;-6c\right)$.

Suy ra $\overrightarrow{F_1}+\overrightarrow{F_2}+\overrightarrow{F_3}=\left(0;0;-18c\right)$.

Mặt khác, ta có: $\overrightarrow{F_1}+\overrightarrow{F_2}+\overrightarrow{F_3}=\overrightarrow{F}$, trong đó $\overrightarrow{F}=\left(0;0;-300\right)$ là trọng lực tác dụng lên máy quay. Suy ra – 18c = – 300, tức là c = $\frac{50}{3}$.

 Vậy $\overrightarrow{F_1}=\left(0;\frac{50}{3};-100\right)$;

$\overrightarrow{F_2}=\left(\frac{25\sqrt{3}}{3};\frac{-25}{3};-100\right);$

$\overrightarrow{F_3}=\left(\frac{-25\sqrt{3}}{3};\frac{-25}{3};-100\right)$.