Câu hỏi khởi động: Thầy giáo chuẩn bị 30 miếng dứa và 48 miếng dưa hấu để liên hoan lớp. Thầy giáo muốn chia số trái cây trên vào một số đĩa sao cho mỗi đĩa có số miếng mỗi loại quả như nhau. Thầy giáo có thể chia như thế vào bao nhiêu đĩa? Số đĩa nhiều nhất mà thầy giáo có thể dùng là bao nhiêu?
Lời giải:
Trước khi học bài này, ta giải quyết bài toán như sau:
+) Ta tìm các ước của 30 và 48:
Các ước của 30 là: 1, 2, 3, 5, 6, 10, 15, 30.
Các ước của 48 là: 1, 2, 3, 4, 6, 8, 12, 16, 24, 48.
+) Các ước chung của của 30 và 48 là 1, 2, 3, 6
Vậy thầy giáo có thể chia số hoa quả thành 1 đĩa, 2 đĩa, 3 đĩa hoặc 6 đĩa. Số đĩa nhiều nhất mà thầy giáo có thể chia là 6 đĩa.
I. Ước chung và ước chung lớn nhất
Hoạt động 1:
a) Nêu các ước của 30 và của 48 theo thứ tự tăng dần:
b) Tìm các số vừa ở trong hàng thứ nhất vừa ở trong hàng thứ hai.
c) Xác định số lớn nhất trong các ước chung của 30 và 48.
Lời giải:
a) Các ước của 30 và của 48 theo thứ tự tăng dần:
b) Các số vừa ở hàng thứ nhất vừa ở hàng thứ 2 là: 1;2;3;6.
c) Số lớn nhất là 6.
Luyện tập, vận dụng 1:
a) Số 8 có phải là ước chung của 24 và 56 không? Vì sao?
b) Số 8 có phải là ước chung của 14 và 48 không? Vì sao?
Lời giải:
a) Số 8 là ước chung của 24 và 56 vì 8 vừa là ước của 24 vừa là ước của 56.
b) Số 8 không phải là ước chung của 14 và 48 vì 8 là ước của 48 nhưng không phải là ước của 14
Luyện tập, vận dụng 2: Số 7 có phải là ước chung của 14, 49, 63 không? Vì sao?
Lời giải:
Ta có: 14 : 7 = 2; 49 : 7 = 7; 63 : 7 = 9
Nên 7 là ước của cả ba số 14; 49 và 63.
Vậy 7 là ước chung của ba số 14; 49 và 63.
Hoạt động 2: Quan sát bảng sau:
a) Viết tập hợp ƯC(24, 36).
b) Tìm ƯCLN (24, 36).
c) Thực hiện phép chia ƯCLN (24, 36) cho các ước chung của hai số đó.
Lời giải:
a) Các ước chung của 24 và 36 là 1, 2, 3, 4, 6, 12.
Vậy ƯC(24, 36) = {1, 2, 3, 4, 6, 12}.
b) ƯCLN(24, 36) = 12.
c) ƯCLN(24, 36) = 12.
Chia ƯCLN cho các ước chung:
12 : 1 = 12 12 : 4 = 3
12 : 2 = 6 12 : 6 = 2
12 : 3 = 4 12 : 12 = 1
Luyện tập, vận dụng 3: Tìm tất cả các số có hai chữ số là ước chung của a và b, biết rằng ƯCLN(a, b) = 80.
Lời giải:
- Ước của 80 có 2 chữ số là: 10; 16;20;40;80. Vì ước chung của a và b đều là ước của ƯCLN(a, b) = 80 nên tất cả các số có hai chữ số là ước chung của a và b là: 10, 16, 20, 40, 80.
II. Tìm ước chung lớn nhất bằng cách phân tích các số ra thừa số nguyên tố
Hoạt động 3: Ta có thể tìm ƯCLN (36, 48) theo các bước sau:
Bước 1. Phân tích 36 và 48 ra thừa số nguyên tố
36 = 2 . 2 . 3 . 3 = 22 . 32
48 = 2 . 2 . 2 .2 . 3 = 24 . 3
Bước 2. Chọn ra các thừa số nguyên tố chung của 36 và 48 là 2 và 3.
Bước 3. Với mỗi thừa số nguyên tố chung 2 và 3, ta chọn lũy thừa với số mũ nhỏ nhất
+) Số mũ nhỏ nhất của 2 là 2, ta chọn 22.
+) Số mũ nhỏ nhất của 3 là 1, ta chọn 31.
Bước 4. Lấy tích của các lũy thừa đã chọn, ta nhận được ước chung lớn nhất cần tìm ƯCLN (36, 48) = 22 . 31 = 12.
Luyện tập, vận dụng 4: Tìm ƯCLN của 126 và 162.
Lời giải:
126 = 2.7.3
162 = 2
=> ƯCLN{126;162} = 2. 3
III. Hai nguyên tố cùng nhau
Hoạt động 4: Tìm ƯCLN(8, 27).
Lời giải:
Ta có: 8 = 2 . 4 = 2 . 2. 2 = 23
27 = 3 . 9 = 3 . 3. 3 = 33
Ta thấy hai số 8 và 27 không có thừa số nguyên tố chung do đó ƯCLN của chúng bằng 1.
Vậy ƯCLN(8, 27) = 1.
Luyện tập, vận dụng 5: Hai số 24 và 35 có nguyên tố cùng nhau không? Vì sao?
Lời giải:
- Hai số 24 và 35 là hai số nguyên tố cùng nhau vì ƯCLN(24,35) = 1
Hoạt động 5:
a) Tìm ƯCLN(4, 9).
b) Có thể rút gọn phân số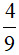 
được nữa hay không?
Lời giải:
a) 4 = 2
ƯCLN(4, 9) = 1.
b) Không thể rút gọn phân số
Bài tập
Bài tập 1: Số 1 có phải là ước chung của hai số tự nhiên bất kì không? Vì sao?
Lời giải:
Số 1 là ước chung của hai số tự nhiên bất kì vì tất cả các số tự nhiên đều có ước là 1.
Bài tập 2: Quan sát hai thanh sau:
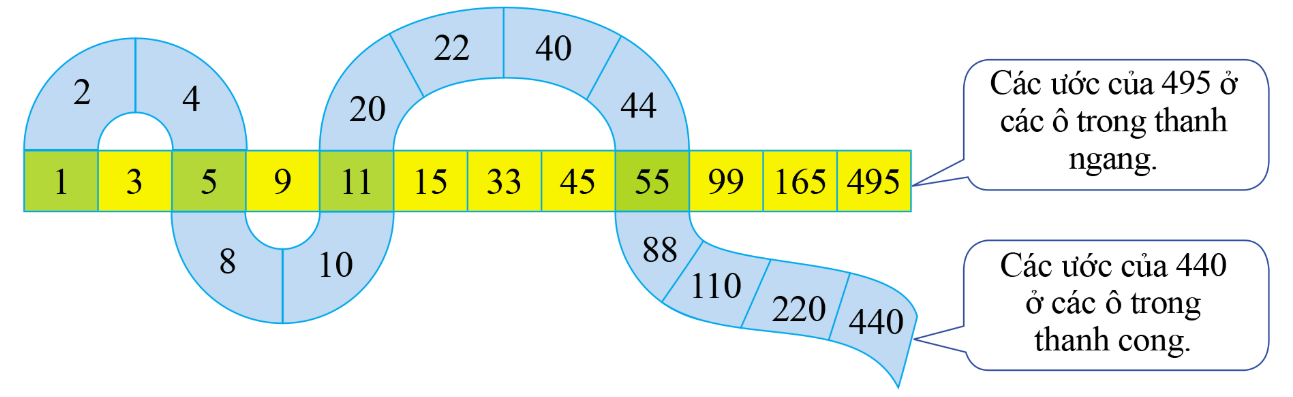
a) Viết tập hợp ƯC(440, 495).
b) Tìm ƯCLN(440, 495).
Lời giải:
a) Các ô nằm trên cả 2 thanh là 1;5;11;55 nên ƯC(440,495) = {1;5;11;55}
b) ƯCLN(440,495) = 55.
Bài tập 3: Tìm ước chung lớn nhất của từng cặp số trong ba số sau đây:
a) 31, 22, 34;
b) 105, 128, 135;
Lời giải:
a) 31 = 1 . 31; 22 = 2 . 11; 34 = 2 . 17
ƯCLN(31,22) = 1
ƯCLN(31,34) = 1
ƯCLN (22,34) = 2
b) 105 = 3 . 5 . 7; 128 = 2
ƯCLN (105,128) = 1
ƯCLN (128,135) = 1
ƯCLN (105,135) = 15
Bài tập 4: Tìm ƯCLN(126, 150). Từ đó hãy tìm tất cả các ước chung của 126 và 150.
Lời giải:
Do đó: 126 = 2 . 3 . 3 . 7 = 2 . 32 . 7
150 = 2 . 3 . 5 . 5 = 2 . 3 . 52
Các thừa số nguyên tố chung của 126 và 150 là 2 và 3
Số 2 có số mũ nhỏ nhất là 1; số 3 có số mũ nhỏ nhất là 1.
Do đó: ƯCLN(126, 150) = 21 . 31 = 2 . 3 = 6
Lại có 6 có các ước là 1; 2; 3; 6
Ước chung của 126 và 150 là ước của ƯCLN(126, 150) là 1; 2; 3; 6
Hay ƯC(126, 150) = {1; 2; 3; 6}
Vậy ƯCLN(126, 150) = 6; ƯC(126, 150) = {1; 2; 3; 6}.
Bài tập 5: Rút gọn các phân số sau về phân số tối giản: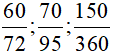 
.
Lời giải:
Bài tập 6: Phân số 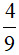bằng các phân số nào trong các phân số sau: 
?
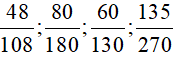Lời giải:
Ta thấy các phân số 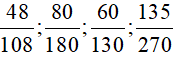chưa là phân số tối giản, mà phân số 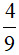là phân số tối giản (vì 4 và 9 là hai số nguyên tố cùng nhau) nên ta đi rút gọn các phân số 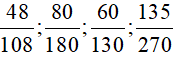rồi so sánh.
+ Ta có: 48 = 3 . 16 = 3 . 24; 108 = 4 . 27 = 22 . 33
Các thừa số nguyên tố chung là 2, 3 và số mũ nhỏ nhất của 2 là 2; số mũ nhỏ nhất của 3 là 1.
Nên ƯCLN(48, 108) = 22 . 3 = 12.
Do đó: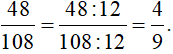 
+ Ta có: 80 = 8 . 10 = 23 . (2 . 5) = 24 . 5
180 = 10 . 18 = (2 . 5) .(2 . 3 . 3) = 22 . 32 . 5
Các thừa số nguyên tố chung là 2 và 5; Số 2 có số mũ nhỏ nhất là 2, số 5 có số mũ nhỏ nhất là 1.
Nên ƯCLN(80, 180) = 22 . 5 = 20
Do đó: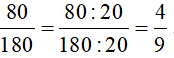 
+ Ta có: 60 = 6 . 10 = (2. 3) . (2 . 5) = 22 . 3 . 5
130 = 10 . 13 = 2 . 5 . 13
Các thừa số nguyên tố chung là 2 và 5, số 2 và số 5 đều có số mũ nhỏ nhất là 1.
Nên ƯCLN(60, 130) = 2 . 5 = 10
Do đó: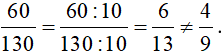 
.
+ Ta có: 135 = 5 . 27 = 5 . 33; 270 = 10 . 27 = (2 . 5) .33 = 2 . 33 . 5
Các thừa số nguyên tố chung là 3 và 5. Số 3 có số mũ nhỏ nhất là 3 và 5 có số mũ nhỏ nhất là 1.
Nên ƯCLN(135, 270) = 33. 5 = 135
Do đó: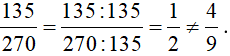 
.
Vậy trong các phân số đã cho, các phân số bằng 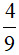là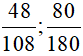 
Bài tập 7: Một nhóm gồm 24 bạn nữ và 30 bạn nam tham gia một số trò chơi. Có thể chia các bạn thành nhiều nhất bao nhiêu đội chơi sao cho số bạn nam cũng như số bạn nữ được chia đều vào các đội?
Lời giải:
Gọi a là số đội được chia
Khi đó: a là ước chung lớn nhất của 24 và 36
Ta có: ƯC(24,30) = {1,2,3 ,6}
=> ƯCLN (24,30) = 6
Vậy có thể chia các bạn thành nhiều nhất 6 đội.
Bài tập 8: Một khu đất có dạng hình chữ nhật với chiều dài 48m, chiều rộng 42m. Người ta muốn chia khu đất ấy thành những mảnh hình vuông bằng nhau (với độ dài cạnh đo theo đơn vị mét là số tự nhiên) để trồng các loại rau. Có thể chia được bằng bao nhiêu cách? Với cách chia nào thì cạnh của mảnh đất hình vuông là lớn nhất và bằng bao nhiêu?
Lời giải:
Để chia khu đất thành những mảnh hình vuông bằng nhau thì 48 và 42 phải chia hết cho độ dài cạnh hình vuông. Tức là cạnh hình vuông là ước chung của 48 và 42.
Ta có: ƯC(42,48) = {1;2;3;6}.
Do đó 48 và 42 có 4 ước chung nên có 4 cách chia.
Ta thấy 6 là ước chung lớn nhất của 42 và 48 nên ƯCLN(42, 48) = 6 nên cạnh của mảnh đất hình vuông lớn nhất có thể chia là 6m.
Vậy:
+ Số cách chia thành những mảnh hình vuông bằng nhau là 4 cách.
+ Với cách chia độ dài là 6m thì cạnh của mảnh đất hình vuông là lớn nhất.