I. Hình có tâm đối xứng
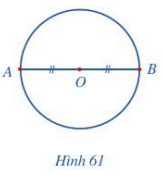
Hoạt động 1: Quan sát đường kính AB của đường tròn tâm O (Hình 61)
- Vì điểm O là trung điểm đoạn thẳng AB nên ta nói hai điểm A và B đối xứng với nhau qua tâm O.
- Đường tròn tâm O là hình có tâm đối xứng và tâm đối xứng chính là tâm O của đường tròn.
Hoạt động 2: Lấy bốn chiếc ê ke giống nhau để xếp thành hình như Hình 62.
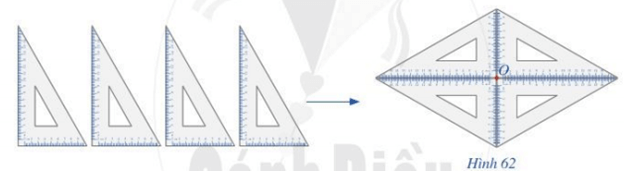
Hình 61 hay hình nhận được ở Hình 62 gọi là hình có tâm đối xứng và điểm O được gọi là tâm đối xứng của hình.
II. Tâm đối xứng của một số hình
Luyện tập, vận dụng: Trong thực tế, có nhiều hình có tâm đối xứng. Chẳng hạn:
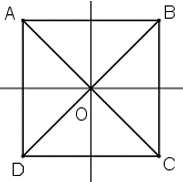
+) Hình vuông có tâm đối xứng là giao hai đường chéo (điểm O trong hình vẽ).
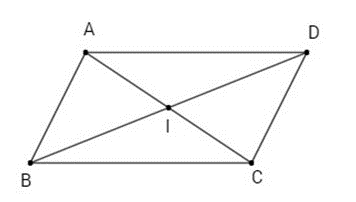
+) Hình bình hành có tâm đối xứng và tâm đối xứng của hình bình hành là giao điểm hai đường chéo của hình bình hành (điểm I trong hình vẽ).
Bài tập
Bài tập 1: Trong các hình từ Hình 66 đến Hình 69, hình nào có tâm đối xứng? Nếu là hình có tâm đối xứng, hãy chỉ ra tâm đối xứng của hình đó.

Lời giải:
Tất cả các hình trên, từ Hình 66 đến Hình 69 đều có tâm đối xứng như sau:
+) Hình 66: (chấm đỏ trên hình)
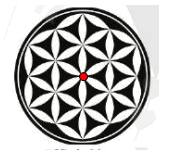
+) Hình 67: (chấm đỏ trên hình)
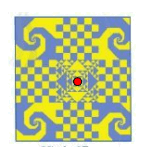
+) Hình 68: (chấm đỏ trên hình)

+) Hình 69: (chấm đen trên hình)
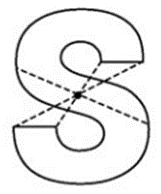
Bài tập 2: Trong Hình 70, các hình từ a) đến c), hình nào có tâm đối xứng? Nếu là hình có tâm đối xứng, hãy chỉ ra tâm đối xứng của hình đó (kể cả màu sắc)

Lời giải:

- Hình a và b có tâm đối xứng.
- Hình c không có tâm đối xứng.
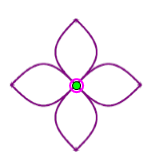
Bài tập 3: Hãy tìm một số hình có tâm đối xứng trong thực tiễn.
Lời giải:
+) Hình biển báo giao thông:

+) Hình bông hoa:
+) Hình viên gạch hoa:

