Câu hỏi khởi động: Ta đã biết 3 . 2 = 6. Phải chăng (– 3) . (– 2) = – 6?
Lời giải:
Nhận thấy phép tính (– 3) . (– 2) là phép nhân hai số nguyên âm. Để làm được phép nhân này, ta phải học qua §5.
Sau khi học bày này, ta thực hiện ngay phép nhân hai số nguyên:
(– 3) . (– 2) = 3 . 2 = 6
Vì 6 và – 6 khác nhau. Do đó phát biểu trên đề bài là không chính xác.
I. Phép nhân hai số nguyên khác dấu
Hoạt động 1:
a) Hoàn thành phép tính: (– 3) . 4 = (– 3) + (– 3) + (– 3) + (– 3) = (?).
b) So sánh (– 3). 4 và – (3. 4).
Lời giải:
a) (- 3) . 4 = (- 3) + (- 3) + (- 3) + (- 3) = - 12
b) – (3 . 4) = - (12)
Vậy (- 3) . 4 = – (3 . 4)
Luyện tập, vận dụng 1: Tính:
a) (– 7) . 5;
b) 11 . (– 13).
Lời giải:
a) (- 7) . 5 = - (7 . 5) = - 35
b) 11 . (- 13) = - (11 . 13) = - 143
II. Phép nhân hai số nguyên cùng dấu
Hoạt động 2:
a) Quan sát kết quả của ba tích đầu, ở đó mỗi lần ta giảm 1 đơn vị ở thừa số thứ hai. Tìm kết quả của hai tích cuối.
(– 3) . 2 = – 6
(– 3) . 1 = – 3 tăng 3 đơn vị
(– 3) . 0 = 0 tăng 3 đơn vị
(– 3) . (–1) = (?1) tăng 3 đơn vị
(– 3) . (– 2) = (?2) tăng 3 đơn vị
b) So sánh (– 3). (– 2) và 3. 2.
Lời giải:
a) Số cần điền ở (?1) là 3 (do tăng 3 đơn vị nên ta lấy 0 + 3 = 3)
Tương tự, số cần điền ở (?2) là 6 (vì 3 + 3 = 6)
Vậy ta đã tìm được kết quả hai tích cuối lần lượt là 3 và 6.
b) Theo câu a ta có: (– 3) . (– 2) = 6
Lại có: 3 . 2 = 6
Do đó: (– 3) . (– 2) = 3 . 2
Luyện tập, vận dụng 2: Tính giá trị của biểu thức trong mỗi trường hợp sau:
a) – 6x – 12 với x = – 2;
b) – 4y + 20 với y = – 8.
Lời giải:
a) Thay x = - 2 => - 6 . (- 2) – 12 = 12 – 12 = 0
b) Thay y = - 8 => - 4 . (- 8) + 20 = 32 + 20 = 52
III. Tính chất của phép nhân các số nguyên
Hoạt động 3: Tính và so sánh kết quả:
a) (– 4) . 7 và 7 . (– 4);
b) [(– 3). 4] . (– 5) và (– 3) . [4. (– 5)];
c) (– 4) . 1 và – 4;
d) (– 4) . (7 + 3) và (– 4) . 7 + (– 4) . 3.
Lời giải:
a) (- 4) . 7 = - (4 . 7) = - 28
7 . (- 4) = - (7 . 4) = - 28
Vậy (- 4) . 7 = 7 . (- 4)
b) [(- 3) . 4] . (- 5) = (- 12) . (- 5) = 12 . 5 = 60
(- 3) . [4 . (- 5)] = (- 3) . (- 20) = 3 . 20 = 60
Vậy [(- 3) . 4] . (- 5) = (- 3) . [4 . (- 5)]
c) (- 4) . 1 = - (4 . 1) = - 4
d) (- 4) . (7 + 3) = (- 4) . (10) = - 40
(- 4) . 7 + 7 . (- 4) . 3 = - (4 . 7) + [- (4 . 3)] = - 28 + (- 12) = - 40
Vậy (- 4) . (7 + 3) = (- 4) . 7 + 7 + (- 4) . 3
Luyện tập, vận dụng 3: Tính một cách hợp lí:
a) (– 6) . (– 3) . (– 5);
b) 41 . 81 – 41. (– 19).
Lời giải:
a) (– 6) . (– 3) . (– 5)
= [(–6) . (– 5)] . (– 3) (tính chất giao hoán và kết hợp)
= 30 . (– 3)
= – 90.
b) 41 . 81 – 41 . (– 19)
= 41 . [81 – (– 19)] (tính chất phân phối của phép nhân đối với phép trừ)
= 41 . (81 + 19)
= 41 . 100
= 4 100.
Bài tập
Bài tập 1: Tính:
a) 21 . (– 3);
b) (– 16) . 5;
c) 12 . 20;
d) (– 21) . (– 6).
Lời giải:
a) 21 . (- 3) = - (21 . 3) = - 63
b) (- 16 ) . 5 = - (16 . 5) = - 80
c) 12 . 20 = 240
d) (- 21) . (- 6) = 126
Bài tập 2: Tìm số thích hợp ở (?):

Lời giải:
Ta có: 15 . 6 = 90
(– 3) . 14 = – (3 . 14) = – 42
11 . (– 23) = – (23 . 11) = – 253
(– 4) . (– 125) = 4 . 125 = 500
Có: 21 = 7 . 3 nên 21 . (– 1) = 7 . 3 . (– 1) hay – 21 = 7 . (– 3)
72 = 9 . 8 = (– 9) . (– 8)
Khi đó các số thích hợp được điền vào bảng như sau:

Bài tập 3: Tính:
a) 1010 . (– 104),
b) (– 2) . (– 2) . (– 2) . (– 2) . (– 2) + 25;
c) (– 3) . (– 3) . (– 3) . (– 3) – 34.
Lời giải:
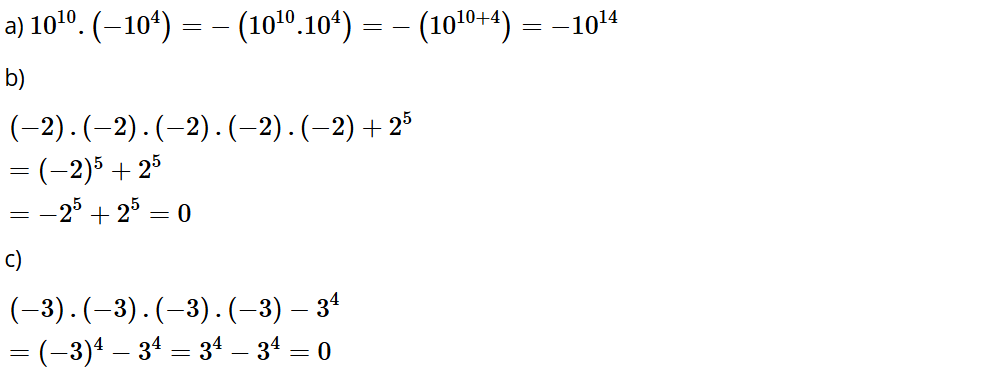
Bài tập 4: Tính 8. 25. Từ đó suy ra kết quả của các phép tính sau:
a) (– 8) . 25;
b) 8 . (– 25);
c) (– 8) . (– 25).
Lời giải:
Ta có: 8 . 25 = 200
=> a) (- 8) . 25 = - 200.
b) 8 . (- 25) = - 200.
c) (- 8) . (- 25) = 200.
Bài tập 5: Tính giá trị của biểu thức trong mỗi trường hợp sau:
a) 2x, biết x = – 8;
b) – 7y, biết y = 6;
c) – 8z – 15, biết z = – 4.
Lời giải:
a) Với x = – 8 thì ta có:
2x = 2 . (– 8) = – (2 . 8) = – 16.
b) Với y = 6 thì ta có:
– 7y = (– 7) . 6 = – (7 . 6) = – 42.
c) Với z = – 4 thì ta có:
– 8z – 15 = (– 8) . (– 4) – 15 = 8 . 4 – 15 = 32 – 15 = 17.
Bài tập 6: Xác định các dấu “ < “, “>” thích hợp cho (?):
a) 3 . (– 5)  0;
0;
b) (– 3) . (– 7)  0;
0;
c) (– 6) . 7  (– 5) . (– 2).
(– 5) . (– 2).
Lời giải:
a) 3 . (- 5) < 0
b) (- 3) . (- 7) > 0
c) (- 6) . 7 < (- 5) . (- 2)
Bài tập 7: Tính một cách hợp lí:
a) (– 16) . (– 7) . 5;
b) 11. (– 12) + 11. (– 18);
c) 87. (– 19) – 37 . (– 19);
d) 41 . 81 .(– 451). 0.
Lời giải:
a) (– 16) . (– 7) . 5
= [(– 16) . 5] . (– 7) (tính chất giao hoán và kết hợp)
= [– (16 . 5)] . (– 7)
= (– 80) . (– 7)
= 80 . 7
= 560.
b) 11 . (– 12) + 11 . (– 18)
= 11 . [(– 12) + (– 18)] (tính chất phân phối của phép nhân đối với phép cộng)
= 11 . [– (12 + 18)]
= 11 . (– 30)
= – (11 . 30)
= – 330.
c) 87 . (– 19) – 37 . (– 19)
= (– 19) . (87 – 37) (tính chất phân phối của phép nhân đối với phép trừ)
= (– 19) . 50
= – (19 . 50)
= – 950.
d) 41 . 81 . (– 451) . 0 = 0. (tính chất phép nhân một số với 0)
Hoặc chúng ta có thể làm lần lượt từng bước như sau:
41 . 81 . (– 451) . 0
= 41 . 81 . [(– 451) . 0] (tính chất kết hợp)
= 41 . 81 . 0 (tính chất phép nhân một số với 0)
= 41 . (81 . 0) (tính chất kết hợp)
= 41 . 0 = 0. (tính chất phép nhân một số với 0)
Bài tập 8: Chọn từ “âm”, “dương” thích hợp cho (?)
a) Tích ba số nguyên âm là một số nguyên (?);
b) Tích hai số nguyên âm với một số nguyên dương là một số nguyên (?);
c) Tích của một số chẵn các số nguyên âm là một số nguyên (?);
d) Tích của một số lẻ các số nguyên âm là một số nguyên (?).
Lời giải:
a) Tích ba số nguyên âm là một số nguyên âm.
b) Tích hai số nguyên âm với một số nguyên dương là một số nguyên dương.
c) Tích của một số chẵn các số nguyên âm là một số nguyên dương.
d) Tích của một số lẻ các số nguyên âm là một số nguyên âm.
Bài tập 9: Công ty Ánh Dương có lợi nhuận ở mỗi tháng trong Quý I là – 30 triệu đồng. Trong Quý II, lợi nhuận mỗi tháng của công ty là 70 triệu đồng. Sau 6 tháng đầu năm, lợi nhuận của công ty Ánh Dương là bao nhiêu tiền?
Lời giải:
* Lợi nhuận Quý I = (- 30) . 3 = - 90 triệu đồng.
* Lợi nhuận Quý II = 70 . 3 = 210 triệu đồng.
Sau 6 tháng đầu năm, lợi nhuận của công ty Ánh Dương là: (- 90) + 210 = 120 triệu đồng.
Bài tập 10: Sử dụng máy tính cầm tay
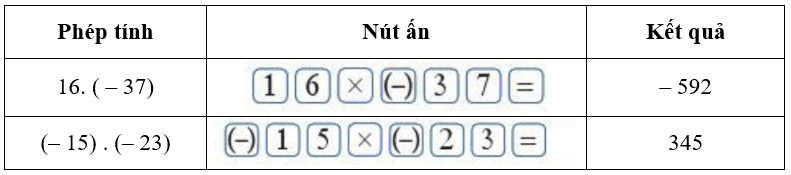
Dùng máy tính cầm tay để tính:
23 . (– 49);
(– 215) . 207;
(– 124) . (– 1 023).
Lời giải:
Sử dụng máy tính bỏ túi, ta tính được:
23 . (– 49) = – 1 127;
(– 215) . 207 = – 44 505;
(– 124) . (– 1 023) = 126 852.
