Giải SGK Toán 6 Cánh Diều Bài 5: Phép tính lũy thừa với số mũ tự nhiên

Câu hỏi khởi động: Vi khuẩn E.coli trong điều kiện nuôi cấy thích hợp cứ 20 phút lại phân đôi một lần

(Nguồn: sinh học 10, NXB Giáo dục Việt Nam, 2010)

Giả sử lúc đầu có 1 vi khuẩn. Sau 120 phút có bao nhiêu vi khuẩn?

Lời giải:

+) Trước khi chưa học bài Lũy thừa, em giải quyết bài toán trên như sau: 

Vì cứ sau 20 phút, vi khuẩn lại phân đôi 1 lần nên sau 20 phút đầu, từ 1 vi khuẩn ta có 2 vi khuẩn.

Sau 20 phút tiếp theo (tức là sau 40 phút), từ 2 vi khuẩn phân đôi thành 2 . 2 = 4 vi khuẩn.

Sau 20 phút tiếp (tức là sau 60 phút), từ 4 vi khuẩn phân đôi thành 4 . 2 = 8 vi khuẩn.

Sau 20 phút tiếp (tức là sau 80 phút), từ 8 vi khuẩn phân đôi thành 8 . 2 = 16 vi khuẩn.

Tiếp tục sau 20 phút nữa (tức là sau 100 phút), từ 16 vi khuẩn phân đôi thành 16 . 2 = 32 vi khuẩn.

Sau 20 phút nữa (tức là sau 120 phút), từ 32 vi khuẩn phân đôi thành 32 . 2 = 64 vi khuẩn. 

Vậy sau 120 phút có tất cả 64 vi khuẩn. 

+) Sau khi học xong bài Lũy thừa, em có thể giải quyết bài toán như sau: 

120 phút hơn 20 phút số lần là: 120 : 20 = 6 (lần)

Cứ sau 20 phút, vi khuẩn lại phân đôi 1 lần, tức là gấp 2 lần số lượng ban đầu. 

Vậy sau 120 phút, có tất cả: 26 = 64 vi khuẩn.

I. Phép nhân lên lũy thừa

Hoạt động 1: Người ta viết gọn tổng của nhiều số hạng bằng nhau thành phép nhân, chẳng hạn: 2 + 2 + 2 + 2 + 2 + 2 = 2.6.

Ta cũng có thể viết gọn tích của nhiều thừa số bằng nhau, chẳng hạn: 2.2.2.2.2.2 được viết gọn

Lời giải:

Ta cũng có thể viết gọn tích của nhiều thừa số bằng nhau, chẳng hạn:

2 . 2 . 2 . 2 . 2 . 2 được viết gọn là 26. Số 2 gọi là cơ số và số 6 gọi là số mũ.

Ta có : 26 = 64

Luyện tập, vận dụng 1: Viết và tính các lũy thừa sau:

a) Năm mũ hai;

b) Hai lũy thừa bảy;

c) Lũy thừa bậc ba của sáu.

Lời giải:

a) 52 = 5 . 5 =  25

b) 27 = 2 . 2 . 2 . 2 . 2 . 2 . 2 = 128   

c) 63 = 6 .6 . 6 = 216

Luyện tập, vận dụng 2: Viết các số sau dưới dạng lũy thừa với cơ số cho trước:

a) 25, cơ số 5;

b) 64, cơ số 4.

Lời giải:

a) Để viết số 25 dưới dạng lũy thừa với cơ số 5, ta tách số 25 thành tích với các thừa số là 5 rồi đưa về dạng lũy thừa: 

25 = 5 . 5 = 52. 

Vậy 25 = 52.

b) Để viết số 64 dưới dạng lũy thừa với cơ số 4, ta tách số 64 thành tích với các thừa số là 4 rồi đưa về dạng lũy thừa:

64 = 4 . 16 = 4 . (4 . 4) = 4 . 4 . 4 = 43.  

Vậy 64 = 43. 

II. Nhân hai lũy thừa cùng cơ số

Hoạt động 2: So sánh: 23.24 và  27.

Lời giải:

Luyện tập, vận dụng 3: Viết kết quả mỗi phép tính sau dưới dạng một lũy thừa:

a) 25 . 64 ; 

b) 20 . 5 . 103.  

Lời giải:

a) Trước tiên ta viết 64 dưới dạng lũy thừa cơ số 2:

Ta có: 64 = 2 . 32 = 2 . 2 . 16 = 2 . 2 . 2 . 8 = 2 . 2 . 2 . 2 . 2 . 2 = 26

Do đó: 25 . 64 = 25 . 26 = 25+6 = 211. 

b) Ta có: 20 . 5 . 103 = 100 . 103 = 10 . 10 . 103 = 102 . 103 = 102+3 = 105. 

III. Chia hai lũy thừa cùng cơ số

Hoạt động 3: So sánh:25 : 23 và 22.

Lời giải:

Luyện tập, vận dụng 4: Viết kết quả mỗi phép tính sau dưới dạng một lũy thừa:

a) 65 : 6 ; 

b)  1288 : 23. 

Lời giải:

a) 65 : 6 = 65 : 61 = 65−1 = 64

b) 128 : 23 = 27 : 23 = 27−3 = 24

Bài tập

Bài tập 1: Viết các tích sau dưới dạng lũy thừa:

a) 5 . 5 . 5 . 5;

b) 9 . 9 . 9 . 9 . 9 . 9 . 9;

c) 7 . 7 . 7 . 7 . 7;

d) a . a . a . a . a . a . a . a.

Lời giải:

a) 5 . 5. 5 . 5 = 54. (vì trong tích có 4 thừa số 5)

b) 9 . 9 . 9 . 9 . 9 . 9 . 9 = 97. (vì trong tích có 7 thừa số 9)

c) 7 . 7 . 7 . 7 . 7 = 75. (vì trong tích có 5 thừa số 7)

d) a . a . a . a . a . a . a . a = a8. (vì trong tích có 8 thừa số a)

Bài tập 2: Xác định cơ số, số mũ và tính mỗi lũy thừa sau: 25, 52, 92, 110, 101

Lời giải:

25: cơ số 2, số mũ 5 và 25 = 2 . 2 . 2 . 2 . 2 = 32

52: cơ số 5, số mũ 2 và 52 = 5 . 5 = 25

92: cơ số 9, số mũ 2 và 92 = 9 . 9 = 81

110: cơ số 1, số mũ 10 và 110 = 1

101: cơ số 10, số mũ 1 và 101 = 10

Bài tập 3: Viết các số sau dưới dạng lũy thừa với cơ số cho trước:

a) 81, cơ số 3;

b) 81, cơ số 9;

c) 64, có số 2;

d) 100 000 000, cơ số 10.

Lời giải:

Bài tập 4: Viết kết quả mỗi phép tính sau dưới dạng một lũy thừa:

a)  34.35 ; 16.29  ;  16.32 ; 

b)  128 : 12 ; 243 : 34  ;  109 : 10000 ; 

c)  4.86.2.83 ;  122.2.123.6  ;  63.2.64.3 . 

Lời giải:

a) +) 34. 35 = 34 + 5 = 39. 

+) 16 . 29 = (2 . 2 . 2 . 2) . 29 = 24 . 29 = 24 + 9 = 213.

+) 16 . 32 = 24 . (2 . 2 . 2 . 2 . 2) = 24 . 25 = 24 + 5 = 29.

b) +) 128 : 12 = 128 : 121 = 128 - 1 = 127.

+) 243 : 34 = (3. 81) : 34 = (3 . 3 . 27) : 34 = (3 . 3 . 3 . 3. 3) : 34 = 35 : 34 = 35 - 4 =31.

+) 109 : 10 000 = 109 : (10 . 1 000) = 109 : (10. 10 . 100) 

= 109 : (10 . 10 . 10 . 10) 

= 109 : 104 = 109 - 4  = 105.

c) +) 4. 86 . 2 . 83 

= 4 . 2 . 86 . 83 (tính chất giao hoán) 

= (4 . 2) . 86 . 83 (tính chất kết hợp)

= 8 .  86 . 83 

= 81 . 86 . 83 

= 81 + 6 . 83 

= 87 . 83 = 87 + 3 = 810. 

+) 122 . 2 . 123 . 6 

= (2. 6) . (122 . 123)  (tính chất giao hoán và kết hợp)

= 12 . 122 + 3 

= 121 . 125 = 121 + 5  = 126. 

+) 63 . 2 . 64 . 3 

= (2 . 3) . (63 . 64) (tính chất giao hoán và kết hợp)

= 6 . 63 + 4 

= 61 . 67 = 61 + 7 = 68. 

Bài tập 5: So sánh:

a) 32 và 3 . 2;

b) 23 và 32 ; 

c) 33 và 34 . 

Lời giải:

a) 32 và 3.2;

32 = 3 . 3 = 9 và 3 . 2 = 6

Vì 9 > 6 => 32 > 3.

b) 23 và 32;   

  23 = 2 . 2 . 2 = 8 và 32 = 3 . 3 = 9;   

Vì 8 < 9 => 23 < 32;   

c) 32 và 34

32 = 3 . 3  và 34 = 3 . 3 . 3 . 3 . 3 

Vì 2 < 4 => 32 < 34

Bài tập 6: Khối lượng của Mặt Trời khoảng 1 988 550 . 1021 tấn, khối lượng của Trái Đất khoảng 6.1021 tấn. (Nguồn: http://nssdc.gsfc.nasa.gov). Khối lượng của Mặt Trời gấp khoảng bao nhiêu lần khối lượng của Trái Đất?

Lời giải:

Bài tập 7: Đố. Cho biết 112 = 121; 1112 =12 321. Hãy dự đoán 11112 bằng bao nhiêu. Kiểm tra lại dự đoán đó.

Lời giải:

Ta có:  112 = 121; 1112 = 12 321

Do đó ta dự đoán: 1 1112 = 1 234 321

Kiểm tra: 1 1112 = 1 111 . 1 111  

Ta có: 

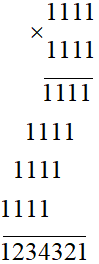
Vậy 1 1112 = 1 234 321.