Giải SGK Toán 11 Cánh Diều Bài 2: Giới hạn của hàm số

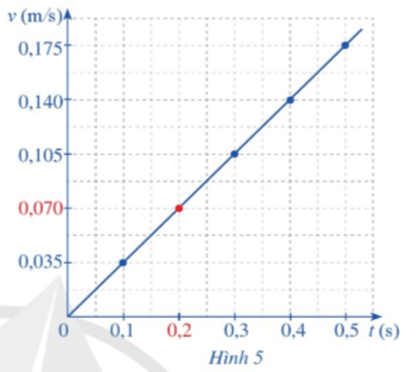
Câu hỏi khởi động: Hình 5 biểu diễn đồ thị hàm số vận tốc theo biến số t (t là thời gian, đơn vị: giây). Khi các giá trị của biến số t dần tới 0,2 (s) thì các giá trị tương ứng của hàm số v(t) dần tới 0,070 (m/s)..

Trong toán học, giá trị 0,070 biểu thị khái niệm gì của hàm số v(t) khi các giá trị của biến số t dần tới 0,2?

Trả lời:

- Trong toán học giá trị 0,070 được gọi là giới hạn của hàm số khi x tiến tới 0,2.

I. Giới hạn hữu hạn của hàm số tại một điểm

Hoạt động 1: Xét hàm số f(x) = 2x.

a) Xét dãy số (xn), với xn=1+1n . Hoàn thành bảng giá trị f(xn) tướng ứng.

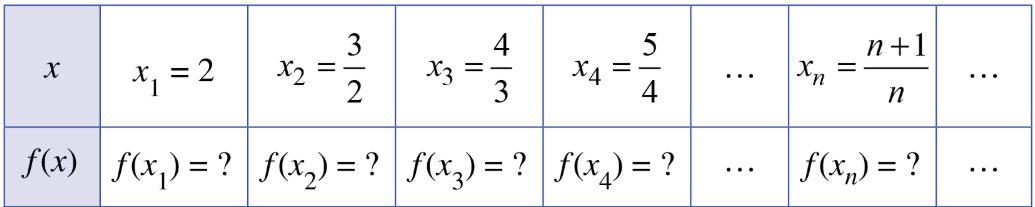
Các giá trị tương ứng của hàm số f(x1),f(x2),...,f(xn),... lập thành một dãy số mà ta kí hiệu là (f(xn)). Tìm limf(xn).

b) Chứng minh rằng với dãy số bất kì (xn),xn→1 ta luôn có f(xn) → 2.

Trả lời:

Ta có bảng giá trị sau:

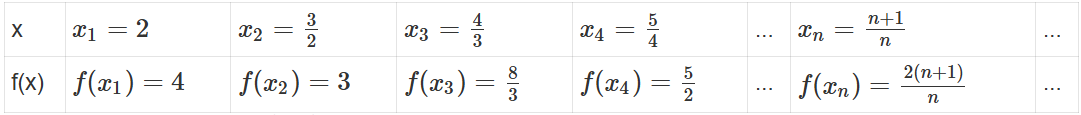
Ta có: limf(xn)=lim2(n+1)n=2

b) Lấy dãy (xn) bất kí thỏa mãn xn → 1 ta có:

f(xn)=2xn

⇒ limf(xn)=lim2xn=2limxn=2.1=2

Luyện tập, vận dụng 1: Sử dụng định nghĩa, chứng minh rằng: $\underset{x\to 2}{\mathrm{li}\text{m}}{\text{x}}^2$=4.

Trả lời:

Đặt f(x) = x2

Giả sử (xn) là dãy số thỏa mãn limxn = 2.

⇒ limf(xn) = lim$x_n^2=2^2$=4.

Vậy $\underset{x\to 2}{li\text{m}}{\text{x}}^2$=4.

Hoạt động 2: Cho hàm số f(x) = x2 – 1, g(x) = x + 1.

a) limx→1f(x) và limx→1g(x)

b) limx→1(f(x)+g(x)) và so sánh với limx→1f(x)+limx→1g(x)

c) limx→1(f(x)−g(x)) và so sánh với limx→1f(x)−limx→1g(x)

d) limx→1(f(x).g(x)) và so sánh với limx→1f(x).limx→1g(x)

e) limx→1f(x)g(x) và so sánh với limx→1f(x)limx→1g(x)

Trả lời:

a) Giả sử (xn) là dãy số bất kì thỏa mãn limxn = 1. Khi đó ta có:

limf(xn)=lim(x2n−1)=limx2n−1=1−1=0

⇒ limf(x) = 0.

limg(xn)=lim(xn+1)=limxn+1=2

⇒ limg(x) = 2.

b) Ta có: f(x)+g(x)=x2–1+x+1=x2+x

(xn) là dãy số bất kì thỏa mãn limxn = 1. Khi đó ta có:

lim(f(xn)+g(xn))=lim(x2n+xn)=limx2n+limxn=12+1=2

⇒limx→1(f(x)+g(x))=2

Ta lại có: limx→1f(x)+limx→1g(x)=0+2=2

Vậy limx→1(f(x)+g(x))=limx→1f(x)+limx→1g(x)=2

c) Ta có: f(x)–g(x)=x2–1–x–1=x2–x–2

(xn) là dãy số bất kì thỏa mãn limxn = 1. Khi đó ta có:

lim(f(xn)−g(xn))=lim(x2n−xn−2)=limx2n−limxn−2=12−1−2=−2

⇒limx→1(f(x)−g(x))=−2

Ta lại có: limx→1f(x)−limx→1g(x)=0−2=−2

Vậy limx→1(f(x)−g(x))=limx→1f(x)−limx→1g(x)=−2

d) Ta có: f(x).g(x)=(x2–1)(x+1)=x3+x2–x–1

(xn) là dãy số bất kì thỏa mãn limxn = 1. Khi đó ta có:

lim(f(xn).g(xn))=lim(x3n+x2n−xn−1)

=limx3n+limx2n−limxn−1=13+12−1−1=0

⇒limx→1(f(x).g(x))=0

Ta lại có: limx→1f(x).limx→1g(x)=0.2=0

Vậy limx→1(f(x).g(x))=limx→1f(x).limx→1g(x)=0

e) Ta có: f(x)g(x)=x2−1x+1

(xn) là dãy số bất kì thỏa mãn limxn = 1. Khi đó ta có:

limf(xn)g(xn)=limx2n−1xn+1

=lim(xn−1)(xn+1)xn+1=lim(xn−1)=0

⇒limx→1f(x)g(x)=0

Ta lại có: limf(x)limg(x)=02=0

Vậy limx→1f(x)g(x)=limx→1f(x)limx→1g(x)

Luyện tập, vận dụng 2: Tính:

a) $\underset{x\to 2}{\lim }\left(\left(x+1\right)\left(x^2+2x\right)\right)$;

b) $\underset{x\to 2}{\lim }\sqrt{x^2+x+3}$.

Trả lời:

a) $\underset{x\to 2}{\lim }\left(\left(x+1\right)\left(x^2+2x\right)\right)=\underset{x\to 2}{\lim }\left(x+1\right).\underset{x\to 2}{\lim }\left(x^2+2x\right)$= 3.8 = 24.

b) $\underset{x\to 2}{\lim }\sqrt{x^2+x+3}=\sqrt{\underset{x\to 2}{\lim }\left(x^2+x+3\right)}$= 3.

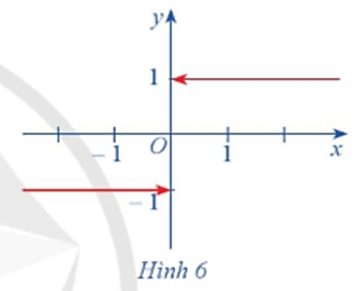
Hoạt động 3: Cho hàm số f(x) = 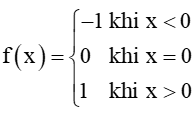. Hàm số f(x) có đồ thị ở Hình 6.

a) Xét dãy số (un) sao cho un < 0 và lim un = 0. Xác định f(un) và tìm lim f(un).

b) Xét dãy số (vn) sao cho vn > 0 và lim vn = 0. Xác định f(vn) và tìm limf(vn).

Trả lời:

a) Xét dãy số (un) sao cho un < 0 và lim un = 0. Khi đó f(un) = – 1 và lim f(un) = – 1.

b) Xét dãy số (vn) sao cho vn > 0 và lim vn = 0. Khi đó f(vn) = 1 và lim f(vn) = 1.

Luyện tập, vận dụng 3: Tính limx→−4+(x+4−−−−−√+x). 

Trả lời:

limx→−4+(x+4−−−−−√+x)=−4+4−−−−−−√−4=−4

II. Giới hạn hữu hạn của hàm số tại vô cực

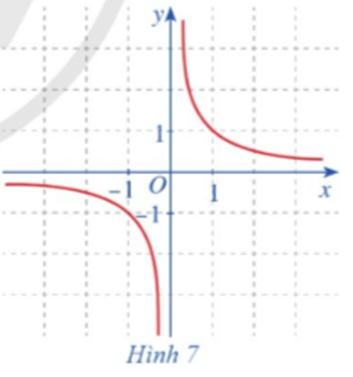
Hoạt động 4: Cho hàm số f(x) = $\frac{1}{x}$(x$\ne$0)có đồ thị như ở Hình 7. Quan sát đồ thị đó và cho biết:

a) Khi biến x dần tới dương vô cực thì f(x) dần tới giá trị nào.

b) Khi biến x dần tới âm vô cực thì f(x) dần tới giá trị nào.

Trả lời:

Dựa vào đồ thị ta thấy:

a) Hàm số f(x) tiến dần tới giá trị 0 khi x dần tới dương vô cực.

b) Hàm số tiến dần tới âm vô cực thì giá trị f(x) gần tới giá trị 0.

Luyện tập, vận dụng 4: Tính limx→−∞3x+24x−5. 

Trả lời:

limx→−∞3x+24x−5=limx→−∞3+2x4−5x=3+04−0=34

III. Giới hạn vô cực (một phía) của hàm số tại một điểm

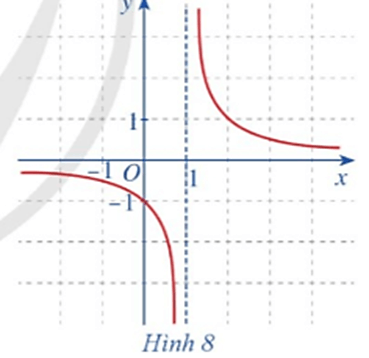
Hoạt động 5: Cho hàm số f(x) = $\frac{1}{x-1}\left(x\ne 1\right)$có đồ thị như Hình 8. Quan sát đồ thị đó và cho biết:

a) Khi biến x dần tới 1 về bên phải thì f(x) dần tới đâu.

b) Khi biến x dần tới 1 về bên trái thì f(x) dần tới đâu.

Trả lời:

a) Khi biến x dần tới 1 về bên phải thì f(x) dần tới +∞.

b) Khi biến x dần tới 1 về bên trái thì f(x) dần tới – ∞.

Luyện tập, vận dụng 5: Tính: limx→−2−1x+2. 

Trả lời:

limx→−2−1x+2=1−2+2=−∞

IV. Giới hạn vô cực của hàm số tại vô cực

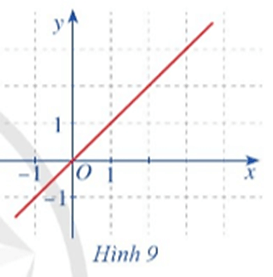
Hoạt động 6: Cho hàm số f(x) = x có đồ thị như Hình 9. Quan sát đồ thị đó và cho biết:

a) Khi biến x dần tới dương vô cực thì f(x) dần tới đâu.

b) Khi biến x dần tới âm vô cực thì f(x) dần tới đâu.

Trả lời:

Dựa vào đồ thị hàm số, ta thấy:

a) Khi biến x dần tới dương vô cực thì f(x) dần tới dương vô cùng.

b) Khi biến x dần tới âm vô cực thì f(x) dần tới âm vô cùng.

Luyện tập, vận dụng 6: Tính: limx→−∞x4. 

Trả lời:

limx→−∞x4=+∞

Bài tập

Bài tập 1: Sử dụng định nghĩa, tìm các giới hạn sau:

a) $\underset{x\to -3}{\lim }{x}^2$;

b) $\underset{x\to 5}{\lim }\frac{x^2-25}{x-5}$.

Trả lời:

a) $\underset{x\to -3}{\lim }{x}^2={\left(-3\right)}^2=9$

b) $\underset{x\to 5}{\lim }\frac{x^2-25}{x-5}=\underset{x\to 5}{\lim }\frac{\left(x-5\right)\left(x+5\right)}{x-5}=\underset{x\to 5}{\lim }$(x+5) = 10.

Bài tập 2: Biết rằng hàm số f(x) thỏa mãn limx→2−f(x)=3 và limx→2+f(x)=5. Trong trường hợp này có tồn tại giới hạn limx→2f(x) hay không? Giải thích. 

Trả lời:

Ta có: limx→2−f(x)≠limx→2+f(x)

Vậy không tồn tại giới hạn limx→2f(x). 

Bài tập 3: Tính các giới hạn sau:

a) $\underset{x\to 2}{\lim }$(x2-4x+3);

b) $\underset{x\to 3}{\lim }\frac{x^2-5x+6}{x-3}$;

c) $\underset{x\to 1}{\lim }\frac{\sqrt{x}-1}{x-1}$.

Trả lời:

a) $\underset{x\to 2}{\lim }$(x2-4x+3) = 22-4.2+3 = -1.

b) $\underset{x\to 3}{\lim }\frac{x^2-5x+6}{x-3}=\underset{x\to 3}{\lim }\frac{\left(x-3\right)\left(x-2\right)}{x-3}=\underset{x\to 3}{\lim }\left(x-2\right)=1$.

c) $\underset{x\to 1}{\lim }\frac{\sqrt{x}-1}{x-1}=\underset{x\to 1}{\lim }\frac{\sqrt{x}-1}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}=\underset{x\to 1}{\lim }\frac{1}{\sqrt{x}+1}=\frac{1}{2}$.

Bài tập 4: Tính các giới hạn sau:

a) limx→+∞9x+13x−4;

b) limx→−∞7x−112x+3;

c) limx→+∞x2+1√x;

d) limx→−∞x2+1√x;

e) limx→6−1x−6; 

g) limx→7+1x−7. 

Trả lời:

a) limx→+∞9x+13x−4=limx→+∞9+1x3−4x=3;

b) limx→−∞7x−112x+3=limx→−∞7−11x2+3x=72;

c) limx→+∞x2+1√x=limx→+∞x1+1x2√x=1;

d) limx→−∞x2+1√x=limx→−∞x1+1x2√x=1;

e) limx→6−1x−6=−∞;

g) limx→7+1x−7=+∞. 

Bài tập 5: Một công ty sản xuất máy tính đã xác định được rằng, trung bình một nhân viên có thể lắp ráp được N(t) = $\frac{50t}{t+4}\left(t\ge 0\right)$bộ phận mỗi ngày sau t ngày đào tạo. Tính $\underset{t\to +\infty }{\lim }$N(t)và cho biết ý nghĩa của kết quả.

Trả lời:

Ta có: $\underset{t\to +\infty }{\lim }N\left(t\right)=\underset{t\to +\infty }{\lim }\frac{50t}{t+4}=\underset{t\to +\infty }{\lim }\frac{50t}{t\left(1+\frac{4}{t}\right)}=\underset{t\to +\infty }{\lim }\frac{50}{1+\frac{4}{t}}$= 50.

Ý nghĩa: Tối đa một nhân viên chỉ có thể lắp được 50 bộ phận mỗi ngày.

a) Tính chi phí trung bình C¯¯¯¯(x) để sản xuất một sản phẩm. 

b) Tính limx→+∞C¯¯¯¯(x) và cho biết ý nghĩa của kết quả. 

Trả lời:

a) C¯¯¯¯(x)=C(x)x=50000+105xx

b) Ta có: limx→+∞C¯¯¯¯(x)=limx→+∞50000+105xx=105

Vậy khi số sản phẩm càng lớn thì chi phí trung bình để sản xuất một sản phẩm tiến dần đến 105 (nghìn đồng).