Giải SGK Toán 11 Cánh Diều Bài 5: Hình lăng trụ và hình hộp

Câu hỏi khởi động: Trong thực tiễn, ta thường gặp nhiều đồ dùng, vật thể gợi nên hình ảnh hình lăng trụ, hình hộp. Chẳng hạn: Khung lịch để bàn (Hình 68); Tháp đôi Puerta de Europa ở Madrid, Tây Ban Nha (Hình 69), …

Hình lăng trụ và hình hộp là hình như thế nào?

Trả lời:

- Hình gồm hai đa giác A1A2…An, A1’A2’…An’ và các bình bình hành A1A2A2’A1’, A2A3A3’A2’, …, AnA1A1’An’ được gọi là hình lăng trụ, kí hiệu là A1A2…An.A1’A2’…An’. Hình hộp là hình lăng trụ có đáy là hình bình hành.

I. Hình lăng trụ

Hoạt động 1: Cho hai mặt phẳng song song (P) và (P’). Trong mặt phẳng (P), cho đa giác A1A2….An. Qua các đỉnh A1,A2,...,An vẽ các đường thẳng song song với nhau và cắt mặt phẳng (P’) lần lượt tại A′1,A2­′,...,A′n (Hình 70 minh hoạ cho trường hợp n = 5).

a) Các tứ giác A1A2A′2A′1,A2A3A′3A′2,…,AnA1A′1A′n là những hình gì?

b) Các cạnh tương ứng của hai đa giác A1A2…An và A′1A′2…A′n có đặc điểm gì?

Trả lời:

a) Ta có: (P) // (P’);

               (A1A2A′2A′1)∩(P)=A1A2;

               (A1A2A′2A′1)∩(P′)=A′1A′2.

Do đó A1A2//A′1A′2.

Trong mp (A1A2A′2A′1), tứ giác A1A2A′2A′1 có A1A′1//A2A′2 và A1A2//A′1A′2

Do đó A1A2A′2A′1 là hình bình hành.

Chứng minh tương tự ta có: các tứ giác A2A3A′3A′2,…,AnA1A′1A′n cũng là những hình bình hành.

Vậy các tứ giác A1A2A′2A′1,A2A3A′3A′2,…,AnA1A′1A′n là những hình bình hành.

b) Theo câu a, A1A2A′2A′1 là hình bình hành nên A1A2=A′1A′2

Tương tự như vậy, ta kết luận các cạnh tương ứng của hai đa giác A1A2…An và A′1A′2…A′n có độ dài bằng nhau.

Hoạt động 2: Từ định nghĩa hình lăng trụ, nhận xét đặc điểm các mặt bên, cạnh bên và hai mặt đáy của hình lăng trụ.

Trả lời:

Từ định nghĩa hình lăng trụ, ta có các nhận xét sau:

• Các cạnh bên của hình lăng trụ song song và bằng nhau.

• Các mặt bên của hình lăng trụ là các hình bình hành.

• Hai mặt đáy của hình lăng trụ là hai đa giác có các cạnh tương ứng song song và bằng nhau.

Luyện tập, vận dụng 1: Cho một số ví dụ về những đồ dùng, vật thể trong thực tế có dạng hình lăng trụ. 

Trả lời:

- Một số ví dụ về những đồ dùng, vật thể trong thực tế có dạng hình lăng trụ: tòa nhà, khối rubik, viên đá viên, ...

II. Hình hộp

Hoạt động 3: Vẽ hình lăng trụ ABCD.A’B’C’D’ có đáy ABCD là hình bình hành.

Trả lời:

Hình lăng trụ ABCD.A’B’C’D’ có đáy ABCD là hình bình hành:

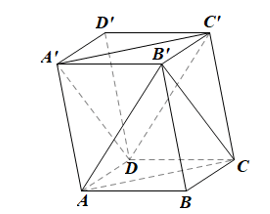
Luyện tập, vận dụng 2: Hãy liệt kê các đường chéo của hình hộp ABCD.A'B'C'D' (Hình 73). 

Trả lời:

- Các đường chéo của hình hộp ABCD.A'B'C'D' là: A'C, AC', D'B, DB'.

Hoạt động 4: Nêu nhận xét gì về hai mặt phẳng chứa hai mặt đối diện của hình hộp.

Trả lời:

Nhận xét: Hai mặt phẳng lần lượt chứa hai mặt đối diện của hình hộp song song với nhau.

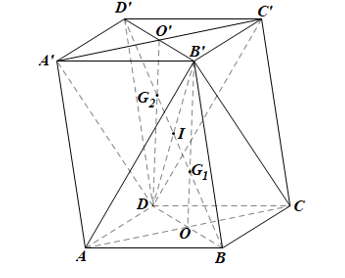
Luyện tập, vận dụng 3: Cho hình hộp ABCD.A'B'C'D'. Chứng minh rằng bốn mặt phẳng (ABC'D'), (BCD'A'), (CDA'B'), (DAB'C') cùng đi qua một điểm. 

Trả lời:

Theo kết quả của ví dụ 3: Các đường chéo của hình hộp cắt nhau tại trung điểm mỗi đường. 

Gọi I là trung điểm của A'C

Ta có: Đường chéo hình hộp ABCD.A'B'C'D' là A'C, AC', D'B, DB'

Mà AC', D'B thuộc (ABC'D'); A'C, D'B thuộc (BCD'A'); A'C, DB' thuộc (CDA'B'); AC', DB' thuộc (DAB'C') 

Do đó: Bốn mặt phẳng cùng đi qua điểm I (I là giao điểm của 4 đường chéo).  

Bài tập

Bài tập 1: Cho hình hộp ABCD.A’B’C D’.

a) Chứng minh rằng (ACB’) // (A’C’D).

b) Gọi G1, G2 lần lượt là giao điểm của BD’ với các mặt phẳng (ACB’) và (A’C’D). Chứng minh rằng G1, G2 lần lượt là trọng tâm của hai tam giác ACB’ và A’C’D.

c) Chứng minh rằng BG1 = G1G2 = D’G2.

Trả lời:

a)

Ta có: (ABCD) // (A’B’C’D’) ( do ABCD.A’B’C’D’ là hình hộp);

           (ABCD) ∩ (ACC’A’) = AC;

           (A’B’C’D’) ∩ (ACC’A’) = A’C’.

Do đó AC // A’C’.

Mà A’C’ ⊂ (A’C’D) nên AC // (A’C’D).

Chứng minh tương tự ta cũng có AB’ // DC’ mà DC’ ⊂ (A’C’D) nên AB’ // (A’C’D).

Ta có: AC // (A’C’D);

          AB’ // (A’C’D);

          AC, AB’ cắt nhau tại điểm A và cùng nằm trong mp(ACB’).

Do đó (ACB’) // (A’C’D).

b)

• Gọi O là tâm hình bình hành đáy ABCD, I là giao điểm của BD’ và DB’.

Tứ giác BDD’B’ có BB’ // DD’ và BB’ = DD’ nên là hình bình hành.

Do đó hai đường chéo BD’ và DB’ cắt nhau tại trung điểm I của mỗi đường.

Trong mp(BDD’B’), BD’ cắt B’O tại G1.

Mà B’O ⊂ (ACB’) nên G1 là giao điểm của BD’ với (ACB’).

Trong mp(BDD’B’), xét $\Delta$BDB’ có hai đường trung tuyến BI, B’O cắt nhau tại G1 nên G1 là trọng tâm của DBDB’

Do đó $\frac{B^{\prime }{G}_1}{BO}=\frac{2}{3}$

Trong (ACB’), xét $\Delta$ACB’ có B’O là đường trung tuyến và $\frac{B^{\prime }{G}_1}{BO}=\frac{2}{3}$

Suy ra G1 là trọng tâm của $\Delta$ACB’.

• Gọi O’ là tâm hình bình hành đáy A’B’C’D’.

Chứng minh tương tự như trên ta cũng có: G2 là trọng tâm của $\Delta$DD’B’ nên $\frac{D{G}_2}{D{O}^{\prime }}=\frac{2}{3}$

Trong (A’C’D), $\Delta$A’C’D có DO’ là đường trung tuyến và  $\frac{D{G}_2}{D{O}^{\prime }}=\frac{2}{3}$

Suy ra G2 là trọng tâm của $\Delta$A’C’D.

c) Theo chứng minh câu b, ta có:

• G1 là trọng tâm của $\Delta$BDB’ nên $\frac{B{G}_1}{BI}=\frac{2}{3}$  và $\frac{I{G}_1}{B{G}_1}=\frac{1}{2}$

• G2 là trọng tâm của  $\Delta$DD’B’ nên $\frac{D^{\prime }{G}_2}{D^{\prime }I}=\frac{2}{3}$  và $\frac{I{G}_2}{D^{\prime }{G}_2}=\frac{1}{2}$

Do đó $\frac{B{G}_1}{BI}=\frac{D^{\prime }{G}_2}{D^{\prime }I}=\frac{2}{3}$  và $\frac{I{G}_1}{B{G}_1}=\frac{I{G}_2}{D^{\prime }{G}_2}=\frac{1}{2}$

Ta có: $\frac{B{G}_1}{BI}=\frac{D^{\prime }{G}_2}{D^{\prime }I}$ và BI = D’I (do I là trung điểm của BD’)

Suy ra BG1 = D’G2.

Lại có $\frac{I{G}_1}{B{G}_1}=\frac{I{G}_2}{D^{\prime }{G}_2}=\frac{1}{2}$  nên IG1 = IG2 = $\frac{1}{2}$ BG1

Do đó G1G2 = IG1 + IG2 = $\frac{1}{2}$ BG1 + $\frac{1}{2}$ BG1 = BG1.

Vậy BG1 = G1G2 = D’G2.

Bài tập 2: Cho hình hộp ABCD.A'B'C'D'. Gọi M, N, P, Q lần lượt là trung điểm của các cạnh BC, AA', C'D', AD'. Chứng minh rằng: 

a) NQ ∥ A'D' và NQ = 12A'D';

b) Tứ giác MNQC là hình bình hành;

c) MN ∥ (ACD');

d) (MNP) ∥ (ACD'). 

Trả lời:

a) Ta có: N là trung điểm của AA' nên ANAA′=12

Q là trung điểm của AD' nên AQAD′=12

Theo định lí Ta-lét ta có: NQ // A'D'

Suy ra: NQA′D′=ANAA′=12 nên NQ=12A′D′

b) Ta có: NQ // A'D' mà A'D' // BC nên NQ // BC hay NQ // MC (1)

Ta có: NQ=12A′D′ mà A'D' = BC, MC = 12 BC nên NQ = MC (2)

(1)(2) suy ra: MNQC là hình bình hành

c) Ta có: MNCQ là hình bình hành nên MN // CQ

Mà CQ thuộc (ACD') 

Nên MN // (ACD')

d) Gọi O là trung điểm của AC

△ACB có: O, M là trung điểm của AC, BC 

Suy ra: OM // AB nên OM = 12 AB 

Mà AB = C'D', D'P = 12 C'D 

Suy ra: OM = D'P (1)

Ta có: OM // AB, AB // C'D' nên OM // C'D' hay OM // D'P (2)

(1)(2) suy ra OMPD' là hình bình hành. Do đó: MP // OD'

Mà OD' thuộc (ACD') 

Suy ra: MP // (ACD') 

Mà MN thuộc (ACD') (câu c) 

Do đó: (MNP) // (ACD'). 

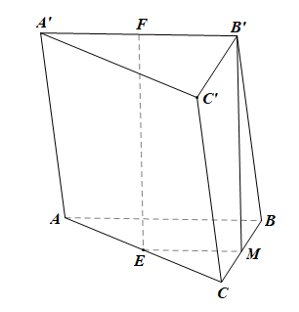
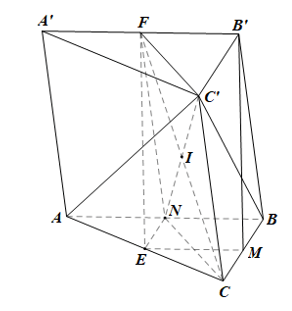
Bài tập 3: Cho hình lăng trụ tam giác ABC.A’B’C’. Gọi E, F lần lượt là trung điểm của các cạnh AC và A’B’.

a) Chứng minh rằng EF // (BCC’B’).

b) Gọi I là giao điểm của đường thẳng CF với mặt phẳng (AC’B). Chứng minh rằng I là trung điểm đoạn thẳng CF.

Trả lời:

a)

Gọi M là trung điểm của BC.

Trong mp(ABC), xét $\Delta$ABC có E, M lần lượt là trung điểm của AC, BC nên EM là đường trung bình của tam giác

Do đó EM // AB và EM = $\frac{1}{2}$ AB.

Mà AB // A’B’ nên EM // A’B’ hay EM // FB’.

Lại có AB = A’B’ và FB’ = $\frac{1}{2}$ A’B’ nên EM = FB’.

Trong mp(EMB’F), xét tứ giác EMB’F có EM // FB’ và EM = FB’ nên là hình bình hành.

Do đó EF // B’M, mà B’M ⊂ (BCC’B’) nên EF // (BCC’B’).

b)

Gọi N là trung điểm của AB.

Trong mp(ABB’A’), xét hình bình hành ABB’A’ cũng là hình thang có N, F lần lượt là trung điểm của AB, A’B’ nên NF là đường trung bình của hình thang

Do đó NF // BB’ và $NF=\frac{A{A}^{\prime }+B{B}^{\prime }}{2}=\frac{2B{B}^{\prime }}{2}=B{B}^{\prime }$ .

Mà BB’ // CC’ nên NF // CC’.

Lại có BB’ = CC’ nên NF = CC’.

Trong mp(NFC’C), xét tứ giác NFC’C có NF // CC’ và NF = CC’ nên là hình bình hành.

Do đó hai đường chéo CF và NC’ cắt nhau tại trung điểm của mỗi đường.

Lại có NC’ ⊂ (ABC’) nên CF cắt (ABC’) tại trung điểm I của CF.

Vậy CF cắt (ABC’) tại trung điểm I của CF.