Giải SGK Toán 11 Cánh Diều Bài 4: Hai mặt phẳng song song

Câu hỏi khởi động: Trong cuộc sống, chúng ta bắt gặp rất nhiều đồ dùng, vật thể gợi nên hình ảnh của các mặt phẳng song song, chẳng hạn như giá để đồ (Hình 58).

Làm thế nào để nhận ra được hai mặt phẳng song song? Hai mặt phẳng song song thì có tính chất gì?  

Trả lời:

- Hai mặt phẳng song song nếu chúng không có điểm chung.

- Nếu một mặt phẳng chứa hai đường thẳng cắt nhau và hai đường thẳng này cùng song song với một mặt phẳng khác thì hai mặt phẳng song song với nhau. 

I. Hai mặt phẳng song song

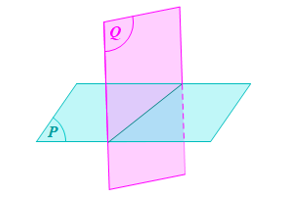
Hoạt động 1: Trong không gian cho hai mặt phẳng phân biệt (P) và (Q).

Nếu (P) và (Q) có một điểm chung thì chúng có bao nhiêu điểm chung? Các điểm chung đó có tính chất gì?

Trả lời:

Nếu (P) và (Q) có một điểm chung thì chúng có vô số điểm chung. Các điểm chung đó cùng nằm trên một đường thẳng.

Luyện tập, vận dụng 1: Nêu ví dụ trong thực tiễn minh họa hình ảnh hai mặt phẳng song song. 

Trả lời:

- Trong thực tiễn có nhiều hình ảnh về hai mặt phẳng song song. Chẳng hạn: các mặt của giá để đồ; trần nhà và mặt sàn của một căn phòng; hai bức tường đối diện nhau; ...

II. Điều kiện và tính chất

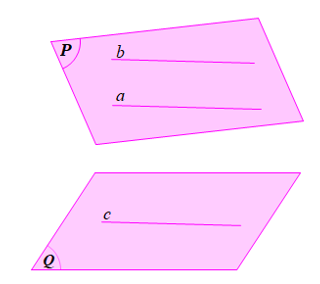
Hoạt động 2: Cho hai mặt phẳng phân biệt (P) và (Q). Mặt phẳng (P) chứa hai đường thẳng a, b cắt nhau và a, b cùng song song với mặt phẳng (Q) (Hình 61). Hai mặt phẳng (P) và (Q) có điểm chung hay không?

Trả lời:

Nếu hai mặt phẳng (P) và (Q) có một điểm chung thì chúng có đường thẳng chung d.

Ta có:  a // (Q);

            a ⊂ (P);

           (P) ∩ (Q) = d.

Suy ra a // d.

Tương tự ta cũng có b // d.

Mà a, b, d cùng nằm trong mặt phẳng (P) nên a // b // d, điều này mâu thuẫn với giả thiết a, b cắt nhau trong (P).

Vậy hai mặt phẳng (P) và (Q) không có điểm chung hay (P) // (Q).

Hoạt động 3: Cho mặt phẳng (Q) và điểm M nằm ngoài mặt phẳng (Q).

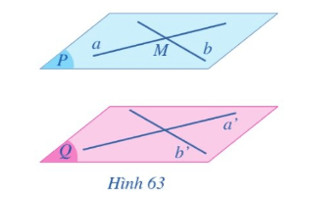
a) Trong mặt phẳng (Q) vẽ hai đường thẳng a’, b’ cắt nhau. Qua điểm M kẻ các đường thẳng a và b lần lượt song song với a’, b’. Gọi (P) là mặt phẳng xác định bởi hai đường thẳng (cắt nhau) a và b (Hình 63). Mặt phẳng (P) có song song với mặt phẳng (Q) hay không?

b) Xét mặt phẳng (R) đi qua điểm M và song song với mặt phẳng (Q). Hai mặt phẳng (R) và (P) có trùng nhau hay không?

Trả lời:

a) Ta có: a // a’ mà a’ ⊂ (Q) nên a // (Q);

               b // b’ mà b’ ⊂ (Q) nên b // (Q).

Do a // (Q);

      b // (Q);

      a, b cắt nhau tại M và cùng nằm trong mặt phẳng (P)

Suy ra (P) // (Q).

b) Do (R) // (Q) nên trong mp(R) tồn tại hai đường thẳng a’’, b’’ đi qua M và lần lượt song song với a’, b’ trong mp(Q).

Ta có: a // a’, a’’ // a’ nên a // a’’.

Mà a’’ ∈ (R), do đó a // (R)

Do hai mặt phẳng (P) và (R) có một điểm chung nên chúng có đường thẳng chung d.

Ta có:  a // (R);

            a ⊂ (P);

           (P) ∩ (R) = d.

Suy ra a // d.

Mà a, d cùng nằm trong mặt phẳng (P) và cùng đi qua điểm M nên đường thẳng a chính là giao tuyến của hai mặt phẳng (P) và (R).

Chứng minh tương tự ta cũng có đường thằng b cũng là giao tuyến của hai mặt phẳng (P) và (R).

Như vậy, hai mặt phẳng (P) và (R) có hai giao tuyến a và b nên (P) và (R) là hai mặt phẳng trùng nhau.

Luyện tập, vận dụng 2: Cho tứ diện ABCD. Các điểm M, N, P, I, J, K lần lượt là trung điểm của BC, CD, DB, AM, AN, AP. Chứng minh rằng (IJK) ∥ (BCD). 

Trả lời:

△AMP có: I, K là trung điểm AM, AP

Suy ra: IK // MP mà MP thuộc (BCD) nên IK // (BCD) (1)

△ANP có: J, K là trung điểm AN, AP

Suy ra: JK // NP mà NP thuộc (BCD) nên JK // (BCD) (2)

(1)(2) suy ra: (IJK) // (BCD). 

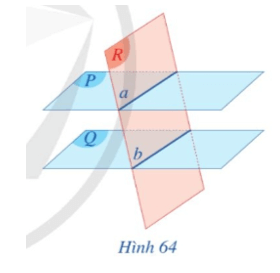
Hoạt động 4: Cho hai mặt phẳng song song (P) và (Q). Mặt phẳng (R) cắt mặt phẳng (P) theo giao tuyến a.

a) Mặt phẳng (R) có cắt mặt phẳng (Q) hay không? Tại sao?

b) Trong trường hợp mặt phẳng (R) cắt mặt phẳng (Q) theo giao tuyến b, hãy nêu nhận xét về vị trí tương đối giữa hai giao tuyến a và b (Hình 64).

Trả lời:

a) Do (P) // (Q) và (R) ∩ (P) = a nên (R) // (Q) hoặc (R) cắt (Q).

Giả sử (R) // (Q).

Khi đó qua đường thẳng a có hai mặt phẳng song song với (Q) là mặt phẳng (P) và (R) nên hai mặt phẳng này trùng nhau, điều này mâu thuẫn với giả thiết (R) cắt (P).

Vậy (R) cắt Q.

b) Ta có: a ⊂ (P); b ⊂ (Q) mà (P) // (Q) nên a và b không có điểm chung.

Lại có hai đường thẳng a và b cùng nằm trên mp(R)

Do đó a // b.

Luyện tập, vận dụng 3: Cho hai mặt phẳng (P) và (Q) song song với nhau. Đường thẳng a cắt hai mặt phẳng trên theo thứ tự A, B. Đường thẳng b song song với đường thẳng a và cắt hai mặt phẳng (P) và (Q) lần lượt tại A', B'. Chứng minh rằng AB = A'B'. 

Trả lời:

Ta có (P) // (Q) mà AA' thuộc (P), BB' thuộc (Q) nên AA' // BB' (1) 

Ta có a // b mà AB thuộc a, A'B' thuộc b nên AB // A'B' (2)

(1)(2) suy ra: AA'B'B là hình bình hành. Do đó AB = A'B'. 

III. Định lí Thales

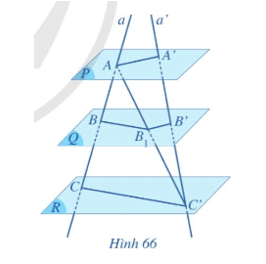
Hoạt động 5: Cho ba mặt phẳng song song (P), (Q), (R). Hai cát tuyến bất kì a và a’ cắt ba mặt phẳng song song lần lượt tại các điểm A, B, C và A’, B’, C’. Gọi B1 là giao điểm của AC’ với mặt phẳng (Q) (Hình 66).

a) Nêu vị trí tương đối của BB1 và CC’; B1B’ và AA’.

b) Có nhận xét gì về các tỉ số: $\frac{AB}{A{B}_1},\frac{BC}{B_1{C}^{\prime }}$  và $\frac{CA}{C^{\prime }A};$$\frac{A{B}_1}{A^{\prime }{B}^{\prime }},\frac{B_1{C}^{\prime }}{B^{\prime }{C}^{\prime }}$  và $\frac{C^{\prime }A}{C^{\prime }{A}^{\prime }}$ .

c) Từ kết quả câu a) và câu b), so sánh các tỉ số $\frac{AB}{A^{\prime }{B}^{\prime }},\frac{BC}{B^{\prime }{C}^{\prime }}$  và $\frac{CA}{C^{\prime }{A}^{\prime }}$ .

Trả lời:

a) Ta có: B ∈ (ACC’) và B ∈ (Q) nên B là giao điểm của (ACC’) và (Q);

               B­1 ∈ (ACC’) và B1 ∈ (Q) nên B1 là giao điểm của (ACC’) và (Q).

Do đó (ACC’) ∩ (Q) = BB1.

Tương tự, ta có (ACC’) ∩ (R) = CC’.

Ta có: (Q) // (R);

           (ACC’) ∩ (Q) = BB1;

           (ACC’) ∩ (R) = CC’.

Suy ra BB1 // CC’.

Chứng minh tương tự ta cũng có: (P) // (Q);

                                                      (AA’C’) ∩ (P) = AA’;

                                                      (AA’C’) ∩ (Q) = B1B’.

Suy ra B1B’ // AA’.

b) Trong mp(ACC’), xét DACC’ có: BB1 // CC’ nên theo định lí Thalès ta có:

• $\frac{AB}{AC}=\frac{A{B}_1}{A{C}^{\prime }}$ , suy ra $\frac{AB}{A{B}_1}=\frac{CA}{C^{\prime }A}$ ;

• $\frac{BC}{AC}=\frac{B_1{C}^{\prime }}{A{C}^{\prime }}$ , suy ra $\frac{BC}{B_1{C}^{\prime }}=\frac{CA}{C^{\prime }A}$ .

Do đó $\frac{AB}{A{B}_1}=\frac{BC}{B_1{C}^{\prime }}=\frac{CA}{C^{\prime }A}$ .

Trong mặt phẳng (AA’C’), xét $\Delta$AA’C’có: B1B’ // AA’ nên theo định lí Thalès ta có:

• $\frac{A{B}_1}{A{C}^{\prime }}=\frac{A^{\prime }{B}^{\prime }}{A^{\prime }{C}^{\prime }}$ , suy ra $\frac{A{B}_1}{A^{\prime }{B}^{\prime }}=\frac{C^{\prime }A}{C^{\prime }{A}^{\prime }}$ ;

• $\frac{B_1{C}^{\prime }}{A{C}^{\prime }}=\frac{B^{\prime }{C}^{\prime }}{A^{\prime }{C}^{\prime }}$ , suy ra $\frac{B_1{C}^{\prime }}{B^{\prime }{C}^{\prime }}=\frac{C^{\prime }A}{C^{\prime }{A}^{\prime }}$ .

Do đó $\frac{A{B}_1}{A^{\prime }{B}^{\prime }}=\frac{B_1{C}^{\prime }}{B^{\prime }{C}^{\prime }}=\frac{C^{\prime }A}{C^{\prime }{A}^{\prime }}$ .

c) Theo chứng minh ở câu b ta có:

•  $\frac{AB}{AC}=\frac{A{B}_1}{A{C}^{\prime }}$và $\frac{A{B}_1}{A{C}^{\prime }}=\frac{A^{\prime }{B}^{\prime }}{A^{\prime }{C}^{\prime }}$  nên $\frac{AB}{AC}=\frac{A^{\prime }{B}^{\prime }}{A^{\prime }{C}^{\prime }}\left(=\frac{A{B}_1}{A{C}^{\prime }}\right)$

Do đó $\frac{AB}{A^{\prime }{B}^{\prime }}=\frac{CA}{C^{\prime }{A}^{\prime }}$.

• $\frac{BC}{AC}=\frac{B_1{C}^{\prime }}{A{C}^{\prime }}$  và $\frac{B_1{C}^{\prime }}{A{C}^{\prime }}=\frac{B^{\prime }{C}^{\prime }}{A^{\prime }{C}^{\prime }}$ nên $\frac{BC}{AC}=\frac{B^{\prime }{C}^{\prime }}{A^{\prime }{C}^{\prime }}\left(=\frac{B_1{C}^{\prime }}{A{C}^{\prime }}\right)$

Do đó $\frac{BC}{B^{\prime }{C}^{\prime }}=\frac{CA}{C^{\prime }{A}^{\prime }}$ .

Vậy $\frac{AB}{A^{\prime }{B}^{\prime }}=\frac{BC}{B^{\prime }{C}^{\prime }}=\frac{CA}{C^{\prime }{A}^{\prime }}$ .

Luyện tập, vận dụng 4: Bạn Minh cho rằng: Nếu a, b là hai cát tuyến bất kì cắt ba mặt phẳng song song (P), (Q), (R) lần lượt tại các điểm A, B, C và A', B', C' thì ABBC=A′B′B′C′=ACA′C′. 

Phát biểu của bạn Minh có đúng không? Vì sao? 

Trả lời:

Ý kiến sai. Vì: CAC′A′=AB+BCA′B′+B′C′≠ABBC≠A′B′B′C′

Bài tập

Bài tập 1: Bạn Chung cho rằng: Nếu mặt phẳng (P) chứa hai đường thẳng a, b và a, b cùng song song với mặt phẳng (Q) thì (P) luôn song song với (Q). Phát biểu của bạn Chung có đúng không? Vì sao?

Trả lời:

Phát biểu của bạn Chung không đúng vì trong trường hợp này, để (P) // (Q) thì hai đường thẳng a và b trong mặt phẳng (P) cần thêm điều kiện cắt nhau tại một điểm.

Chẳng hạn: xét trường hợp hai đường thẳng a và b song song với nhau trong mp(P) (hình vẽ).

Do a // (Q) nên tồn tại đường thẳng c nằm trên (Q) sao cho c // a.

Do a // b và c // a nên a // b // c.

Ta có: b // c mà c ⊂ (Q) nên b // (Q).

Trong hình vẽ trên, tuy a // (Q) và b // (Q) nhưng (P) không song song với (Q).

Bài tập 2: Trong mặt phẳng (P) cho hình bình hành ABCD. Qua A, B, C, D lần lượt vẽ bốn đường thẳng a, b, c, d đôi một song song với nhau và không nằm trong mặt phẳng (P). Một mặt phẳng cắt a, b, c, d lần lượt tại bốn điểm A', B', C', D'. Chứng minh rằng A'B'C'D' là hình bình hành. 

Trả lời:

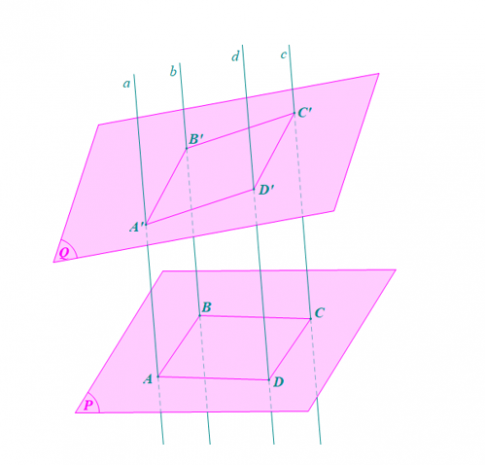
Ta có: AB // CD (do ABCD là hình bình hành).

Mà CD ⊂ mp(CDD’C’) nên AB // (CDD’C’).

Lại có a // d nên A’A // D’D

Mà D’D ⊂ mp(CDD’C’) nên A’A // (CDD’C’).

Ta có: AB // (CDD’C’);

           A’A // (CDD’C’);

           AB, A’A cắt nhau tại A và cùng nằm trong (ABB’A’)

Do đó (ABB’A’) // (CDD’C’).

Ta có: (ABB’A’) // (CDD’C’);

           (ABB’A’) ∩ (Q) = A’B’;

           (CDD’C’) ∩ (Q) = C’D’.

Do đó A’B’ // C’D’.

• Tương tự, (ADD’A’) // (BCC’B);

                 (ADD’A’) ∩ (Q) = A’D’;

                 (BCC’B) ∩ (Q) = B’C’.

Do đó A’D’ // B’C’.

Tứ giác A’B’C’D’ có A’B’ // C’D’ và A’D’ // B’C’ nên A’B’C’D là hình bình hành.

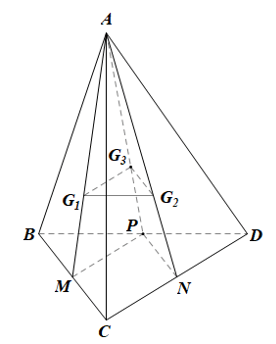
Bài tập 3: Cho tứ diện ABCD. Lấy G1, G2, G3 lần lượt là trọng tâm của các tam giác ABC, ACD, ADB.

a) Chứng minh rằng (G1G2G3) // (BCD).

b) Xác định giao tuyến của mặt phẳng (G1G2G3) với mặt phẳng (ABD).

Trả lời:

a)

Gọi M, N, P lần lượt là trung điểm của BC, CD, DB.

Trong mp(ABC), xét $\Delta$ABC có G1 là trọng tâm của tam giác nên $\frac{A{G}_1}{AM}=\frac{2}{3}$ ;

Trong mp(ACD), xét $\Delta$ACD có G2 là trọng tâm của tam giác nên $\frac{A{G}_2}{AN}=\frac{2}{3}$ ;

Trong mp(ABD), xét $\Delta$ABD có G3 là trọng tâm của tam giác nên $\frac{A{G}_3}{AP}=\frac{2}{3}$ .

Trong mp(AMP), xét $\Delta$AMP có $\frac{A{G}_1}{AM}=\frac{A{G}_3}{AP}=\frac{2}{3}$  nên G1G3­ // MP (theo định lí Thalès đảo).

Mà MP ⊂ (BCD) nên G1G3­ // (BCD).

Chứng minh tương tự ta cũng có $\frac{A{G}_2}{AN}=\frac{A{G}_3}{AP}=\frac{2}{3}$  nên G2G3 // NP (theo định lí Thalès đảo).

Mà NP ⊂ (BCD) nên G2G3­ // (BCD).

Ta có: G1G3­ // (BCD);

           G2G3­ // (BCD);

           G1G3, G2G3 cắt nhau tại G3 và cùng nằm trong mp(G1G2G3).

Do đó (G1G2G3) // (BCD).

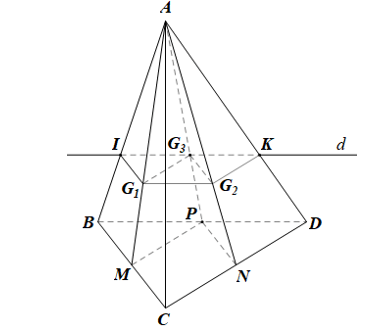
b)

Ta có: B, D cùng thuộc hai mặt phẳng (ABD) và (BCD) nên (ABD) ∩ (BCD) = BD.

Giả sử (ABD) ∩ (G1G2G3) = d.

Ta có: (G1G2G3) // (BCD);

           (ABD) ∩ (BCD) = BD;

           (ABD) ∩ (G1G2G3) = d.

Suy ra d // BD.

Mà G3 ∈ (ABD) và G3 ∈ (G1G2G3) nên G3­ là giao điểm của (G1G2G3) và (ABD).

Do đó giao tuyến d của hai mặt phẳng (G1G2G3) và (ABD) đi qua điểm G3 và song song với BD, cắt AB, AD lần lượt tại I và K.

Vậy (G1G2G3) ∩ (ABD) = IK.

Bài tập 4: Cho hai hình bình hành ABCD và ABEF không cùng nằm trong một mặt phẳng. 

a) Chứng minh rằng (AFD) ∥ (BEC). 

b) Gọi M là trọng tâm của tam giác ABE. Gọi (P) là mặt phẳng đi qua M và song song với mặt phẳng (AFD). Lấy N là giao điểm của (P) và AC. Tính ANNC. 

Trả lời:

a) Ta có: AD // BC (ABCD là hình bình hành) 

Mà AD thuộc (AFĐ), BC thuộc (BEC) 

Nên (AFD) // (BEC) 

b) Trong (ABEF) kẻ đường thẳng d qua M // AF

Ta có: d cắt AB tại I, d cắt EF tại J (1)

Trong (ABCD) có I thuộc (P) mà (P) // (AFD) 

Suy ra từ I kẻ IH // AD (2) 

(1)(2) suy ra (IJH) trùng (P) và // (AFD) 

Ta có: (P) cắt AC tại N mà AC thuộc (ABCD), IH thuộc (P) và (ABCD) 

Suy ra: IH cắt AC tại N

Ta có các hình bình hành IBCH, IBEJ

Gọi O là trung điểm của AB

Có M là trọng tâm △ABE

Suy ra: MOME=12

Ta có: AB // CD suy ra: AI // CH

Định lí Ta-lét: ANNC=AICH

mà CH = IB (IBCH là hình bình hành)

Suy ra: ANNC=AIIB

Ta có: AB // EF nên OI // EJ

Do đó: OIEJ=MOME=12

Mà EJ = IB (IBEJ là hình bình hành)

Suy ra: OIIB=12 hay IB = 2OI

Ta có: ANNC=AIIB=AO+OI2OI

Mà OA = OB (O là trung điểm AB)

Nên ANNC=OB+OI2OI=2

Do đó: ANNC=2.