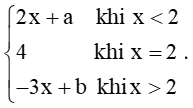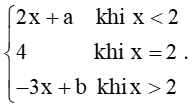Giải SGK Toán 11 Cánh Diều Bài tập cuối chương III

Bài tập 1: Cho hàm số y = f(x) xác định trên khoảng (a; b) và x0 ∈ (a; b). Điều kiện cần và đủ để hàm số y = f(x) liên tục tại x0 là:

A. $\underset{x\to x_0^{+}}{\lim }f\left(x\right)=f\left(x_0\right)$;

B. $\underset{x\to x_0^{-}}{\lim }f\left(x\right)=f\left(x_0\right)$;

C. $\underset{x\to x_0^{+}}{\lim }f\left(x\right)=\underset{x\to x_0^{-}}{\lim }f\left(x\right)$;

D. $\underset{x\to x_0^{+}}{\lim }f\left(x\right)=\underset{x\to x_0^{-}}{\lim }f\left(x\right)=f\left(x_0\right)$.

Đáp án: D

Bài tập 2: Tính các giới hạn sau:

a) lim$\frac{2n^2+6n+1}{8n^2+5}$;

b) lim$\frac{4n^2-3n+1}{3n^3+6n^2-2}$;

c) lim$\frac{\sqrt{4n^2-n+3}}{8n-5}$;

d) lim$\left(4-\frac{2^{n+1}}{3^n}\right)$;

e) lim$\frac{{4.5}^n+2^{n+2}}{{6.5}^n}$;

g) lim$\frac{2+\frac{4}{n^3}}{6^n}$.

Trả lời:

a) lim2n2+6n+18n2+5=lim2+6n+1n28+5n2=14;

b) lim4n2−3n+1−3n3+6n2−2=limn2(4−3n+1n2)n3(−3+6n−2n3)=lim1n.(−43)=0;

c) lim4n2−n+3√8n−5=lim4−1n+3n2√8−5n=14;

d) lim(4−2n+13n)=lim(4−(23)n.2)=4;

e) lim4.5n+2n+26.5n=lim(23+23.(25)n)=23;

g) lim2+4n36n=2+0+∞=0. 

Bài tập 3: Tính các giới hạn sau:

a) $\underset{x\to -3}{\lim }\left(4x^2-5x+6\right)$;

b) $\underset{x\to 2}{\lim }\frac{2x^2-5x+2}{x-2}$;

c) $\underset{x\to 4}{\lim }\frac{\sqrt{x}-2}{x^2-16}$.

Trả lời:

a) $\underset{x\to -3}{\lim }\left(4x^2-5x+6\right)=4{\left(-3\right)}^2$-5.(-3)+6 = -3.

b) $\underset{x\to 2}{\lim }\frac{2x^2-5x+2}{x-2}=\underset{x\to 2}{\lim }\frac{\left(x-2\right)\left(2x-1\right)}{x-2}=\underset{x\to 2}{\lim }\left(2x-1\right)=3$.

c) $\underset{x\to 4}{\lim }\frac{\sqrt{x}-2}{x^2-16}=\underset{x\to 4}{\lim }\frac{\sqrt{x}-2}{\left(x-4\right)\left(x+4\right)}=\underset{x\to 4}{\lim }\frac{\sqrt{x}-2}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)\left(x+4\right)}$

$=\underset{x\to 4}{\lim }\frac{1}{\left(\sqrt{x}+2\right)\left(x+4\right)}=\frac{1}{32}$

Bài tập 4: Tính các giới hạn sau:

a) $\underset{x\to -\infty }{\lim }\frac{6x+8}{5x-2}$;

b) $\underset{x\to +\infty }{\lim }\frac{6x+8}{5x-2}$;

c) $\underset{x\to -\infty }{\lim }\frac{\sqrt{9x^2-x+1}}{3x-2}$;

d) $\underset{x\to +\infty }{\lim }\frac{\sqrt{9x^2-x+1}}{3x-2}$;

e) $\underset{x\to -2^{-}}{\lim }\frac{3x^2+4}{2x+4}$;

g) $\underset{x\to -2^{+}}{\lim }\frac{3x^2+4}{2x+4}$.

Trả lời:

a) limx→−∞6x+85x−2=65;

b) limx→+∞6x+85x−2=65;

c) limx→−∞9x2−x+1√3x−2=1;

d) limx→+∞9x2−x+1√3x−2=1;

e) limx→−2−3x2+42x+4=−∞;

g) limx→−2+3x2+42x+4=+∞. 

Bài tập 5: Cho hàm số f(x) = 

a) Với a = 0, b = 1, xét tính liên tục của hàm số tại x = 2.

b) Với giá trị nào của a, b thì hàm số liên tục tại x = 2?

c) Với giá trị nào của a, b thì hàm số liên tục trên tập xác định?

Trả lời:

a) Với a = 0, b = 1, hàm số f(x) = 

Với x < 2 thì f(x) = 2x là hàm liên tục.

Với x > 2 thì f(x) = – 3x + 1 là hàm liên tục.

Tại x = 2 ta có:

$\underset{x\to 2^{-}}{\lim }f\left(x\right)=\underset{x\to 2^{-}}{\lim }2x=4$, $\underset{x\to 2^{+}}{\lim }f\left(x\right)=\underset{x\to 2^{+}}{\lim }\left(-3x+1\right)=-5$.

Suy ra $\underset{x\to 2^{-}}{\lim }f\left(x\right)\ne \underset{x\to 2^{+}}{\lim }f\left(x\right)$. Do đó không tồn tại $\underset{x\to 2}{\lim }f\left(x\right)$.

Vậy hàm số tiên tục trên ( – ∞; 2) và (2; +∞).

b) Ta có:

$\underset{x\to 2^{-}}{\lim }f\left(x\right)=\underset{x\to 2^{-}}{\lim }\left(2x+a\right)=4+a$, $\underset{x\to 2^{+}}{\lim }f\left(x\right)=\underset{x\to 2^{+}}{\lim }\left(-3x+b\right)=-6+b$

Để hàm số liên tục tại x = 2 thì:

$\underset{x\to 2^{-}}{\lim }f\left(x\right)=\underset{x\to 2^{+}}{\lim }f\left(x\right)=f\left(2\right)$.

Vậy với a = 0 và b = 10 thì hàm số liên tục tại x = 2.

c) Tập xác định của hàm số là: ℝ.

Để hàm số liên tục trên ℝ thì hàm số liên tục tại x = 2. Vì vậy với a = 0 và b = 10 thỏa mãn điều kiện.

Bài tập 6: Từ độ cao 55,8 m của tháp nghiêng Pisa nước Ý, người ta thả một quả bóng cao su chạm xuống đất (Hình 18). Giả sử mỗi lần chạm đất quả bóng lại này lên độ cao bằng $\frac{1}{10}$độ cao mà quả bóng đạt được trước đó. Gọi Sn là tổng quãng đường di chuyển của quả bóng tính từ lúc thả vật bạn đầu cho đến khi quả bóng đó chạm đất n lần. Tính limSn.

Trả lời:

Gọi (un) là dãy số thể hiện quãng đường di chuyển của quả bóng sau mỗi lần chạm đất.

Ta có: u1 = 55,8, u2 = $\frac{1}{10}$.u1; u3 = ${\left(\frac{1}{10}\right)}^2$.u1; ...; un = ${\left(\frac{1}{10}\right)}^{n-1}$.u1.

Khi đó dãy (un) lập thành một cấp số nhân lùi vô hạn có số hạng đầu u1 = 55,8 và công bội q=$\frac{1}{10}$thỏa mãn |q| < 1.

Suy ra $S_n=u_1+u_2+\mathrm{...}+u_n+\mathrm{...}=\frac{55,8}{1-\frac{1}{10}}=62$(m).

Vậy tổng độ dài quãng đường di chuyển của quả bóng tính từ lúc thả ban đầu cho đến khi quả bóng đó chạm đất n lần là 62 m.

Bài tập 7: Cho một tam giác đều ABC cạnh a. Tam giác A1B1C1 có các đỉnh là trung điểm các cạnh của tam giác ABC, tam giác A2B2C2 có các đỉnh là trung điểm các cạnh của tam giác A1B1C1, ..., tam giác An+1Bn+1Cn+1 có các đỉnh là trung điểm các cạnh của tam giác AnBnCn, ... Gọi p1,p2, ..., pn, ... và S1,S2, ..., Sn, ... theo thứ tự là chu vi và diện tích của các tam giác A1B1C1,A2B2C2, ..., AnBnCn, ... . 

a) Tìm giới hạn của các dãy số (pn) và (Sn). 

b) Tìm các tổng p1+p2+...+pn+... và S1+S2+...+Sn+... .

Trả lời:

a) Ta có: p1=a2+a2+a2=3a2, p2=3a4, pn=3a2n

Suy ra: limpn=lim3a.12n=0

Có: SABC=a23√4, SA1B1C1=S4, Sn=a23√4.(14)n

Suy ra: limSn=lima23√4.(14)n=0

b) (pn) là cấp số nhân lùi vô hạn với công bội q=12, ta có: 

p1+p2+...+pn+...=p11−12=2p1=3a

(S_{n}) là cấp số nhân lùi vô hạn với công bội q=14

S1+S2+...+Sn+...=S11−14=43S1=S3=a23√12

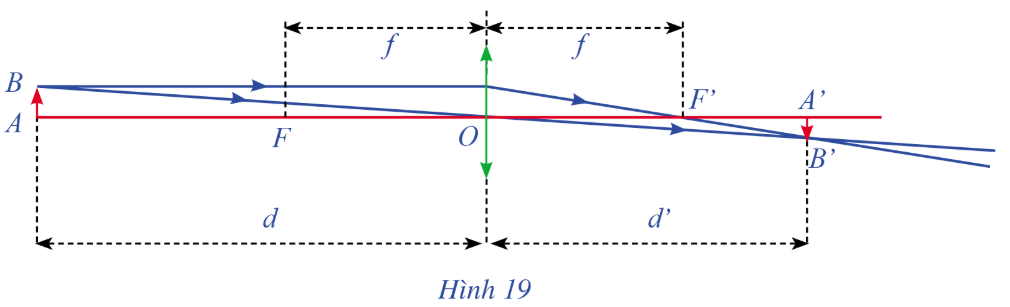
Bài tập 8: Một thấu kính hội tụ có tiêu cự là f. Gọi d và d’ lần lượt là khoảng cách từ một vật thật AB và từ ảnh A’B’ của nó tới quang tâm O của thấu kính như Hình 19. Công thức thấu kính $\frac{1}{d}+\frac{1}{d\text{'}}=\frac{1}{f}$.

a) Tìm biểu thức xác định hàm số d’ = φ(d).

b) Tìm $\underset{d\to f^{+}}{\lim }\phi \left(d\right),\underset{d\to f^{-}}{\lim }\phi \left(d\right)$và $\underset{d\to f}{\lim }\phi \left(d\right)$. Giải thích ý nghĩa của các kết quả tìm được.

Trả lời:

a) Ta có: $\frac{1}{d\text{'}}=\frac{1}{f}-\frac{1}{d}\iff \frac{1}{d\text{'}}=\frac{d-f}{df}\iff d\text{'}=\frac{df}{d-f}$.

b) Ta có:

$\underset{d\to f^{+}}{\lim }\phi \left(d\right)=\underset{d\to f^{+}}{\lim }\frac{df}{d-f}=+\infty ;\underset{d\to f^{-}}{\lim }\phi \left(d\right)=\underset{d\to f^{-}}{\lim }\frac{df}{d-f}=-\infty$;

$\underset{d\to f}{\lim }\phi \left(d\right)=\underset{d\to f}{\lim }\frac{df}{d-f}=\infty$.

Giải thích ý nghĩa: Khi khoảng cách của vật tới thấu kính mà gần với tiêu cự thì khoảng cách ảnh của vật đến thấu kính ra xa vô tận nên lúc đó bằng mắt thường mình không nhìn thấy.