Giải SGK Toán 10 Cánh Diều Bài 1: Mệnh đề toán học - Giải SGK Toán 10 - Cánh Diều

Khởi động: Bạn H’Maryam phát biểu: “Số 15 chia hết cho 5.”, bạn Phương phát biểu: “Việt Nam là một nước ở khu vực Đông Nam Á.”.

Trong hai phát biểu trên, phát biểu nào là mệnh đề toán học?

Trả lời:

- Mệnh đề "Số 15 chia hết cho 5" là một mệnh đề toán học.

1. Mệnh đề toán học

Hoạt động 1:

a) Phát biểu của bạn H’Maryam có phải là một câu khẳng định về tính chất chia hết trong toán học hay không?

b) Phát biểu của bạn Phương có phải là một câu khẳng định về một sự kiện trong toán học hay không?

Trả lời:

a) Phát biểu của bạn H’Maryam là một mệnh đề khẳng định về một sự kiện trong toán học nói về tính chất chia hết. Ta gọi đây là mệnh đề toán học.

b) Phát biểu của bạn Phương không phải là một câu khẳng định về một sự kiện trong toán học.

Luyện tập, vận dụng 1: Nêu hai ví dụ về mệnh đề toán học.

Trả lời:

- Ví dụ 1: Tổng các góc của một tứ giác bằng 360^o

- Ví dụ 2: Nếu một thừa số của tích chia hết cho một số thì tích chia hết cho số đó.

Hoạt động 2: Trong hai mệnh đề toán học sau đây, mệnh đề nào là một khẳng định đúng? Mệnh đề nào là một khẳng định sai?

P: “Tổng hai góc đối của một tứ giác nội tiếp bằng 180°”;

Q: “ $\sqrt{2}$ là số hữu tỉ”.

Trả lời:

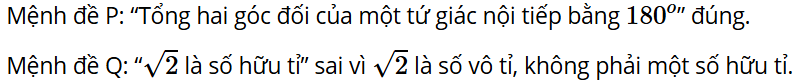
Luyện tập, vận dụng 2: Nêu ví dụ về một mệnh đề đúng và một mệnh đề sai.

Trả lời:

+ Ví dụ về mệnh đề đúng:

- “Số 9 là hợp số”;

- “Tam giác đều có 3 cạnh bằng nhau”;

- “Số 10 chia hết cho cả 2 và 5”;

…

+ Ví dụ về mệnh đề sai:

- “Số nguyên tố nhỏ nhất là 3”, (mệnh đề này sai vì số nguyên tố nhỏ nhất là 2);

- “Số 10 chia hết cho cả 2, 3 và 5”, (sai vì 10 không chia hết cho 3);

- “Hình chữ nhật có 4 góc không bằng nhau”, (sai vì hình chữ nhật có 4 góc vuông, bằng nhau);

2. Mệnh đề chứa biến

Hoạt động 3: Xét câu “n chia hết cho 3” với n là số tự nhiên.

a) Ta có thể khẳng định được tính đúng sai của câu trên hay không?

b) Với n = 21 thì câu “21 chia hết cho 3” có phải là mệnh đề toán học hay không? Nếu là mệnh đề toán học thì mệnh đề đó đúng hay sai?

c) Với n = 10 thì câu “10 chia hết cho 3” có phải là mệnh đề toán học hay không? Nếu là mệnh đề toán học thì mệnh đề đó đúng hay sai?

Trả lời:

a) Ta chưa thể khẳng định được tính đúng sai của câu “n chia hết cho 3” do chưa có giá trị cụ thể của n.

b) Với n = 21 thì câu ”21 chia hết cho 3” là mệnh đề toán học. Mệnh đề này đúng.

c) Với n = 10 thì câu ”10 chia hết cho 3” là mệnh đề toán học. Mệnh đề này sai.

Luyện tập, vận dụng 3: Nêu ví dụ về mệnh đề chứa biến.

Trả lời:

- Ví dụ mệnh đề chứa biến: P(n): "2n là một số không âm".

3. Phủ định của một mệnh đề

Hoạt động 4: Hai bạn Kiên và Cường đang tranh luận với nhau.

Kiên nói: “Số 23 là số nguyên tố”.

Cường nói: “Số 23 không là số nguyên tố”.

Em có nhận xét gì về hai câu phát biểu của Kiên và Cường?

Trả lời:

Hai câu phát biểu của Kiên và Cường đều là các mệnh đề toán học và hai câu này có ý nghĩa trái ngược nhau.

Số 23 là số tự nhiên lớn hơn 1, chỉ có 2 ước là 1 và 23 nên đây là số nguyên tố, do đó phát biểu của Kiên là mệnh đề đúng và phát biểu của Cường là mệnh đề sai.

Luyện tập, vận dụng 4: Lập mệnh đề phủ định của mỗi mệnh đề sau và nhận xét tính đúng sai của mệnh đề phủ định đó.

P: “5,15 là một số hữu tỉ”;

Q: “ 2 023 là số chẵn”.

Trả lời:

4. Mệnh đề kéo theo

Hoạt động 5: Cho n là số tự nhiên. Xét hai mệnh đề:

P: “Số tự nhiên n chia hết cho 6”; Q: “Số tự nhiên n chia hết cho 3”.

Xét mệnh đề R: “Nếu số tự nhiên n chia hết cho 6 thì số tự nhiên n chia hết cho 3”.

Mệnh đề R có dạng phát biểu như thế nào?

Trả lời:

Mệnh đề R: “Nếu số tự nhiên n chia hết cho 6 thì số tự nhiên n chia hết cho 3”.

Ta thấy mệnh đề R có dạng: “Nếu P thì Q”.

Luyện tập, vận dụng 5: Hãy phát biểu một định lí toán học ở dạng mệnh đề kéo theo P ⇒ Q.

Trả lời:

P: "Ba điểm A, B, C cùng thuộc một đường thẳng";

Q: "Ba điểm A, B, C thẳng hàng".

P ⇒ Q: "Nếu ba điểm A, B, C cùng thuộc một đường thẳng thì ba điểm A, B, C thẳng hàng".

5. Mệnh đề đảo. Hai mệnh đề tương đương

Hoạt động 6: Cho tam giác ABC. Xét mệnh đề dạng P ⇒ Q như sau:

“Nếu tam giác ABC vuông tại A thì tam giác ABC có AB2 + AC2 = BC2”.

Phát biểu mệnh đề Q ⇒ P và xác định tính đúng sai của hai mệnh đề P ⇒ Q và Q ⇒ P.

Trả lời:

Luyện tập, vận dụng 6: Cho tam giác ABC. Từ các mệnh đề:

P: “Tam giác ABC đều”, Q: “Tam giác ABC cân và có một góc bằng 60°”, hãy phát biểu hai mệnh đề P ⇒ Q và Q ⇒ P và xác định tính đúng sai của mỗi mệnh đề đó. Nếu cả hai mệnh đề trên đều đúng, hãy phát biểu mệnh đề tương đương.

Trả lời:

+ Mệnh đề P ⇒ Q: “Nếu tam giác ABC đều thì tam giác ABC cân và có một góc bằng 60°”.

Đây là mệnh đề đúng vì tam giác đều có 3 cạnh bằng nhau và 3 góc bằng nhau và bằng 60° và tam giác cân là tam giác có 2 cạnh bằng nhau, nên tam giác đều là tam giác cân và có 1 góc bằng 60°.

+ Mệnh đề Q ⇒ P: “Nếu tam giác ABC cân và có một góc bằng 60° thì tam giác ABC đều”.

Đây là mệnh đề đúng theo dấu hiệu nhận biết tam giác đều.

Do đó cả hai mệnh đề P ⇒ Q và Q ⇒ P đều là mệnh đề đúng. Vậy ta có mệnh đề tương đương P ⇔ Q: “Tam giác ABC đều khi và chỉ khi tam giác ABC cân và có một góc bằng 60°”.

6. Kí hiệu ∀ và ∃

Hoạt động 7: Cho mệnh đề chứa biến “n chia hết cho 3” với n là số tự nhiên.

a) Phát biểu “Mọi số tự nhiên n đều chia hết cho 3” có phải là mệnh đề không?

b) Phát biểu “Tồn tại số tự nhiên n chia hết cho 3” có phải là mệnh đề không?

Trả lời:

a) Phát biểu “Mọi số tự nhiên n đều chia hết cho 3” là một phát biểu sai (vì 2 là số tự nhiên nhưng 2 không chia hết cho 3). Đây là một mệnh đề.

b) Phát biểu “Tồn tại số tự nhiên n đều chia hết cho 3” là một phát biểu đúng (chẳng số 3 là số tự nhiên và 3 chia hết cho 3). Đây là một mệnh đề.

Hoạt động 8: Bạn An nói: “Mọi số thực đều có bình phương là một số không âm”.

Bạn Bình phủ định lại câu nói của bạn An: “Có một số thực mà bình phương của nó là một số âm”.

a) Sử dụng kí hiệu “∀” để viết mệnh đề của bạn An.

b) Sử dụng kí hiệu “∃” để viết mệnh đề của bạn Bình.

Trả lời:

a) Mệnh đề của bạn An viết dưới dạng sử dụng kí hiệu: “∀ x ∈ ℝ, x2 là một số không âm”.

b) Mệnh đề của bạn Bình viết dưới dạng sử dụng kí hiệu: “∃ x ∈ ℝ, x2 là một số âm”.

Luyện tập, vận dụng 7: Phát biểu mệnh đề phủ định của mỗi mệnh đề sau:

a) Tồn tại số nguyên chia hết cho 3;

b) Mọi số thập phân đều viết được dưới dạng phân số.

Trả lời:

a) Phủ định của mệnh đề " ∃ x ∈ Z, x chia hết cho 3" là mệnh đề " ∀ x ∈ Z, x không chia hết cho 3".

b) Phủ định của mệnh đề "Mọi số thập phân đều viết được dưới dạng phân số" là mệnh đề "Tồn tại số thập phân không viết được dưới dạng phân số".

Bài tập

Bài tập 1: Trong các phát biểu sau, phát biểu nào là mệnh đề toán học?

a) Tích hai số thực trái dấu là một số thực âm.

b) Mọi số tự nhiên đều là số dương.

c) Có sự sống ngoài Trái Đất.

d) Ngày 1 tháng 5 là ngày Quốc tế Lao động.

Trả lời:

Mệnh đề toán học là một phát biểu khẳng định về một sự kiện trong toán học.

Vậy trong các phát biểu đã cho thì phát biểu a, b là các mệnh đề toán học.

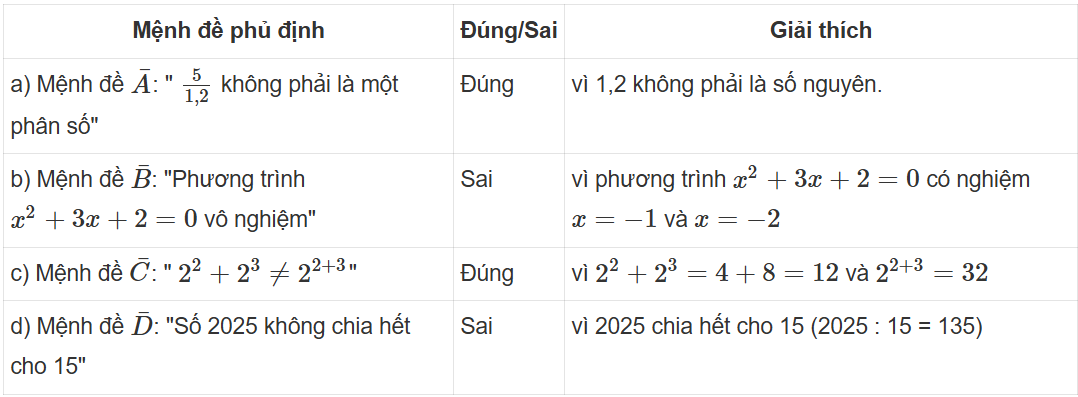
Bài tập 2: Lập mệnh đề phủ định của mỗi mệnh đề sau và nhận xét tính đúng sai của mệnh đề phủ định đó:

a) A: “ $\frac{5}{1,2}$ là một phân số”;

b) B: “Phương trình x2 + 3x + 2 = 0 có nghiệm”;

c) C: “22 + 23 = 22 + 3”;

d) D: “Số 2 025 chia hết cho 15”.

Trả lời:

Bài tập 3: Cho n là số tự nhiên. Xét hai mệnh đề:

P: “Số tự nhiên n chia hết cho 16”;

Q: “Số tự nhiên n chia hết cho 8”;

a) Với n = 32, phát biểu mệnh đề P ⇒ Q và xét tính đúng sai của mệnh đề đó.

b) Với n = 40, phát biểu mệnh đề đảo của mệnh đề P ⇒ Q và xét tính đúng sai của mệnh đề đó.

Trả lời:

a) Với n = 32, ta có các mệnh đề P, Q khi đó là:

P: “Số tự nhiên 32 chia hết cho 16”;

Q: “Số tự nhiên 32 chia hết cho 8”;

Mệnh đề P ⇒ Q: “Nếu số tự nhiên 32 chia hết cho 16 thì số tự nhiên 32 chia hết cho 8”.

Đây là mệnh đề đúng vì 32 chia hết cho 16 và 8.

b) Với n = 40, ta có các mệnh đề P, Q khi đó là:

P: “Số tự nhiên 40 chia hết cho 16”;

Q: “Số tự nhiên 40 chia hết cho 8”;

Mệnh đề đảo của mệnh đề P ⇒ Q là mệnh đề Q ⇒ P: “Nếu số tự nhiên 40 chia hết cho 8 thì số tự nhiên 40 chia hết cho 16”.

Mệnh đề đảo này là mệnh đề sai. Vì 40 chia hết cho 8 nhưng 40 không chia hết cho 16.

Bài tập 4: Cho tam giác ABC. Xét các mệnh đề:

P: “Tam giác ABC cân”;

Q: “Tam giác ABC có hai đường cao bằng nhau”.

Phát biểu mệnh đề P ⇔ Q bằng bốn cách.

Trả lời:

Phát biểu mệnh đề P ⇔ Q bằng bốn cách như sau:

Cách 1: “Tam giác ABC cân tương đương tam giác ABC có hai đường cao bằng nhau”.

Cách 2: “Tam giác ABC cân là điều kiện cần và đủ để có tam giác ABC có hai đường cao bằng nhau”.

Cách 3: “Tam giác ABC cân khi và chỉ khi tam giác ABC có hai đường cao bằng nhau”.

Cách 4: “Tam giác ABC cân nếu và chỉ nếu tam giác ABC có hai đường cao bằng nhau”.

Bài tập 5: Dùng kí hiệu “∀” hoặc “∃” để viết các mệnh đề sau:

a) Có một số nguyên không chia hết cho chính nó;

b) Mọi số thực cộng với 0 đều bằng chính nó.

Trả lời:

a) Có một số nguyên không chia hết cho chính nó;

"∃ x ∈ Z, x không chia hết cho x"

b) Mọi số thực cộng với 0 đều bằng chính nó.

"∀ y ∈ R, y+0=y"

Bài tập 6: Phát biểu các mệnh đề sau:

a) $\forall x \in ℝ$ , x2 ≥ 0;

b) $\exists x \in ℝ, \frac{1}{x} > x$ .

Trả lời:

a) Mọi số thực có bình phương không âm.

b) Có một số thực nhỏ hơn nghịch đảo của chính nó.

Bài tập 7: Lập mệnh đề phủ định của mỗi mệnh đề sau và xét tính đúng sai của mỗi mệnh đề phủ định đó:

a) $\forall x \in ℝ$ , x2 ≠ 2x – 2;

b) $\forall x \in ℝ$ , x2 ≤ 2x – 1;

c) $\exists x \in ℝ, x + \frac{1}{x} \geq 2$ ;

d) $\exists x \in ℝ$ , x2 – x + 1 < 0.

Trả lời:

a) Phủ định của mệnh đề “ $\forall x \in ℝ$ , x2 ≠ 2x – 2” là mệnh đề “ $\exists x \in ℝ$ , x2 = 2x – 2”.

Mệnh đề phủ định trên là mệnh đề sai, thật vậy ta xét phương trình x2 = 2x – 2

⇔ x2 – 2x + 2 = 0

Đây là phương trình bậc hai với ∆' = (– 1)2 – 1 . 2 = – 1 < 0

Do đó phương trình vô nghiệm trên tập số thực.

Nghĩa là x2 ≠ 2x – 2 với mọi số thực x.

Vậy mệnh đề phủ định trên là mệnh đề sai.

b) Phủ định của mệnh đề “ $\forall x \in ℝ$ , x2 ≤ 2x – 1” là mệnh đề “ $\exists x \in ℝ$ , x2 > 2x – 1”.

Mệnh đề phủ định này là mệnh đề đúng. Để chứng minh mệnh đề đúng, ta chỉ cần chỉ ra một giá trị cụ thể của x để nhận được mệnh đề đúng.

Thật vậy, chọn x = 2, ta thấy 22 = 4 và 2 . 2 – 1 = 4 – 1 = 3, vì 4 > 3 nên 22 > 2 . 2 – 1.

Vậy mệnh đề phủ định là mệnh đề đúng.

c) Phủ định của mệnh đề “ $\exists x \in ℝ, x + \frac{1}{x} \geq 2$ ” là mệnh đề “ $\forall x \in ℝ, x + \frac{1}{x} < 2$ ”.

Mệnh đề phủ định trên là mệnh đề sai. Thật vậy, ta chỉ cần lấy bất kì một giá trị x để nhận được mệnh đề sai.

Chọn x = 4, ta thấy $4 + \frac{1}{4} = 4, 25$ > 2.

Vậy mệnh đề phủ định là mệnh đề sai.

d) Phủ định của mệnh đề “ $\exists x \in ℝ$ , x2 – x + 1 < 0” là mệnh đề “ $\forall x \in ℝ$ , x2 – x + 1 ≥ 0”.

Mệnh đề phủ định này là mệnh đề đúng.

Ta có: x2 – x + 1 = $x^{2} - 2. x . \frac{1}{2} + {(\frac{1}{2})}^{2} + \frac{3}{4} = {(x - \frac{1}{2})}^{2} + \frac{3}{4} > 0 \forall x \in ℝ$ .