Giải SGK Toán 10 Cánh Diều Bài 2: Tập hợp. Các phép toán trên tập hợp - Giải SGK Toán 10 - Cánh Diều

Câu hỏi khởi động: Khái niệm tập hợp thường gặp trong toán học và trong đời sống. Chẳng hạn:

Tập hợp A các học sinh của lớp 10D.

Tập hợp B các học sinh tổ I của lớp 10D.

Làm thế nào để diễn tả quan hệ giữa tập hợp A và tập hợp B?

Trả lời:

Ta thấy các học sinh tổ I của lớp 10D đều là các học sinh của lớp 10D.

Khi đó, tập hợp B là tập con của tập hợp A, kí hiệu B ⊂ A.

Đây chính là mối quan hệ giữa hai tập hợp A và B.

1. Tập hợp

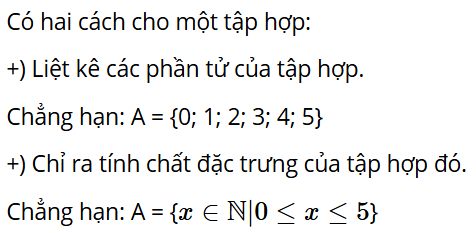
Hoạt động 1: Ở lớp 6, ta đã làm quen với khái niệm tập hợp, kí hiệu và cách viết tập hợp, phần tử thuộc tập hợp. Hãy nêu cách cho một tập hợp.

Trả lời:

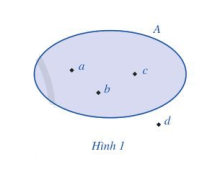
Hoạt động 2: Người ta còn minh họa tập hợp bằng một vòng kín, mỗi phần tử của tập hợp được biểu diễn bởi một chấm bên trong vòng kín, còn phần tử không thuộc tập hợp đó được biểu diễn bởi một chấm bên ngoài vòng kín (Hình 1). Cách minh họa tập hợp như vậy được gọi là biểu đồ Ven.

Hoạt động 2 trang 12 Toán 10 Tập 1 Cánh diều | Giải Toán 10

a) Viết tập hợp A trong Hình 1 bằng cách liệt kê các phần tử của tập hợp đó.

b) Nêu phần tử không thuộc tập hợp A.

Trả lời:

a) Quan sát Hình 1, ta thấy bên trong vòng kín biểu diễn tập hợp A có 3 chấm biểu diễn 3 phần tử a, b, c. Vậy ta viết tập hợp A bằng cách liệt kê các phần tử như sau:

A = {a; b; c}.

b) Nhận thấy chấm biểu diễn phần tử d nằm ngoài vòng kín biểu diễn tập hợp A, do đó phần tử d không thuộc tập hợp A, ta viết d ∉ A.

Hoạt động 3: Nêu số phần tử của mỗi tập hợp sau:

C = {x $\in ℝ$ | x2 < 0}, D = {a}, E = {b; c; d}, $ℕ =$ {0; 1; 2; …}.

Trả lời:

Luyện tập, vận dụng 1: Nêu số phần tử của mỗi tập hợp sau:

$G = \{x \in ℤ | x^{2} - 2 = 0\}$

$ℕ^{*}$ = {1; 2; 3; …}.

Trả lời:

G={x∈Z∣x2−2=0}. Tập hợp G không chứa phần tử nào.

N∗={1;2;3;...}. Tập hợp N∗ có vô số phần tử.

2. Tập con và tập hợp bằng nhau

Hoạt động 4: Cho hai tập hợp:

A = {x $\in ℤ$ | – 3 < x < 3}, B = {x $\in ℤ$ | – 3 ≤ x ≤ 3}.

a) Viết tập hợp A, B bằng cách liệt kê các phần tử của tập hợp.

b) Mỗi phần tử của tập hợp A có thuộc tập hợp B không?

Trả lời:

a) A = {x $\in ℤ$ | – 3 < x < 3}

Tập hợp A gồm các số nguyên lớn hơn – 3 và nhỏ hơn 3, đó là: – 2, – 1, 0, 1, 2.

Ta viết tập hợp A bằng cách liệt kê các phần tử như sau: A = {– 2; – 1; 0; 1; 2}.

B = {x $\in ℤ$ | – 3 ≤ x ≤ 3}

Tập hợp B gồm các số nguyên lớn hơn hoặc bằng – 3 và nhỏ hơn hoặc bằng 3, đó là: –3, – 2, – 1, 0, 1, 2, 3.

Ta viết tập hợp B bằng cách liệt kê các phần tử như sau: B = {– 3; – 2; – 1; 0; 1; 2; 3}.

b) Nhận thấy mỗi phần tử của tập hợp A đều thuộc tập hợp B.

Luyện tập, vận dụng 2: Cho hai tập hợp:

A = { $n \in ℕ$ | n chia hết cho 3},

B = { $n \in ℕ$ | n chia hết cho 9}.

Chứng tỏ rằng B ⊂ A.

Trả lời:

Lấy phần tử n tùy ý thuộc B.

Ta có n chia hết cho 9 nên n=9.k (k∈N)

mà n=9.k=3.3.k ⇒n chia hết cho 3 ⇒n∈A

Vậy B⊂A

Hoạt động 5: Cho hai tập hợp:

A = {0; 6; 12; 18}, B = {n∈ ℕ| n ≤ 18 và n là bội của 6}.

Các mệnh đề sau có đúng không?

a) A ⊂ B;

b) B ⊂ A.

Trả lời:

Luyện tập, vận dụng 3: Cho hai tập hợp E = {n $\in ℕ$ | n chia hết cho 3 và 4} và G = {n $\in ℕ$ | n chia hết cho 12}. Chứng tỏ rằng E = G.

Trả lời:

n chia hết cho 3 và 4 ⇔n chia hết cho 12 (do ƯCLN (3,4)=1) ⇒E⊂G và G⊂E

Vậy E=G

3. Giao của hai tập hợp

Hoạt động 6: Lớp trưởng lập hai danh sách cách bạn đăng kí tham gia câu lạc bộ thể thao như sau (biết trong lớp không có hai bạn nào cùng tên):

- Bóng đá gồm: An, Bình, Chung, Dũng, Minh, Nam, Phương;

- Bóng rổ gồm: An, Chung, Khang, Phong, Quang, Tuấn.

Hãy liệt kê danh sách các bạn đăng kí tham gia cả hai câu lạc bộ.

Trả lời:

Quan sát danh sách trên, ta thấy hai bạn An, Chung đều trong danh sách đăng kí tham gia câu lạc bộ bóng đá và bóng rổ.

Vậy danh sách các bạn đăng kí tham gia cả hai câu lạc bộ là: An, Chung.

4. Hợp của hai tập hợp

Hoạt động 7: Hai trường dự định tổ chức giải thi đấu thể thao cho học sinh lớp 10. Trường thứ nhất đề xuất ba môn thi đấu là: Bóng bàn, Bóng đá, Bóng rổ. Trường thứ hai đề xuất ba môn thi đấu là: Bóng đá, Bóng rổ, Cầu lông. Lập danh sách những môn thi đấu mà cả hai trường đã đề xuất.

Trả lời:

- Danh sách những môn thi đấu mà cả hai trường đã đề xuất là: Bóng bàn, Bóng đá, Bóng rổ, Cầu lông.

Luyện tập, vận dụng 4: Cho hai tập hợp:

A = {x $\in ℝ$ | x ≤ 0}, B = {x $\in ℝ$ | x ≥ 0}.

Tìm A ∩ B và A ∪ B.

Trả lời:

Tập hợp A gồm các số thực nhỏ hơn hoặc bằng 0, tập hợp B gồm các số thực lớn hơn hoặc bằng 0.

Khi đó phần tử 0 vừa thuộc tập hợp A vừa thuộc tập hợp B.

Do đó A ∩ B = {0} và A ∪ B = {x | x $\in ℝ$ } = $ℝ$ .

5. Phần bù. Hiệu của hai tập hợp

Hoạt động 8: Gọi $ℝ$ là tập hợp các số thực, I là tập hợp các số vô tỉ. Khi đó I ⊂ $ℝ$ . Tìm tập hợp những số thực không phải là số vô tỉ.

Trả lời:

- Tập hợp các số thực không phải là số vô tỉ chính là tập hợp Q các số hữu tỉ.

Hoạt động 9: Cho hai tập hợp: A = {2; 3; 5; 7; 14}, B = {3; 5; 7; 9; 11}. Liệt kê các phần tử thuộc tập hợp A nhưng không thuộc tập hợp B.

Trả lời:

- Các phần tử thuộc tập hợp A nhưng không thuộc tập hợp B là: 2; 14.

Luyện tập, vận dụng 5: Cho hai tập hợp:

A = {x $\in ℤ$ | – 2 ≤ x ≤ 3}, B = {x $\in ℝ$ | x2 – x – 6 = 0}.

Tìm A \ B và B \ A.

Trả lời:

Ta có: A={x∈Z∣−2≤x≤3}={−2;−1;0;1;2;3}

B={x∈R∣x2−x−6=0}={−2;3}

Vậy A∖B={−1;0;1;2}

và B∖A=∅

Bài tập

Bài tập 1: Cho tập hợp X = {a; b; c}. Viết tất cả các tập con của tập hợp X.

Trả lời:

Các tập hợp con của tập hợp X = {a; b; c} là: X, {a}, {b}, {c}, {a; b}, {a; c}, {b; c}.

Bài tập 2: Sắp xếp các tập hợp sau theo quan hệ “⊂”: [2; 5], (2; 5), [2; 5), (1; 5]

Trả lời:

- Thứ tự các tập hợp theo quan hệ " ⊂ " là: (2;5)⊂[2;5)⊂[2;5]⊂(1;5]

Bài tập 3: Xác định các tập hợp sau và biểu diễn chúng trên trục số:

a) [– 3; 7] ∩ (2; 5);

b) (– ∞; 0] ∪ (– 1; 2);

c) $ℝ$ \ (– ∞; 3);

d) (– 3; 2) \ [1; 3).

Trả lời:

a) Do (2; 5) ⊂ [–3 ; 7] nên giao của hai tập hợp [–3; 7] và (2; 5) là khoảng (2; 5)

Vậy [– 3; 7] ∩ (2; 5) = (2; 5) và được biểu diễn là:

Bài 3 trang 18 Toán 10 Tập 1 Cánh diều | Giải Toán 10

b) Ta có: (– ∞; 0] = {x $\in ℝ$ | x ≤ 0}

(–1 ; 2) = {x $\in ℝ$ | –1 < x < 2}

Khi đó (– ∞; 0] ∪ (–1 ; 2) = {x $\in ℝ$ | x ≤ 0 hoặc – 1 < x < 2} = {x $\in ℝ$ | x < 2} = (– ∞; 2)

Vậy (– ∞; 0] ∪ (– 1; 2) = (– ∞; 2) và được biểu diễn là:

Bài 3 trang 18 Toán 10 Tập 1 Cánh diều | Giải Toán 10

c) Tập hợp $ℝ$ \ (– ∞; 3) là tập hợp các số thực không thuộc khoảng (– ∞; 3)

Vậy $ℝ$ \ (– ∞; 3) = [3; + ∞) và được biểu diễn là:

Bài 3 trang 18 Toán 10 Tập 1 Cánh diều | Giải Toán 10

d) Tập hợp (– 3; 2) \ [1; 3) gồm các phần tử thuộc (– 3; 2) và không thuộc [1; 3).

Vậy (– 3; 2) \ [1; 3) = (– 3; 1) và được biểu diễn là:

Bài 3 trang 18 Toán 10 Tập 1 Cánh diều | Giải Toán 10

Bài tập 4: Gọi A là tập nghiệm của phương trình x2 + x – 2 = 0, B là tập nghiệm của phương trình 2x2 + x – 6 = 0.

Tìm C = A ∩ B.

Trả lời:

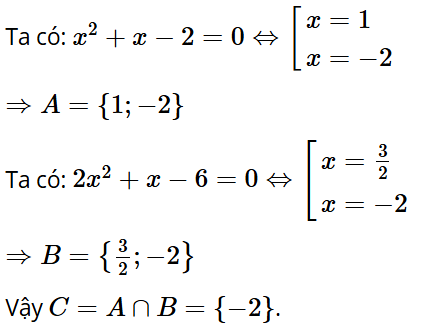
Bài tập 5: Tìm D = E ∩ G biết E và G lần lượt là tập nghiệm của hai bất phương trình trong mỗi trường hợp sau:

a) 2x + 3 ≥ 0 và – x + 5 ≥ 0;

b) x + 2 > 0 và 2x – 9 < 0.

Trả lời:

a) Ta có: 2x+3≥0⇔x≥−32

⇒ E={x∈R∣x≥−32}

Ta có: −x+5≥0⇔x≤5

⇒ G={x∈R∣x≤5}

⇒E∩G={x∈R∣−32≤x≤5}

Vậy D={x∈R∣−32≤x≤5}.

b) Ta có x+2>0⇔x>−2

⇒ E={x∈R∣x>−2}

Ta có 2x−9<0⇔x<92

⇒ E={x∈R∣x<92}

⇒E∩G={x∈R∣−2<x<92}

Vậy D={x∈R∣−2<x<92}.

Bài tập 6: Gọi A là tập nghiệm của đa thức P(x). Viết tập hợp các số thực x sao cho biểu thức $\frac{1}{P (x)}$ xác định.

Trả lời:

A là tập nghiệm của đa thức P(x).

Suy ra A = {x $\in ℝ$ | P(x) = 0}.

Biểu thức $\frac{1}{P (x)}$ xác định khi P(x) ≠ 0.

Do đó tập hợp các số thực x sao cho biểu thức $\frac{1}{P (x)}$ xác định chính là tập hợp các số thực không thuộc A.

Gọi B là tập hợp các số thực x sao cho biểu thức $\frac{1}{P (x)}$ xác định.

Vậy B = $ℝ \ A$ = $C_{ℝ} A$ .

Bài tập 7: Lớp 10B có 28 học sinh tham gia câu lạc bộ thể thao và 19 học sinh tham gia câu lạc bộ âm nhạc. Biết rằng có 10 học sinh tham gia cả hai câu lạc bộ trên.

a) Có bao nhiêu học sinh ở lớp 10B tham gia câu lạc bộ thể thao và không tham gia câu lạc bộ âm nhạc?

b) Có bao nhiêu học sinh ở lớp 10B tham gia ít nhất một trong hai câu lạc bộ trên?

c) Biết lớp 10B có 40 học sinh. Có bao nhiêu học sinh không tham giac câu lạc bộ thể thao? Có bao nhiêu học sinh không tham gia cả hai câu lạc bộ?

Trả lời:

a) Trong 28 học sinh tham gia câu lạc bộ thể thao có 10 học sinh tham gia cả câu lạc bộ âm nhạc

Vậy có 28-10=18 học sinh chỉ tham gia câu lạc bộ thể thao và không tham gia câu lạc bộ âm nhạc

b) Số học sinh tham gia ít nhất một trong hai câu lạc bộ trên là: 28 + 19 – 10 = 37 (học sinh)

c) Cả lớp có 40 học sinh, trong đó có 28 học sinh tham gia câu lạc bộ thể thao.

Do đó số học sinh không tham gia câu lạc bộ thể thao là: 40 – 28 = 12 (học sinh)

Cả lớp có 40 học sinh, trong đó có 37 học sinh tham gia ít nhất một trong hai câu lạc bộ.

Vậy số học sinh không tham gia cả hai câu lạc bộ là: 40 – 37 = 3 (học sinh)

Bài tập 8: Một nhóm có 12 học sinh chuẩn bị cho hội diễn văn nghệ. Trong danh sách đăng kí tham gia tiết mục múa và tiết mục hát của nhóm đó, có 5 học sinh tham gia tiết mục múa, 3 học sinh tham gia cả hai tiết mục. Hỏi có bao nhiêu học sinh trong nhóm tham gia tiết mục hát? Biết 4 học sinh của nhóm không tham gia tiết mục nào?

Trả lời:

Trong nhóm có 4 học sinh không tham gia tiết mục nào nên số học sinh tham gia múa và hát là:

12 – 4 = 8 (học sinh)

Trong 5 học sinh tham gia tiết mục múa có 3 học sinh tham gia cả hai tiết mục nên số học sinh chỉ tham gia tiết mục múa là:

5 – 3 = 2 (học sinh)

Số học sinh tham gia tiết mục hát là:

8 – 2 = 6 (học sinh)

Vậy trong nhóm có 6 học sinh tham gia tiết mục hát.