Câu hỏi khởi động: Hình 58 minh họa hai đoàn tàu chạy song song với vectơ vận tốc lần lượt là .
Mối liên hệ giữa hai vectơ vận tốc là như thế nào?
Trả lời:
Qua bài học này, chúng ta sẽ biết được hai vectơ vận tốc cùng phương với nhau và liên hệ với nhau theo công thức: với là các vectơ khác và số thực k ≠ 0.
I. Định nghĩa
Hoạt động 1: Gọi B là trung điểm của AC.
Chứng tỏ rằng .
Trả lời:
Do B là trung điểm của AC nên
Khi đó ta có:
Hoạt động 2: Quan sát vectơ và , nêu mối liên hệ về hướng và độ dài của vectơ với .
Trả lời:
Từ hoạt động 1, ta có:
Do đó độ dài vectơ bằng độ dài vectơ và vectơ cùng hướng với vectơ .
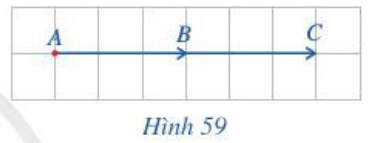
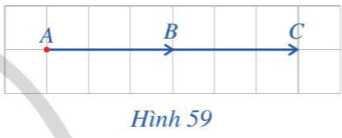
Theo quan sát trên Hình 59 ta thấy, đoạn thẳng AC dài 6 ô, còn đoạn thẳng AB dài 3 ô. Suy ra độ dài đoạn thẳng AC bằng 2 lần độ dài đoạn thẳng AB. Do đó ta có AC = 2AB hay và vectơ cùng hướng với vectơ .
Vậy vectơ cùng hướng với và .
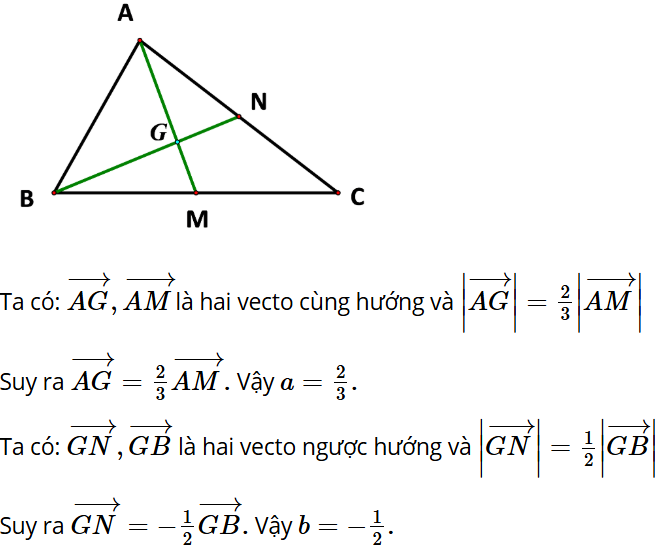
Luyện tập, vận dụng 1: Cho tam giác ABC. Hai đường trung tuyến AM và BN cắt nhau tại G. Tìm các số a, b biết: .
Trả lời:
II. Tính chất
Luyện tập, vận dụng 2: Cho ba điểm A, B, C. Chứng minh .
Trả lời:
Ta có:
→
+2BC
→
)−2(AB
→
+3BC
→
)
→
+6BC
→
−2AB
→
−6BC
→
→
III. Một số ứng dụng
Hoạt động 3: Cho I là trung điểm của đoạn thẳng AB và điểm M tùy ý. Chứng minh rằng .
Trả lời:

Luyện tập, vận dụng 3: Cho tam giác ABC có G là trọng tâm. Chứng minh .
Trả lời:

- Cách 1:
Ta có:
Cộng vế với vế:
- Cách 2:
AB−→−+AC−→−
Hoạt động 5: Cho hai vectơ và khác sao cho với k là số thực khác 0. Nêu nhận xét về phương của hai vectơ và .
Trả lời:
Ta có: với k là số thực khác 0, hai vectơ và khác .
Khi đó hai vectơ và cùng phương.
Hoạt động 6: Cho ba điểm phân biệt A, B, C.
a) Nếu ba điểm A, B, C thẳng hàng thì hai vectơ có cùng phương hay không?
b) Ngược lại, nếu hai vectơ cùng phương thì ba điểm A, B, C có thẳng hàng hay không?
Trả lời:

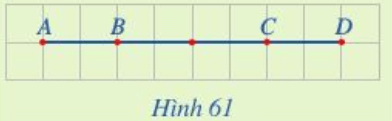
Luyện tập, vận dụng 4: Ở Hình 61, tìm k trong mỗi trường hợp sau:
a) ,
b) .
Trả lời:
a. Từ hình vẽ,
b. Từ hình vẽ,
Bài tập
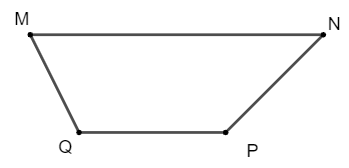
Bài tập 1: Cho hình thang MNPQ, MN // PQ, MN = 2PQ. Phát biểu nào sau đây là đúng?
A. ;
B. ;
C. ;
D. .
Đáp án: C.
MNPQ là hình thang với MN // PQ nên hai vectơ và ngược hướng.
Mà MN = 2 PQ nên .
Bài tập 2: Cho đoạn thẳng AB = 6 cm.
a) Xác định điểm C thỏa mãn .
b) Xác định điểm D thỏa mãn .
Trả lời:
a. ![]()
b. ![]()
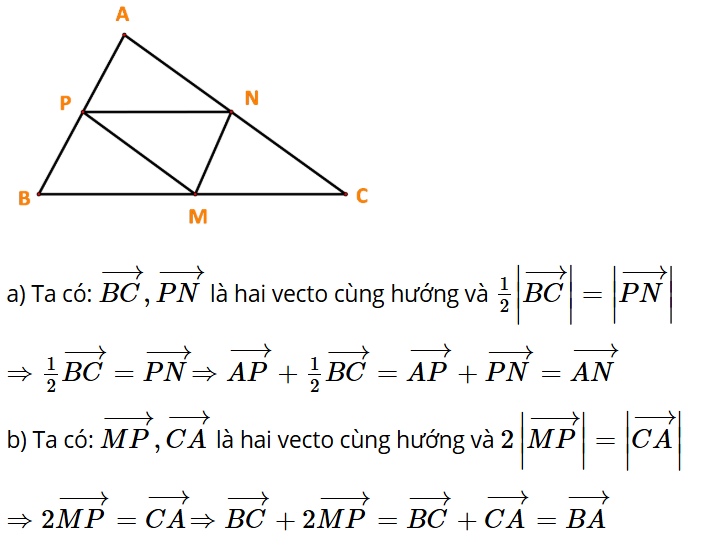
Bài tập 3: Cho tam giác ABC có M, N, P lần lượt là trung điểm của BC, CA, AB. Chứng minh:
a) ;
b) .
Trả lời:
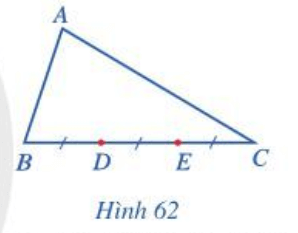
Bài tập 4: Cho tam giác ABC. Các điểm D, E thuộc cạnh BC thỏa mãn BD = DE = EC (Hình 62). Giả sử , . Biểu diễn các vectơ theo .
Trả lời:
+ Ta có:
+ BD = DE = EC và D, E thuộc cạnh BC nên BD = BC.
Mà và cùng hướng nên .
Suy ra: .
Vậy .
+ Hai vectơ cùng hướng và BE = BC nên .
Suy ra: .
Vậy .
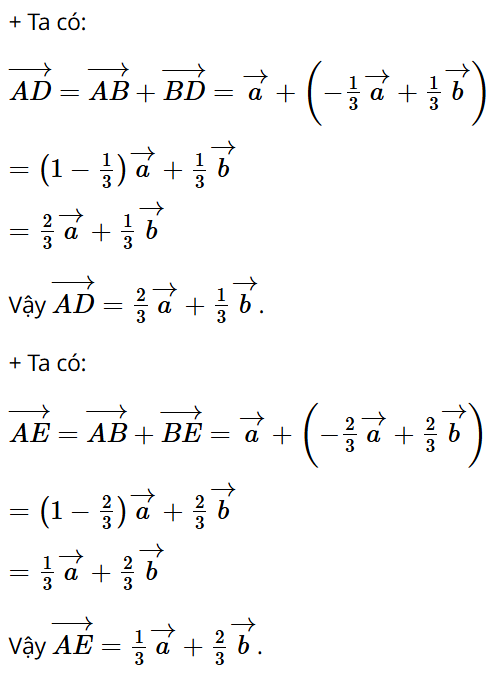
Bài tập 5: Cho tứ giác ABCD có M, N lần lượt là trung điểm của hai cạnh AB và CD. Gọi G là trung điểm của đoạn thẳng MN, E là trọng tâm của tam giác BCD. Chứng minh:
a) ;
b) ;
c) Điểm G thuộc đoạn thẳng AE và .
Trả lời:
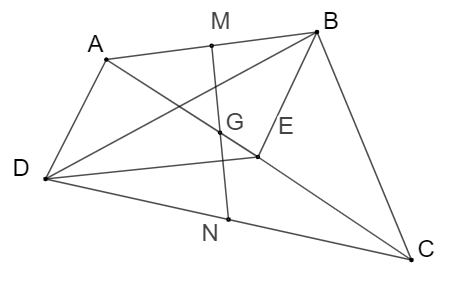
a.
b. E là trọng tâm tam giác
c. Vì
Mặt khác:
Bài tập 6: Cho hình bình hành ABCD. Đặt . Gọi G là trọng tâm của tam giác ABC. Biểu thị các vectơ theo hai vectơ .
Trả lời:

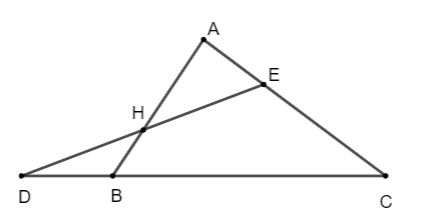
Bài tập 7: Cho tam giác ABC. Các điểm D, E, H thỏa mãn
.
a) Biểu thị mỗi vectơ theo hai vectơ .
b) Chứng minh D, E, H thẳng hàng.
Trả lời:
Vì nên và cùng hướng và .
nên cùng hướng và AE = .
nên cùng hướng và .
a)
+ Ta có
Mà .
Do đó:
.
Suy ra: .
+ Ta có:
Mà , .
Do đó:
Vậy .
+ Ta có:
Mà , .
Do đó:
Vậy .
b) Theo câu a, ta có: và .
Do đó: .
Suy ra D, H, E thẳng hàng, hơn nữa H là trung điểm của DE.