Bài tập 1: Biểu diễn miền nghiện của bất phương trình:
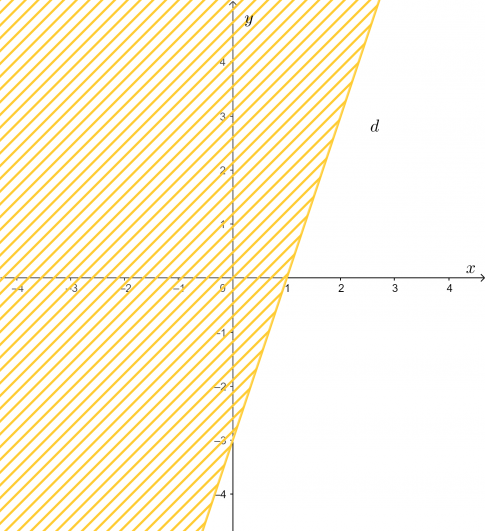
a) 3x – y > 3;
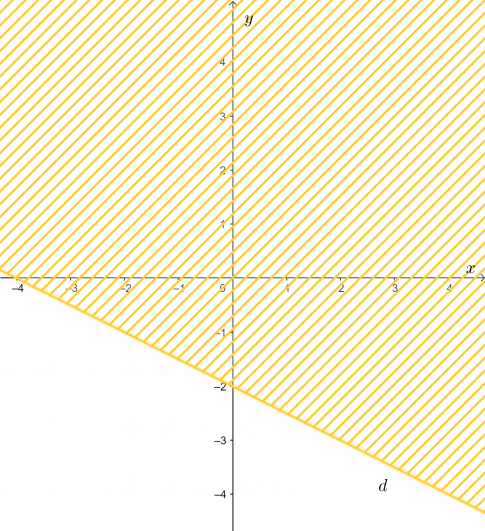
b) x + 2y ≤ – 4;
c) y ≥ 2x – 5.
Trả lời:
a.
- Vẽ đường thẳng
- Lấy điểm O(0;0). Ta có
- Vậy miền nghiệm của bất phương trình
b.
- Vẽ đường thẳng
- Lấy điểm O(0;0). Ta có
- Vậy miền nghiệm của bất phương trình
c.
- Vẽ đường thẳng
- Lấy điểm O(0;0). Ta có
- Vậy miền nghiệm của bất phương trình

Bài tập 2: Biểu diễn miền nghiệm của hệ bất phương trình:
a)
b)
c)
Trả lời:
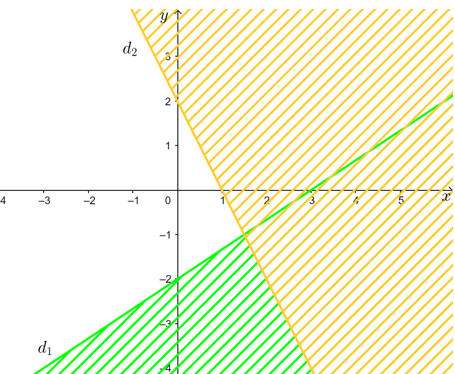
a)
+ Trên cùng một mặt phẳng tọa độ Oxy, vẽ các đường thẳng:
d1: 2x – 3y = 6;
d2: 2x + y = 2.
+ Gạch đi các phần không thuộc miền nghiệm của từng bất phương trình của hệ.
Miền nghiệm của hệ bất phương trình là phần không gạch sọc ở hình trên không kể đường thẳng d1 và d2.
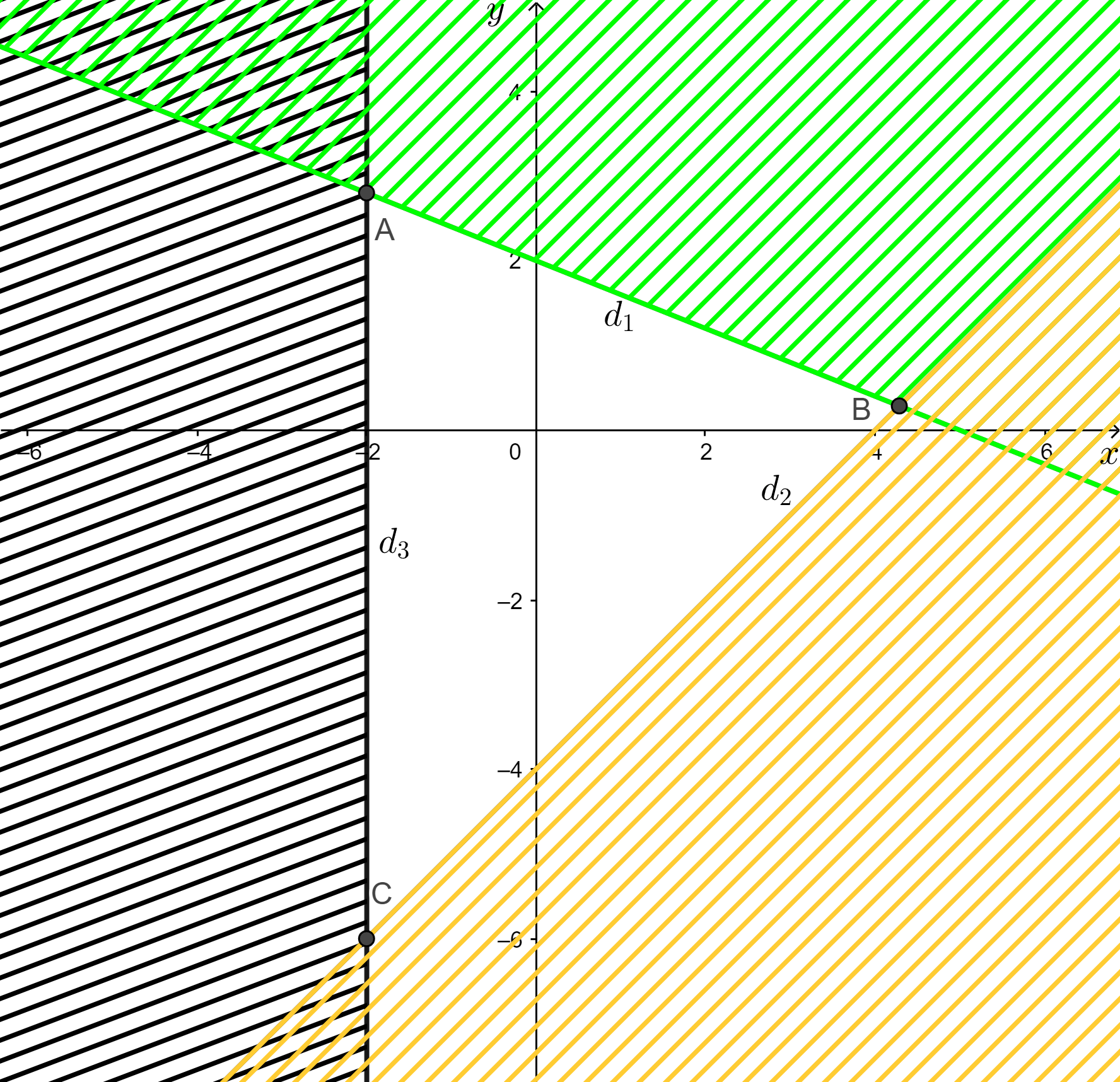
b)
+ Trên cùng một mặt phẳng tọa độ Oxy, vẽ các đường thẳng:
d1: 2x + 5y = 10;
d2: x – y = 4;
d3: x = – 2.
+ Gạch đi những phần không thuộc miền nghiệm của từng bất phương trình của hệ.
Miền nghiệm của hệ là phần không bị gạch trong hình kể cả biên.
A là giao điểm của d1 và d3 nên A(– 2; 2,8)
B là giao điểm của d1 và d2 nên
C là giao điểm của d2 và d3 nên C(– 2; – 6).
Vậy miền nghiệm của hệ bất phương trình là miền tam giác ABC.
c)
+ Trên cùng một mặt phẳng tọa độ Oxy, vẽ các đường thẳng:
d1: x – 2y = 5;
d2: x + y = 2;
d3: x = 0 là trục tung;
d4: y = 3.
+ Gạch đi những phần không thuộc miền nghiệm của từng bất phương trình của hệ.
Vậy miền nghiệm của hệ bất phương trình là miền tứ giác ABCD với A(0; 2), B(0; 3), C(11; 3), D(3; – 1).
Bài tập 3: Nhu cầu canxi tối thiểu cho một người đang độ tuổi trưởng thành trong một ngày là 1 300 mg. Trong 1 lạng đậu nành có 165 mg canxi, 1 lạng thịt có 15 mg canxi. (Nguồn: https://hongngochosspital.vn)
Gọi x, y lần lượt là số lạng đậu nành và số lạng thịt lợn mà một người đang độ tuổi trưởng thành ăn trong một ngày.
a) Viết bất phương trình bậc nhất hai ẩn x, y để biểu diễn lượng canxi cần thiết trong một ngày của một người trong độ tuổi trưởng thành.
b) Chỉ ra một nghiệm (x0; y0) với x0; y0 của bất phương trình đó.
Trả lời:
a)
Lượng canxi có trong x lạng đậu nành là 165x (mg)
Lượng canxi có trong y lạng thịt là 15y (mg)
Bất phương trình là 165x + 15y ≥ 1300
b) Thay cặp số (10;10) vào bất phương trình ta được:
165.10 + 15.10 = 1650 + 150 = 1800 > 1300
Vậy (10;10) là một nghiệm của bất phương trình.
Bài tập 4: Bác Ngọc thực hiện chế độ ăn kiêng với yêu cầu tối thiểu hằng ngày qua thức uống là 300 ca – lo, 36 đơn vị vitamin A và 90 đơn vị vitamin C. Một cốc đồ uống ăn kiêng thứ nhất cung cấp 60 ca – lo, 12 đơn vị vitamin A và 10 đơn vị vitamin C. Một cốc đồ uống ăn kiêng thứ hai cung cấp 60 ca – lo, 6 đơn vị vitamin A và 30 đơn vị vitamin C.
a) Viết hệ bất phương trình mô tả số lượng cốc cho đồ uống thứ nhất và thứ hai mà bác Ngọc nên uống mỗi ngày để đáp ứng nhu cầu cần thiết đối với số ca – lo và số đơn vị vitamin hấp thụ.
b) Chỉ ra hai phương án mà bác Ngọc có thể chọn lựa số lượng cốc cho đồ uống thứ nhất và thứ hai nhằm đáp ứng nhu cầu cần thiết đối với số ca – lo và số đơn vị vitamin hấp thụ.
Trả lời:
a) Gọi x, y lần lượt là số lượng cốc đồ uống thứ nhất và thứ hai mà bác Ngọc nên uống mỗi ngày để đáp ứng nhu cầu cần thiết đối với số ca – lo và số đơn vị vitamin hấp thụ (điều kiện x, y ).
Tổng số ca – lo mà x cốc thứ nhất và y cốc thứ hai cung cấp là: 60x + 60y (ca – lo).
Tổng số đơn vị vitamin A mà x cốc thứ nhất và y cốc thứ hai cung cấp là: 12x + 6y (đơn vị).
Tổng số đơn vị vitamin C mà x cốc thứ nhất và y cốc thứ hai cung cấp là: 10x + 30y (đơn vị).
Vì tối thiểu hằng ngày cần 300 ca – lo, 36 đơn vị vitamin A và 90 đơn vị vitamin C.
Nên ta có hệ bất phương trình sau: (I).
b) Số cốc cho đồ uống thứ nhất và thứ hai thỏa mãn yêu cầu bài toán là nghiệm của hệ (I).
+ Phương án 1: Chọn x = 1, y = 4, thay vào từng bất phương trình của hệ:
1 + 4 ≥ 5 là mệnh đề đúng;
2 . 1 + 4 ≥ 6 là mệnh đề đúng;
1 + 3. 4 ≥ 9 là mệnh đề đúng.
Vậy (1; 4) là nghiệm chung của các bất phương trình của hệ nên (1; 4) là nghiệm của hệ (I).
Do đó, bác Ngọc có thể chọn 1 cốc thứ nhất và 4 cốc thứ hai.
+ Phương án 2: Chọn x = 3, y = 4, thay vào từng bất phương trình của hệ:
3 + 4 ≥ 5 là mệnh đề đúng;
2 . 3 + 4 ≥ 6 là mệnh đề đúng;
3 + 3 . 4 ≥ 9 là mệnh đề đúng.
Vậy (3; 4) là nghiệm chung của các bất phương trình của hệ nên (3; 4) là nghiệm của hệ (I).
Do đó, bác Ngọc có thể chọn 3 cốc thứ nhất và 4 cốc thứ hai.
Bài tập 5: Một chuỗi nhà hàng ăn nhanh bán đồ ăn từ 10h00 sáng đến 22h00 mỗi ngày. Nhân viên phục vụ của nhà hàng làm việc theo hai ca, mỗi ca 8 tiếng, ca I từ 10h00 đến 18h00 và ca II từ 14h00 đến 22h00. Tiền lương của nhân viên được tính theo giờ (bảng dưới).
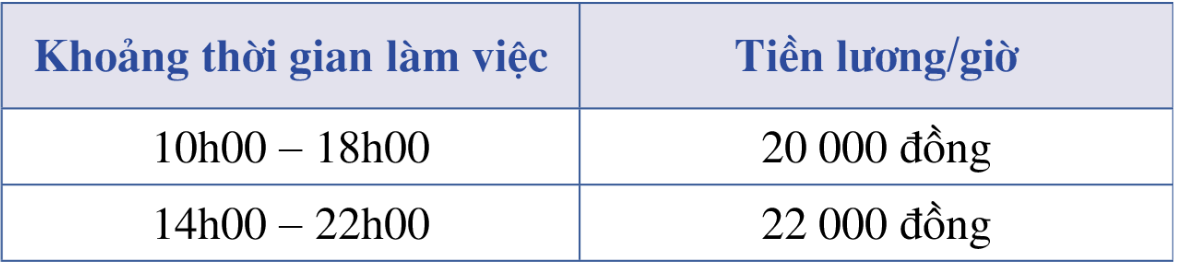
Để mỗi nhà hàng hoạt động được thì cần tối thiểu 6 nhân viên trong khoảng 10h00 – 18h00, tối thiểu 24 nhân viên trong khoảng thời gian cao điểm 14h00 – 18h00 và không quá 20 nhân viên trong khoảng 18h00 – 22h00. Do số lượng khách trong khoảng 14h00 – 22h00 thường đông hơn nên nhà hàng cần số nhân viên ca II ít nhất phải gấp đôi số nhân viên ca I. Em hãy giúp chủ chuỗi nhà hàng chỉ ra cách huy động số lượng nhân viên cho mỗi ca sao cho chi phí tiền lương mỗi ngày là ít nhất.
Trả lời:
Gọi số lượng nhân viên ca I và ca II lần lượt là
Theo bài ra ta có hệ bất phương trình:
Tổng chi phí tiền lương là:
Bài toán đưa về: Tìm
Xác định miền nghiệm của hệ bất phương trình:
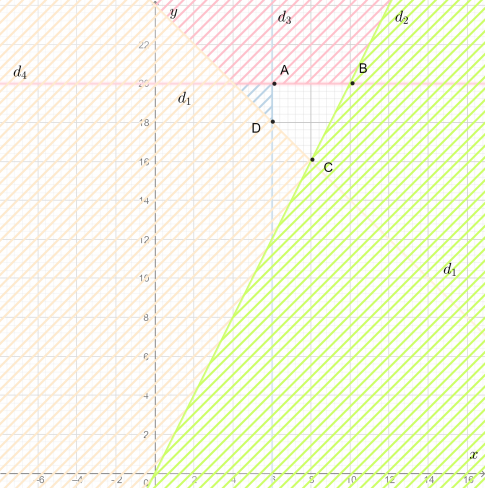
Giá trị của biểu thức
- => Vậy để tiền lương ít nhất thì ca I có 8 nhân viên, ca II có 16 nhân viên.