Giải SGK Toán 10 Cánh Diều Bài tập cuối chương I - Giải SGK Toán 10 - Cánh Diều

Bài tập 1: Phát biểu nào sau đây không là một mệnh đề toán học?

a) Tích của ba số tự nhiên liên tiếp luôn chia hết cho 3.

b) Nếu $\hat{A M B} = 90 °$ thì M nằm trên đường tròn đường kính AB.

c) Ngày 2 tháng 9 là ngày Quốc Khánh của nước Cộng hòa Xã hội chủ nghĩa Việt Nam.

d) Mọi số nguyên tố đều là số lẻ.

Trả lời:

Trong các phát biểu đã cho, có phát biểu a, b, d là các mệnh đề toán học vì nó khẳng định một sự kiện trong toán học, trong đó, phát biểu b là mệnh đề kéo theo.

Phát biểu ở câu c không phải mệnh đề toán học.

Bài tập 2: Lập mệnh đề phủ định của mỗi mệnh đề sau và xét tính đúng sai của mệnh đề phủ định đó.

A: “Đồ thị hàm số y = x là một đường thẳng”.

B: “Đồ thị hàm số y = x2 đi qua điểm A(3; 9)”.

Trả lời:

A¯: "Đồ thị hàm số y=x không phải là một đường thẳng". Mệnh đề sai vì đồ thị hàm số y=x là một đường thẳng.

B¯: "Đồ thị hàm số y=x2 đi qua điểm A(3;9)". Mệnh đề đúng vì 9=32.

Bài tập 3: Cho tứ giác ABCD. Lập mệnh đề P ⇒ Q và xét tính đúng sai của mệnh đề đó với:

a) P: “Tứ giác ABCD là hình chữ nhật”, Q: “Tứ giác ABCD là hình bình hành”;

b) P: “Tứ giác ABCD là hình thoi”, Q: “Tứ giác ABCD là hình vuông”.

Trả lời:

Bài tập 4: Lập mệnh đề phủ định của mỗi mệnh đề sau:

A: $" \forall x \in ℝ, x^{2} + 4 x + 5 \neq 0 "$ ;

B: $" \forall x \in ℝ, x^{2} + x \geq 1 "$ ;

C: “ $\exists x \in ℤ,$ 2x2 + 3x – 2 = 0”;

D: “ $\exists x \in ℤ,$ x2 < x”.

Trả lời:

+ Phủ định của mệnh đề A: $" \forall x \in ℝ, x^{2} + 4 x + 5 \neq 0 "$ là mệnh đề $A$ : $" \exists x \in ℝ, x^{2} + 4 x + 5 = 0 "$ .

+ Phủ định của mệnh đề B: $" \forall x \in ℝ, x^{2} + x \geq 1 "$ là mệnh đề $B$ : $" \exists x \in ℝ, x^{2} + x < 1 "$ .

+ Phủ định của mệnh đề C: “ $\exists x \in ℤ,$ 2x2 + 3x – 2 = 0” là mệnh đề $\bar{C}$ : “ $\exists x \in ℤ,$ 2x2 + 3x – 2 ≠ 0”.

+ Phủ định của mệnh đề D: “ $\exists x \in ℤ,$ x2 < x” là mệnh đề $\bar{D}$ : “ $\forall x \in ℤ$ , x2 ≥ x”.

Bài tập 5: Dùng kí hiệu để viết mỗi tập hợp sau và biểu diễn mỗi tập hợp đó trên trục số.

a) A = {x $\in ℝ$ | – 2 < x < – 1};

b) B = {x $\in ℝ$ | – 3 ≤ x ≤ 0};

c) C = {x $\in ℝ$ | x ≤ 1};

d) D = {x $\in ℝ$ | x > – 2}.

Trả lời:

a. Tập hợp A là khoảng (−2;−1) và được biểu diễn là:

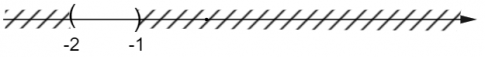
Giải Bài tập cuối chương I

b. Tập hợp B là đoạn [−3;0] và được biểu diễn là:

Giải Bài tập cuối chương I

c. Tập hợp C là nửa khoảng (−∞;1] và được biểu diễn là:

d. Tập hợp D là khoảng (−2;+∞) và được biểu diễn là:

Bài tập 6: Giải Bóng đá vô địch thế giới World Cup 2018 được tổ chức ở Liên bang Nga gồm 32 đội. Sau vòng thi đấu bảng, Ban tổ chức chọn ra 16 đội chia làm 8 cặp đấu loại trực tiếp. Sau vòng đấu loại trực tiếp đó, Ban tổ chức tiếp tục chọn ra 8 đội chia làm 4 cặp đấu loại trực tiếp ở vòng tứ kết. Gọi A là tập hợp 32 đội tham gia World Cup năm 2018, B là tập hợp 16 đội sau vòng thi đấu bảng, C là tập hợp 8 đội thi đấu vòng tứ kết.

a) Sắp xếp các tập hợp A, B, C theo quan hệ “⊂”.

b) So sánh hai tập hợp A ∩ C và B ∩ C.

c) Tập hợp A \ B gồm những đội bóng bị loại sau vòng đấu nào?

Trả lời:

Bài tập 7: Cho hai tập hợp: A = [0; 3], B = (2; + ∞).

Xác định A ∩ B, A ∪ B, A \ B, B \ A, $ℝ$ \ B.

Trả lời:

+ Tập hợp A ∩ B là tập hợp các phần tử vừa thuộc A vừa thuộc B

Vậy A ∩ B = [0; 3] ∩ (2; + ∞) = (2; 3].

+ Tập hợp A ∪ B là tập hợp các phần tử thuộc A hoặc thuộc B

Vậy A ∪ B = [0; 3] ∪ (2; + ∞) = [0; + ∞).

+ Tập hợp A \ B là tập hợp các phần tử thuộc A nhưng không thuộc B

Vậy A \ B = [0; 3] \ (2; + ∞) = [0; 2].

+ Tập hợp B \ A là tập hợp các phần tử thuộc B nhưng không thuộc A

Vậy B \ A = (2; + ∞) \ [0; 3] = (3; + ∞).

+ Tập hợp $ℝ$ \ B là tập hợp các số thực không thuộc tập hợp B

Vậy $ℝ$ \ B = $ℝ$ \ (2; + ∞) = (– ∞; 2].

Bài tập 8: Gọi E là tập nghiệm của phương trình x2 – 2x – 3 = 0, G là tập nghiệm của phương trình (x + 1)(2x – 3) = 0.

Tìm P = E ∩ G.

Trả lời:

- Ta có: x2−2x−3=0⇔(x+1)(x−3)=0⇔[x=−1x=3 ⇒E={−1;3}

- Lại có: (x+1)(2x−3)=0⇔[x=−1x=32 ⇒G={−1;32}

=> Vậy P=E∩G={−1}.