Giải SGK Toán 10 Kết nối tri thức Bài 14: Các số đặc trưng đo độ phân tán

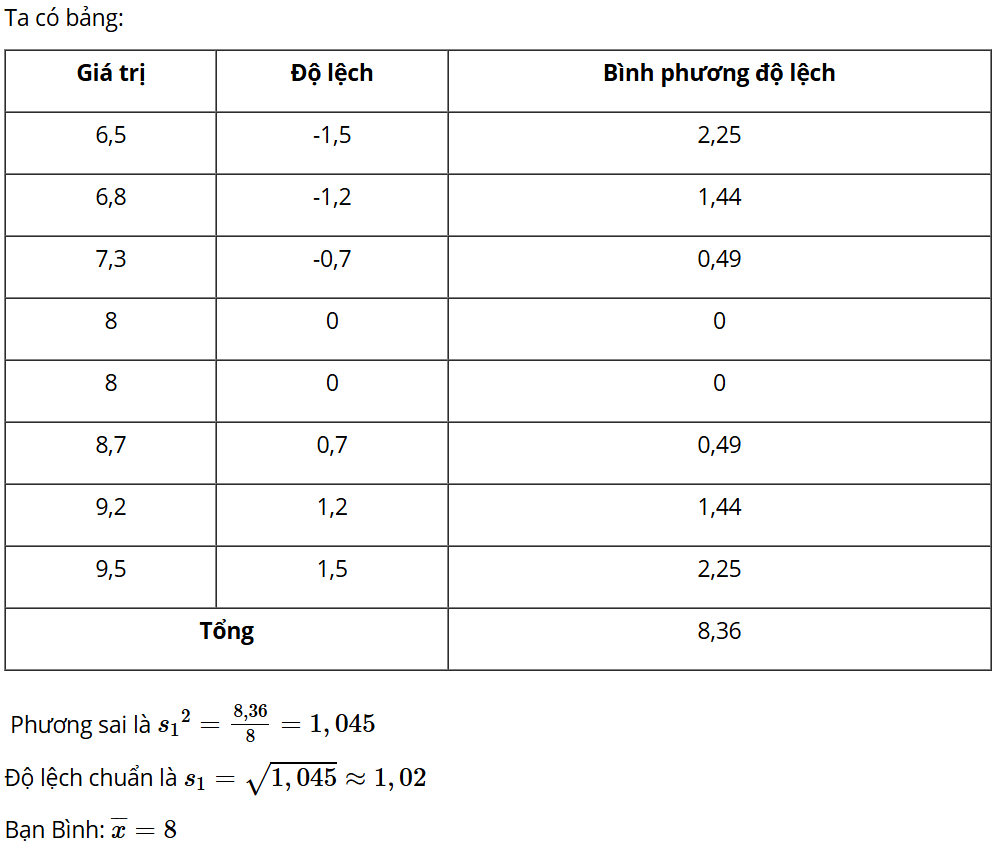
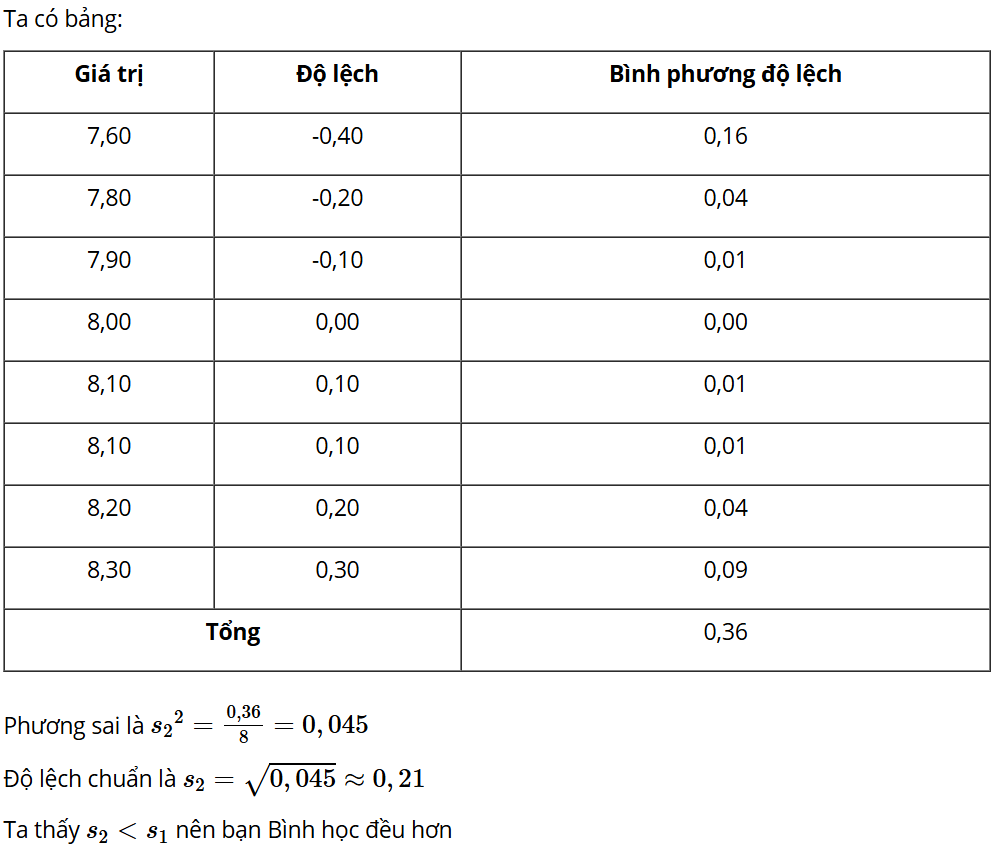
Mở đầu: Dưới đây là điểm trung bình môn học kì I của hai bạn An và Bình:

Điểm trung bình môn học kì của An và Bình đều là 8,0 nhưng rõ ràng Bình “học đều” hơn An. Có thể dùng những số đặc trưng nào để đo mức độ “học đều”?

Trả lời:

1. Khoảng biến thiên và khoảng tứ phân vị

Hoạt động 1: Một cổ động viên của câu lạc bộ Everton, Anh đã thống kê điểm số mà hai câu lạc bộ Leicester City và Everton đạt được trong năm mùa giải Ngoại hạng Anh gần đây, từ mùa giải 2014 – 2015 đến mùa giải 2018 – 2019 như sau:

Leicester City: 41   81   44   47   52.

Everton: 47   47   61   49    54.

Cổ động viên cho rằng, Everton thi đấu ổn hơn Leicester City. Em có đồng ý với nhận định này không? Vì sao?

Trả lời:

Em đồng ý với nhận định này vì:

Ở mùa giải thứ nhất, thứ ba, thứ tư và thứ năm điểm số của Everton cao hơn của Leicester.

Chỉ ở mùa giải thứ hai điểm số của Leicester City cao hơn của Everton.

Về trực quan, thành tích của Everton ổn định hơn Leicester City.

Luyện tập 1: Mẫu số liệu sau cho biết chiều cao (đơn vị cm) của các bạn trong tổ:

                                                              163  159  172  167  165  168  170  161.

Tính khoảng biến thiên của mẫu số liệu này.

Trả lời:

- Khoảng biến thiên: 172 - 159 = 13.

Hoạt động 2: Trong một tuần, nhiệt độ cao nhất trong ngày (đơn vị 0C) tại hai thành phố Hà Nội và Điện Biên được cho như sau:

Hà Nội: 23  25  28  28  32  33 35.

Điện Biên: 16  24  26  26  26  27  28.

a) Tính khoảng biến thiên của mỗi mẫu số liệu và so sánh.

b) Em có nhận xét gì về sự ảnh hưởng của giá trị 16 đến khoảng biến thiên của mẫu số liệu về nhiệt độ cao nhất trong ngày tại Điện Biên?

c) Tính các tứ phân vị và hiệu Q3 – Q1 cho mỗi mẫu số liệu. Có thể dùng hiệu này để đo độ phân tán của mẫu số liệu không?

Trả lời:

a)

Hà Nội:

Số lớn nhất là 35, số nhỏ nhất là 23

R=35-23=12

Điện Biên:

Số lớn nhất là 28, số nhỏ nhất là 16

R=28-16=12

Khoảng biến thiên về nhiệt độ của Hà Nội và Điện Biên bằng nhau.

b) Số 16 làm cho khoảng biến thiên về nhiệt độ tại Điện Biên lớn hơn.

Luyện tập 2: Mẫu số liệu sau đây cho biết số bài hát ở mỗi album trong bộ sưu tập của An:

                                                                       12  7  10  9  12  9  10  11  10  14.

Hãy tìm khoảng tứ phân vị cho mẫu số liệu này.

Trả lời:

Sắp xếp dãy số liệu theo thứ tự không giảm, ta được: 7; 9; 9; 10; 10; 10; 11; 12; 12; 14.

Mẫu số liệu gồm 10 giá trị nên trung vị bằng trung bình cộng hai giá trị chính giữa: Q2 = (10 + 10):2 = 10.

Nửa số liệu bên trái là 7; 9; 9; 10; 10 gồm 5 giá trị nên tứ phân vị thứ nhất là Q1 = 9.

Nửa số liệu bên phải là 10; 11; 12; 12; 14 gồm 5 giá trị nên tứ phân vị thứ ba là Q3 = 12.

Vậy khoảng tứ phân vị cho mẫu số liệu là: 

∆Q = Q3 – Q1 = 12 – 9 = 3.

2. Phương sai và độ lệch chuẩn

Luyện tập 3: Dùng đồng hồ đo thời gian có độ chia nhỏ nhất đến 0,001 giây để đo 7 lần thời gian rơi tự do của một vật bắt đầu từ điểm A(VA = 0) đến điểm B. Kết quả đo như sau:

                                      0,398          0,399          0,408          0,410          0,406          0,405          0,402.

(Theo Bài tập Vật lí 10, Nhà xuất bản Giáo dục Việt Nam, 2018)

Hãy tìm phương sai và độ lệch chuẩn cho mẫu số liệu này. Qua các đại lượng này, em có nhận xét gì về độ chính xác của phép đo trên?

Trả lời:

Số trung bình của mẫu số liệu là: x¯¯¯=0,398+0,399+0,408+0,41+0,406+0,405+0,4027=0,404.

Phương sai:

s2=0,0001277

s2≈0,000018

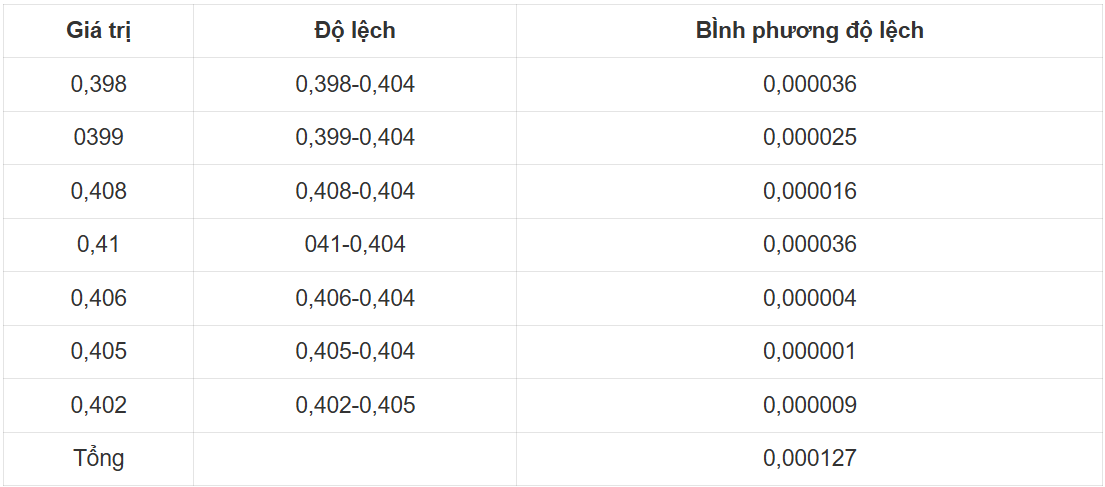
Độ lệch chuẩn: s≈0,004.

Độ chính xác của phép đo cao vì độ lệch chuẩn vầ phương sai nhỏ.

3. Phát hiện số liệu bất thường hoặc không chính xác bằng biểu đồ hộp

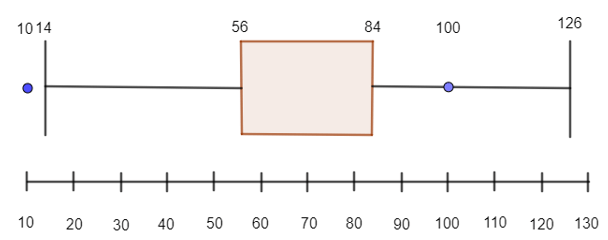
Luyện tập 4: Một mẫu số liệu có tứ phân vị thứ nhất là 56 và tứ phân vị thứ ba là 84. Hãy kiểm tra xem trong hai giá trị 10 và 100 giá trị nào được xem là giá trị bất thường.

Trả lời:

Ta cố Q1 = 56 và Q3 = 84. Do đó, khoảng tứ phân vị là:

ΔQ = 84 – 56 = 28.

Biểu đồ hộp cho mẫu số liệu này là:

Ta có: Q1 – 1,5.ΔQ = 56 – 1,5.28 = 14 và : Q3 + 1,5.ΔQ = 84 + 1,5.28 = 126 nên trong hai số liệu 10 và 100 thì giá trị được xem là bất thường là 10 (nhỏ hơn 14).

Bài tập

Bài 5.11: Mỗi khẳng định sau đúng hay sai?

(1) Nếu các giá trị của mẫu số liệu càng tập trung quanh giá trị trung bình thì độ lệch chuẩn càng lớn.

(2) Khoảng biến thiên chỉ sử dụng thông tin của giá trị lớn nhất và bé nhất , bỏ qua thông tin của các giá trị còn lại.

(3) Khoảng tứ phân vị có sử dụng thông tin của giá trị lớn nhất, giá trị bé nhất.

(4) Khoảng tứ phân vị chính là khoảng biến thiên của nửa dưới mẫu số liệu đã sắp xếp.

(5) Các số đo độ phân tán đều không âm.

Trả lời:

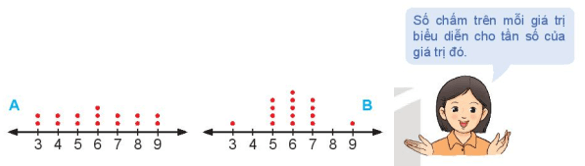
Bài 5.12: Cho hai biểu đồ chấm điểm biểu diễn hãi mẫu số liệu A, B như sau:

Không tính toán, hãy cho biết:

a) Hai mẫu số liệu này có cùng khoảng biến thiên và số trung bình không?

b) Mẫu số liệu nào có phương sai lớn hơn?

Trả lời:

a)

Mẫu số liệu thứ nhất và mẫu số liệu thứ hai có giá trị lớn nhất là 9 và giá trị nhỏ nhất là 3. Do đó hai mẫu số liệu này có cùng khoảng biến thiên.

Mẫu số liệu thứ nhất có xu hướng trung tâm là giá trị 6.

Mẫu số liệu thứ hai các giá trị tập trung nhiều xung quanh ba giá trị 5, 6, 7  nên số trung bình sẽ khoảng 6.

Do đó hai mẫu số liệu có cùng giá trị trung bình.

b)

Mẫu số liệu thứ nhất các giá trị rải đều từ 3 đến 9 nên độ phân tán nhỏ. Còn mẫu số liệu thứ hai có độ phân tán lớn hơn nên phương sai của mẫu số liệu thứ hai lớn hơn.

Bài 5.13: Cho mẫu số liệu gồm 10 số dương không hoàn toàn giống nhau. Các số đo độ phân tán (khoảng biến thiên, khoảng tứ phân vị, độ lệch chuẩn) sẽ thay đổi như thế nào nếu:

a) Nhân mỗi giá trị của mẫu số liệu với 2.

b) Cộng mỗi giá trị của mẫu số liệu với 2.

Trả lời:

a. Sự thay đổi:

• Khoảng biến thiên: gấp 2 lần.
• Khoảng tứ phân vị: gấp 2 lần.

Do mỗi giá trị tăng 2 lần, nên số trung bình cũng tăng 2 lần, nên phương sai tăng 4 lần.

Suy ra độ lệch chuẩn tăng lên 2 lần.

b. Sự thay đổi:

• Khoảng biên thiên: không đổi.
• Khoảng tứ phân vị: không đổi.

Do mỗi giá trị tăng 2 đơn vị nên số trung bình tăng (10.2) : 10 = 2 đơn vị, nhưng các giá trị cũng tăng 2 đơn vị nên độ lệch giữa giá trị và trung bình cộng không đổi, dẫn đến phương sai không đổi.

Suy ra độ lệch chuẩn không đổi. 

Bài 5.14: Từ mẫu số liệu về thuế thuốc lá của 51 thành phố tại một quốc gia, người ta tính được:

Giá trị nhỏ nhất bằng 2,5; Q1 = 36; Q2 = 60; Q3 = 100; giá trị lớn nhất bằng 205.

a) Tỉ lệ thành phố có thuế thuốc lá lớn hơn 36 là bao nhiêu?

b) Chỉ ra hai giá trị sao cho có 50% giá trị của mẫu số liệu nằm giữa hai giá trị này?

c) Tìm khoảng tứ phân vị của mẫu số liệu.

Trả lời:

a) Vì số các giá trị của số liệu n = 51 là số lẻ nên trung vị của số liệu là giá trị thứ 26.

Nửa bên trái số trung vị gồm 25 số liệu là số lẻ nên tứ phân vị thứ nhất là giá trị thứ 13 có giá trị là 36.

Do đó có 38 thành phố có thuế thuốc lá hơn 36.

Suy ra tỉ lệ các thành phố có thuế thuốc lá lớn hơn 36 là: $\frac{38}{51}=74,51\%.$

Vậy tỉ lệ các thành phố có thuế thuốc là lớn hơn 36 là: 74,51%.

b)

Tứ phân vị thứ nhất là giá trị thứ 13, tứ phân vị thứ ba là giá trị thứ 39.

Giữa hai giá trị là các giá trị thứ 13 đến giá trị thứ 39. Do đó có tất cả (39 – 13):1 + 1 = 27.

Mà $\frac{27}{51}=53\%.$

Vậy giữa hai giá trị Q1 = 36 và Q3 = 100 có 50% giá trị của mẫu số liệu nằm giữa hai giá trị này. 

d) Khoảng tứ phân vị của mẫu số liệu này là: ∆Q = Q3 – Q1 = 100 – 36 = 64

Bài 5.15: Mẫu số liệu sau đây cho biết cân nặng của 10 trẻ sơ sinh (đơn vị kg):

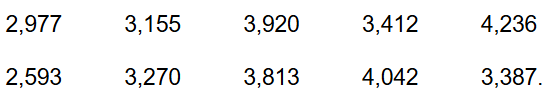
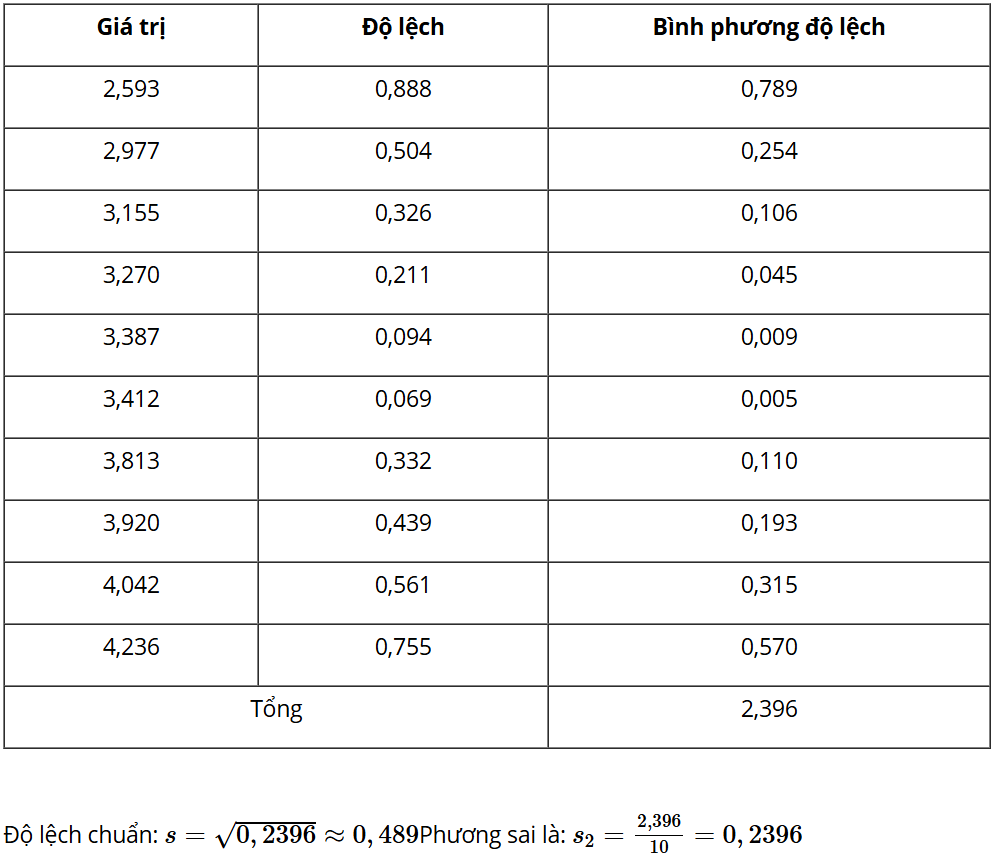
Hãy tìm khoảng biến thiên, khoảng tứ phân vị và độ lệch chuẩn cho mẫu số liệu này.

Trả lời:

Bài 5.16: Tỉ lệ thất nghiệp ở một quốc gia vào năm 2007 (đơn vị %) được cho như sau:

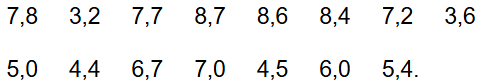
Hãy tìm các giá trị bất thường (nếu có) của mẫu số liệu trên.

Trả lời:

Sắp xếp dãy số liệu theo thứ tự không giảm, ta được: 3,2; 3,6; 4,4; 4,5; 5,0; 5,4; 6,0; 6,7; 7,0; 7,2; 7,7; 7,8; 8,4; 8,6; 8,7.

Vì n = 15 là số lẻ nên số trung vị là giá trị chính giữa Q2 = 6,7.

Nửa số liệu bên trái có 7 số liệu nên có tứ phân vị thứ nhất là Q1 = 4,5.

Nửa số liệu bên phải có 7 số liệu nên có tứ phân vị thứ hai là Q3 = 7,8.

Khoảng tứ phân vị là: ∆Q = Q3 – Q1 = 7,8 – 4,5 = 3,3. 

Ta có: Q1 – 1,5ΔQ = 4,5 – 4,95 = -0,45 và Q3 +  1,5ΔQ = 7,8 + 4,95 = 12,75 nên trong mẫu số liệu đã cho không có giá trị nào bất thường.

Vậy mẫu số liệu đã cho không có giá trị nào bất thường.