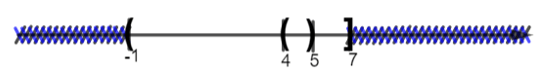A. Trắc nghiệm
Bài 1.17: Câu nào sau đây không là mệnh đề?
A. Tam giác đều là tam giác có ba cạnh bằng nhau.
B. 3 < 1.
C. 4 – 5 = 1.
D. Bạn học giỏi quá!
Đáp án: D
“Bạn học giỏi quá!” là một câu cảm thán không xác định đúng sai nên không phải là mệnh đề.
Bài 1.18: Cho định lí: “Nếu hai tam giác bằng nhau thì diện tích của chúng bằng nhau”. Mệnh đề nào sau đây là đúng?
A. Hai tam giác bằng nhau là điều kiện cần để diện tích của chúng bằng nhau.
B. Hai tam giác bằng nhau là điều kiện cần và đủ để diện tích của chúng bằng nhau.
C. Hai tam giác có diện tích bằng nhau là điều kiện đủ để chúng bằng nhau.
D. Hai tam giác bằng nhau là điều kiện đủ để diện tích của chúng bằng nhau.
Đáp án: D
Giải thích:
Từ định lí “Nếu hai tam giác bằng nhau thì diện tích của chúng bằng nhau”, ta suy ra các mệnh đề sau:
+) Hai tam giác bằng nhau là điều kiện đủ để diện tích của chúng bằng nhau.
+) Hai tam giác có diện tích bằng nhau là điều kiện cần để chúng bằng nhau.
Do đó, mệnh đề ở đáp án A và C là các mệnh đề sai, mệnh đề ở đáp án D là mệnh đề đúng.
Lại có, hai tam giác có diện tích bằng nhau thì chưa chắc hai tam giác này bằng nhau nên hai tam giác có diện tích bằng nhau không thể là điều kiện cần và đủ để chúng bằng nhau. Do đó B sai.
Bài 1.19: Mệnh đề nào sau đây là đúng?
A. ∀x ∈ ℝ, x2 > 1 ⇒ x > -1.
B. ∀x ∈ ℝ, x2 > 1 ⇒ x > 1.
C. ∀x ∈ ℝ, x > -1 ⇒ x2 > 1.
D. ∀x ∈ ℝ, x > 1 ⇒ x2 > 1.
Đáp án: D
Giải thích:
Ta có: .
Do đó mệnh đề A và mệnh đề B sai.
Với x = 0 > - 1, x2 = 0 < 1. Suy ra tồn tại một số thực x lớn hơn -1 nhưng x2 < 1. Do đó mệnh đề C sai.
Bài 1.20: Cho tập hợp A = {a; b; c}. Tập A có bao nhiêu tập con?
A. 4.
B. 6.
C. 8.
D. 10.
Đáp án: C
Giải thích:
Có 3 tập hợp con của A có một phần tử là: {a}, {b}, {c}.
Có 3 tập hợp con của A có hai phần tử là: {a; b}, {a; c}, {b; c}.
Có 1 tập hợp con của A có ba phần tử là: {a; b; c}.
Và tập ∅ cũng là tập con của tập A
Vậy tập A có tất cả 8 tập con.
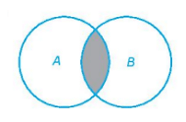
Bài 1.21: Cho các tập hợp A, B được minh họa bằng biểu đồ Ven như hình bên.
Phần tô màu xám trong hình là biểu diễn của tập hợp nào sau đây?
A. A ∩ B.
B. A\B.
C. A ∪ B.
D. B\A.
Đáp án: A
Phần tô màu xám vừa thuộc tập A cũng vừa thuộc tập B nên phần này biểu diễn cho tập hợp A ∩ B.
B. Tự luận
Bài 1.22: Biểu diễn các tập hợp sau bằng sơ đồ Ven:
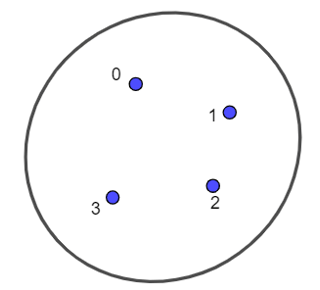
a) A = {0; 1; 2; 3};
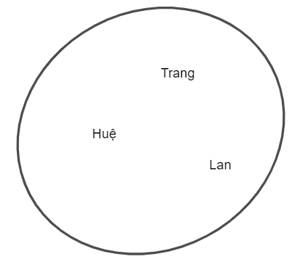
b) B = {Lan; Huệ; Trang}.
Trả lời:
a) Sơ đồ Ven biểu diễn cho tập A là:
b) Sơ đồ Ven biểu diễn cho tập B là:
Bài 1.23: Phần không bị gạch trên trục số dưới đây biểu diễn tập hợp số nào?
Trả lời:
(−∞;−2)∪[5;+∞]
Bài 1.24: Cho A = {x ∈ ℕ | x <7}; B = {1; 2; 3; 6; 7; 8}. Xác định các tập hợp sau: A ∪ B; A ∩ B; A \ B.
Trả lời:

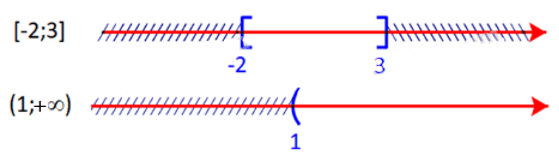
Bài 1.25: Cho hai tập hợp A = [-2; 3] và B = (1; +∞). Xác định các tập hợp sau: A ∩ B; B \ A; CℝB.
Trả lời:
Ta có:
Do đó:
+ Giao của hai tập hợp A và B là: A ∩ B = [– 2; 3] ∩ (1; + ∞) = (1; 3].
+ Hiệu của B và A là: B \ A = (1; + ∞) \ [– 2; 3] = (3; + ∞).
+ Phần bù của B trong ℝ là: CℝB = ℝ \ B = ℝ \ (1; + ∞) = (– ∞; 1].
Bài 1.26: Xác định các tập hợp sau và biểu diễn chúng trên trục số.
a) (–∞;1) ∩ (0; +∞);
b) (4;7] ∪ (–1;5);
c) (4;7] \ (–3;5].
Trả lời:
a) (–∞;1) ∩ (0; +∞) = (0;1)
Biểu diễn trên trục số, ta được:
b) (4;7] ∪ (–1;5) = (–1;7]
c) (4;7] \ (–3;5] = (5;7]
Bài 1.27: Một cuộc khảo sát về khách du lịch thăm vịnh Hạ Long cho thấy trong 1 410 khách du lịch được phỏng vấn có 789 khách du lịch đến thăm động Thiên Cung, 690 khách du lịch đến thăm đảo Titop. Toàn bộ khách được phỏng vẫn đã đến ít nhất một trong hai địa điểm trên. Hỏi có bao nhiêu khách du lịch vừa đến thăm động Thiên Cung vừa đến thăm đảo Titop ở Vịnh Hạ Long?
Trả lời:
Số khách du lịch vừa đến thăm động Thiên Cung vừa đến thăm đảo Titop ở vịnh Hạ Long là: 690 + 789 – 1410 = 69 người.