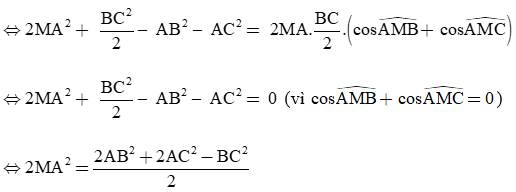Giải SGK Toán 10 Kết nối tri thức Bài tập cuối chương III

A. Trắc nghiệm

Bài 3.12: Cho tam giác ABC có $\hat{B}={135}^0$. Khẳng định nào sau đây là đúng?

a)

A. $S=\frac{1}{2}ca.$           

B. $S=\frac{-\sqrt{2}}{4}ac.$  

C. $S=\frac{\sqrt{2}}{4}bc.$

D. $S=\frac{\sqrt{2}}{4}ca.$

Đán án: D

Giải thích:

$S=\frac{1}{2}.a.c.\sin B=\frac{1}{2}a.c.\sin {135}^0=\frac{\sqrt{2}}{4}ac$.

b)

A. $R=\frac{a}{\sin A}.$

B. $R=\frac{\sqrt{2}}{2}b.$

C. $R=\frac{\sqrt{2}}{2}c.$

D. $R=\frac{\sqrt{2}}{2}a.$

Đáp án: B

Giải thích:

Ta có:

$\frac{a}{\sin A}=\frac{b}{\sin B}=\frac{c}{\sin C}=2R$ (định lí sin)

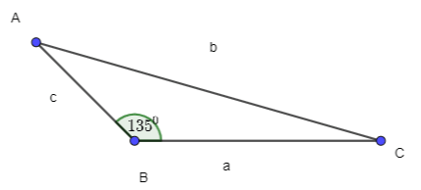
$\Rightarrow R=\frac{b}{2\sin B}=\frac{b}{2\sin {135}^0}=\frac{b}{\sqrt{2}}=\frac{\sqrt{2}}{2}b.$

c)

A. $a^2=b^2+c^2+\sqrt{2}ab$.

B. $\frac{b}{\sin A}=\frac{a}{\sin B}.$

C. $\sin B=\frac{-\sqrt{2}}{2}.$

D. b2 = c2 + a2 – 2ca.cos1350.

Đáp án: D

Giải thích:

Theo định lí cos, ta có:

b2 = a2 + c2 – 2ac.cosB = a2 + c2 – 2ac.cos1350.

Bài 3.13: Cho tam giác ABC. Khẳng định nào sau đây là đúng?

a)

A. $S=\frac{abc}{4r}.$

B. $r=\frac{2S}{a+b+c}.$

C. a2 = b2 + c2 + 2bc.cosA.

D. S = r(a + b + c).

Đáp án: B

Giải thích:

Ta có:

$S=pr=\frac{abc}{4R}=\frac{\left(a+b+c\right)r}{2}$.

Do đó A,D sai.

Theo định lí cos, ta có: a2 = b2 + c2 - 2bc.cosA. Do đó C sai.

Ta có:

$S=\frac{\left(a+b+c\right)r}{2}\Rightarrow r=\frac{2S}{a+b+c}$.

Do đó B đúng.

b)

A. sinA = sin(B + C).

B. cosA = cos(B + C).

C. cosA > 0.

D. sinA ≤ 0

Đáp án: A

Giải thích:

Ta có: 

$\hat{A}+\hat{B}+\hat{C}={180}^0\Rightarrow \hat{A}={180}^0-\left(\hat{B}+\hat{C}\right)$

$\sin \hat{A}=\sin \left[{180}^0-\left(\hat{B}+\hat{C}\right)\right]=\sin \left(\hat{B}+\hat{C}\right)$. Do đó A đúng.

$cos\hat{A}=cos\left[{180}^0-\left(\hat{B}+\hat{C}\right)\right]=-cos\left(\hat{B}+\hat{C}\right)$. Do đó B sai.

Ta có: cosA > 0 khi 00 < $\hat{A}$ < 900, mà góc A có thể là góc tù hay $\hat{A}>90°$. Do đó C sai.

Trong một tam giác, ta có: $0^0\le \hat{A}\le {180}^0$ ⇒ sin A > 0. Do đó D sai.

B. Tự luận

Bài 3.14: Tính giá trị các biểu thức sau:

a) M = sin450.cos450 + sin300;

b) $N=\sin {60}^0.cos{30}^0+\frac{1}{2}\sin {45}^0.cos{45}^0$;

c) P = 1 + tan2600;

d) $Q=\frac{1}{{\sin }^{2}120°}-{\cot }^{2}120°.$

Trả lời:

a. M = 12√.12√+12 = 1

b. N = sin60o.sin60o + 12sin 45o.sin45o

= 3√2.3√2+12.2√2.2√2 = 1

c. P = 1 + (3–√)2 = 4

d. Q = 1(3√2)2−(−13√)2 = 1

Bài 3.15: Cho tam giác ABC có $\hat{B}={60}^0,\hat{C}={45}^0,$ AC = 10. Tính a, R, S, r.

Trả lời:

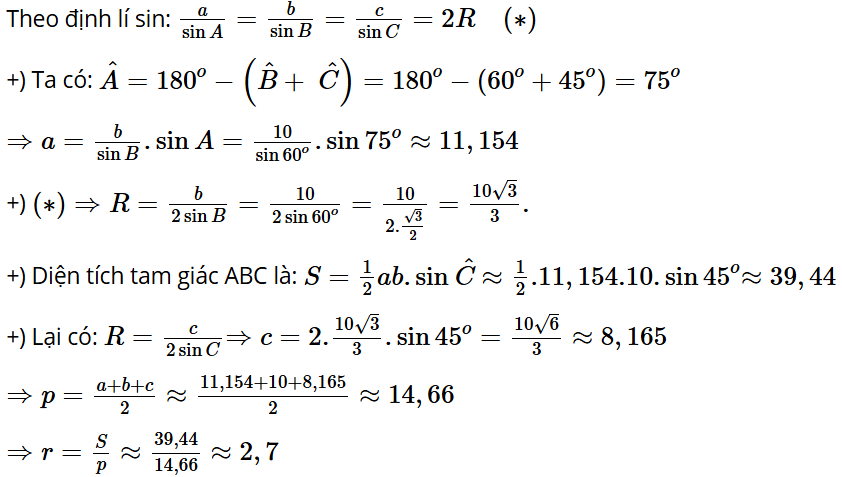
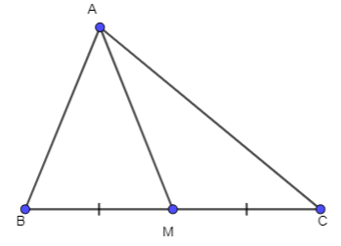
Bài 3.16: Cho tam giác ABC có trung tuyến AM. Chứng minh rằng:

a) $cos{\mathrm{AMB^\backslash widehat\{AMB\}AMB}}^{}+cos{\mathrm{AMC^\backslash widehat\{AMC\}AMC}}^{}=0;$

b) MA2 + MB2 – AB2 = 2MA.MB.cos${\mathrm{AMB^\backslash widehat\{AMB\}AMB}}^{}$ và MA2 + MC2 – AC2 = 2MA.MC.cos${\mathrm{AMC^\backslash widehat\{AMC\}AMC}}^{}$;

c) $M{A}^2=\frac{2\left(A{B}^2+A{C}^2\right)-B{C}^2}{4}$ (công thức đường trung tuyến).

Trả lời:

a) $cos{\mathrm{AMB^\backslash widehat\{AMB\}AMB}}^{}+cos{\mathrm{AMC^\backslash widehat\{AMC\}AMC}}^{}=0$

Ta có: ${\mathrm{AMB^\backslash widehat\{AMB\}AMB}}^{}+{\mathrm{AMC^\backslash widehat\{AMC\}AMC}}^{}={180}^0$

${\mathrm{AMC^\backslash widehat\{AMC\}AMC}}^{}={180}^0-{\mathrm{AMB^\backslash widehat\{AMB\}AMB}}^{}$

$cos{\mathrm{AMB^\backslash widehat\{AMB\}AMB}}^{}=-cos\left({180}^0-{\mathrm{AMB^\backslash widehat\{AMB\}AMB}}^{}\right)=-cos{\mathrm{AMC^\backslash widehat\{AMC\}AMC}}^{}$

$\Rightarrow cos{\mathrm{AMB^\backslash widehat\{AMB\}AMB}}^{}+cos{\mathrm{AMC^\backslash widehat\{AMC\}AMC}}^{}$

$=-cos{\mathrm{AMC^\backslash widehat\{AMC\}AMC}}^{}+cos{\mathrm{AMC^\backslash widehat\{AMC\}AMC}}^{}=0$

b) Xét ΔAMB, ta có:

AB2 = MA2 + MB2 – 2MA.MB.cos${\mathrm{AMB^\backslash widehat\{AMB\}AMB}}^{}$

⇔ MA2 + MB2 – AB2 = 2MA.MB.cos${\mathrm{AMB^\backslash widehat\{AMB\}AMB}}^{}$(1)

Xét ΔAMC, ta có:

AC2 = MA2 + MC2 – 2MA.MC.cos${\mathrm{AMC^\backslash widehat\{AMC\}AMC}}^{}$

⇔ MA2 + MC2 – AC2 = 2MA.MC.cos${\mathrm{AMC^\backslash widehat\{AMC\}AMC}}^{}$ (2)

c) Cộng vế với vế của (1) với (2), ta được:

MA2 + MB2 – AB2 + MA2 + MC2 – AC2 = 2MA.MB.cos${\mathrm{AMB^\backslash widehat\{AMB\}AMB}}^{}$ + 2MA.MC.cos$\widehat{AMC}$ 

$\iff 2M{A}^2+\frac{B{C}^2}{4}–A{B}^2+\frac{B{C}^2}{4}–A{C}^2$

$=2MA.\frac{BC}{2}.cos\stackrel{}{}AMB^\backslash widehat\{AMB\}AMB+2MA.\frac{BC}{2}.cos{\mathrm{AMC^\backslash widehat\{AMC\}AMC}}^{}$

(Vì $MB=MC=\frac{BC}{2}$)

$\iff M{A}^2=\frac{2\left(A{B}^2+A{C}^2\right)-B{C}^2}{4}$ (công thức đường trung tuyến).

Bài 3.17: Cho tam giác ABC. Chứng minh rằng:

a) Nếu góc A nhọn thì b2 + c2 > a2;

b) Nếu góc A tù thì b2 + c2 < a2;

c) Nếu góc A vuông thì b2 + c2 = a2.

Trả lời:

Áp dụng định lí cosin cho tam giác ABC có: 

a2=b2+c2−2bc.cosA

a. Nều góc A nhọn thì cos A > 0, suy ra: 2.b.c.cos A >0 

=> a2=b2+c2−2bc.cosA<b2+c2

b. Nếu góc A tù thì cos A < 0, suy ra: 2.b.c.cos A <0 

=> a2=b2+c2−2bc.cosA>b2+c2

c. Nếu góc A vuông thì cos A = 0, suy ra: 2.b.c.cos A =0 

=> a2=b2+c2−2bc.cosA=b2+c2 

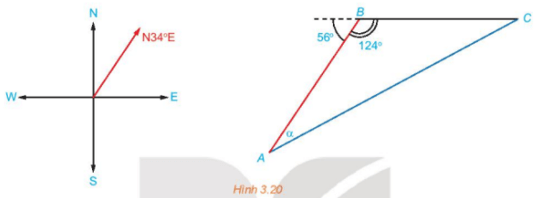
Bài 3.18: Trên biển, tàu B ở vị trí cách tàu A 53 km về hướng N34°E. Sau đó, tàu B chuyển động thẳng đều với vận tốc có độ lớn 30km/h về hướng đông và tàu A chuyển động thẳng đều với vận tốc có độ lớn 50km/h để gặp tàu B.

a) Hỏi tàu A cần phải chuyển động theo hướng nào?

b) Với hướng chuyển động đó thì sau bao lâu tàu A gặp tàu B?

Trả lời:

a) Gọi thời gian tàu A gặp tàu B ở vị trí C là x (h) (x > 0).

Vì tàu B chuyển động thẳng đều với vận tốc có độ lớn 30km/h đến C nên quãng đường BC là 30x (km).

Vì tàu A chuyển động thẳng đều với vận tốc có độ lớn 50km/h để đuổi kịp tàu B nên quãng đường AC là 50x (km).

Đặt ${\mathrm{BAC^\backslash widehat\{BAC\}BAC}}^{}=\alpha$.

Do tàu B ở vị trí cách tàu A về hướng N34°E và tàu B chạy về hướng đông nên tàu A chạy từ A theo hướng N(34 + α)°E.

Theo định lí sin trong tam giác ABC, ta có: $\frac{BC}{\sin \widehat{BAC}}=\frac{AC}{\sin \widehat{ABC}}$.

Khi đó, $\frac{30x}{\sin \alpha }=\frac{50x}{\sin 124°}$

$\iff$ α ≈ 30° hoặc α ≈ 150° (loại do tổng ba góc trong tam giác bằng 180°).

Vậy tàu A chuyển động theo hướng N64°E để gặp tàu B.

b) Xét tam giác ABC, ta có: $\hat{A}=\alpha =30°;{\mathrm{ABC^\backslash widehat\{ABC\}ABC}}^{}=124°$.

$\Rightarrow \hat{C}={180}^o-(\hat{A}+\hat{B})=180°-(30°+124°)=26°$.

Theo định lí sin, ta có: $\frac{BC}{\sin A}=\frac{AB}{\sin C}$$\Rightarrow BC=\frac{AB.\sin A}{\sin C}$

Mà BC = 30x, AB = 53, $\hat{A}=30°;\hat{C}=26°$.

Khi đó, $30x=\frac{53.\sin 30°}{\sin 26°}$ $\iff$ 30x ≈ 60 $\iff$ x ≈ 2 (giờ)

Vậy sau khoảng 2 giờ chạy theo hướng N64°E thì tàu A gặp tàu B.

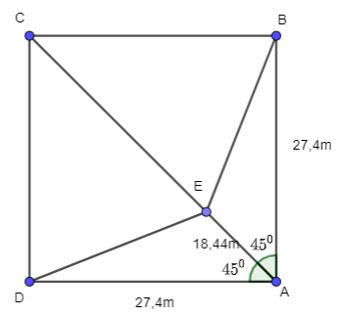
Bài 3.19: Trên sân bóng chày dành cho nam, các vị trí gôn Nhà (Home plate), gôn 1 (First base), gôn 2(Second base), gôn 3 (Third base) là bốn đỉnh của một hình vuông có cạnh dài 27,4m. Vị trí đứng ném bóng (Pitcher’s mound) nằm trên đường nối gôn Nhà với gôn 2 và cách gôn nhà 18,44m. Tính các khoảng cách từ vị trí đứng ném bóng tới các gôn 1 và gôn 3.

Trả lời: