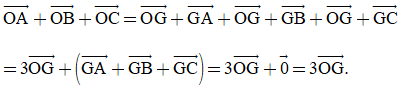Giải SGK Toán 10 Kết nối tri thức Bài 9: Tích của một vectơ với một số

1. Tích của một vectơ với một số

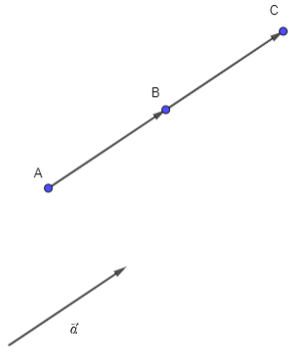
Hoạt động 1: Cho vecto $\overrightarrow{AB}=\overrightarrow{a}$. Hãy xác định điểm C sao cho $\overrightarrow{BC}=\overrightarrow{a}.$

a) Tìm mối quan hệ giữa $\overrightarrow{AB}$ và $\overrightarrow{a}+\overrightarrow{a}.$

b) Vecto $\overrightarrow{a}+\overrightarrow{a}$ có mối quan hệ như thế nào về hướng và độ dài với vecto $\overrightarrow{a}.$

Trả lời:

Xác định điểm C như sau:

Trên tia AB lấy điểm C sao cho BC = a.

a) Ta có: $\overrightarrow{a}+\overrightarrow{a}=\overrightarrow{AB}+\overrightarrow{BC}=\overrightarrow{AC}$ (quy tắc ba điểm)

Ta nhận thấy vecto $\overrightarrow{AC}$ cùng hướng với vecto $\overrightarrow{AB}$ và AC = AB + BC = 2AB.

 Suy ra $\overrightarrow{a}+\overrightarrow{a}$ cùng hướng với vecto $\overrightarrow{AB}$ và $\left|\overrightarrow{a}+\overrightarrow{a}\right|=2AB$.

b) Ta lại có: $\overrightarrow{AB}=\overrightarrow{a}$

Do đó $\overrightarrow{a}+\overrightarrow{a}$ cùng hướng với vecto $\overrightarrow{a}$ và $\left|\overrightarrow{a}+\overrightarrow{a}\right|=2\left|\overrightarrow{a}\right|$.

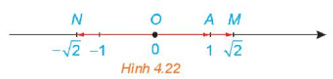
Hoạt động 2: Trên một trục số, gọi O, A, M, N tương ứng biểu thị các số $0;1;\sqrt{2};-\sqrt{2}.$ Hãy nêu mối quan hệ về  hướng và độ dài của mỗi vecto $\overrightarrow{OM},\overrightarrow{ON}$ với vecto $\overrightarrow{a}=\overrightarrow{OA}$. Viết đẳng thức thể hiện mối quan hệ giữa hai vecto $\overrightarrow{OM}$ và $\overrightarrow{OA}$.

Trả lời:

• OM−→− và a→ cùng hướng, độ dài của |OM−→−|=2–√|a→|.
• ON−→− và a→ ngược hướng, độ dài của |ON−→−|=2–√|a→|.
• OM−→−=2–√a→.

Câu hỏi: $-\overrightarrow{a}$ và $\left(-1\right)\overrightarrow{a}$ có mối quan hệ gì?

Trả lời:

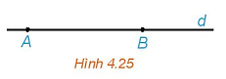
Luyện tập 1: Cho đường thẳng d đi qua hai điểm phân biệt A và B (H.4.25). Những khẳng định nào sau đây là đúng?

a) Điểm M thuộc đường thẳng d khi và chỉ khi tồn tại số t để $\overrightarrow{AM}=t\overrightarrow{AB}$.

b) Với điểm M bất kì, ta luôn có: $\overrightarrow{AM}=\frac{AM}{AB}.\overrightarrow{AB}.$

c) Điểm M thuộc tia đối của tia AB khi và chỉ khi tồn tại số t ≤ 0 để $\overrightarrow{AM}=t\overrightarrow{AB}.$

Trả lời:

a) Nếu M thuộc đường thẳng d thì $\overrightarrow{AM}$ cùng phương $\overrightarrow{AB}$

Do đó ta có tồn tại một số thực t thỏa mãn $\overrightarrow{AM}=t\overrightarrow{AB}.$

Nếu tồn tại số t thỏa mãn $\overrightarrow{AM}=t\overrightarrow{AB}$ thì $\overrightarrow{AM}$ cùng phương $\overrightarrow{AB}$ hay $\overrightarrow{AM}$ trùng với $\overrightarrow{AB}$.

Do đó A, M, B thẳng hàng hay M thuộc đường thẳng d.

Vì thế khẳng định a) đúng.

b) Nếu M không thuộc đường thẳng d thì $\overrightarrow{AM}$ và $\overrightarrow{AB}$ không cùng phương. Do đó $\overrightarrow{AM}\ne \frac{AM}{AB}\overrightarrow{AB}.$

Vì vậy khẳng định b) sai.

c) Nếu điểm M thuộc tia đối của tia AB:

Thì ta có: $\overrightarrow{MA}=t\overrightarrow{MB}$ với t < 0.

Do đó khẳng định c) sai.

2. Các tính chất của phép nhân vectơ với một số

Hoạt động 3: Với $\overrightarrow{u}\ne \overrightarrow{0}$ và hai số thực k, t, những khẳng định nào sau đây là đúng?

a) Hai vecto $k\left(t\overrightarrow{u}\right)$ và $\left(kt\right)\overrightarrow{u}$ có cùng độ dài bằng $\left|kt\right|\left|\overrightarrow{u}\right|.$

b) Nếu kt ≥ 0 thì cả hai vecto $k\left(t\overrightarrow{u}\right),\left(kt\right)\overrightarrow{u}$cùng hướng với $\overrightarrow{u}$.

c) Nếu kt < 0 thì cả hai vecto $k\left(t\overrightarrow{u}\right),\left(kt\right)\overrightarrow{u}$ ngược hướng với $\overrightarrow{u}$.

d) Hai vecto $k\left(t\overrightarrow{u}\right)$ và $\left(kt\right)\overrightarrow{u}$ bằng nhau.

Trả lời:

Khẳng định đúng: a, b, c, d.

Hoạt động 4: Hãy chỉ ra trên Hình 4.25 hai vecto $3\left(\overrightarrow{u}+\overrightarrow{v}\right)$ và $3\overrightarrow{u}+3\overrightarrow{v}$. Từ đó, nêu mối quan hệ giữa $3\left(\overrightarrow{u}+\overrightarrow{v}\right)$ và $3\overrightarrow{u}+3\overrightarrow{v}$.

Trả lời:

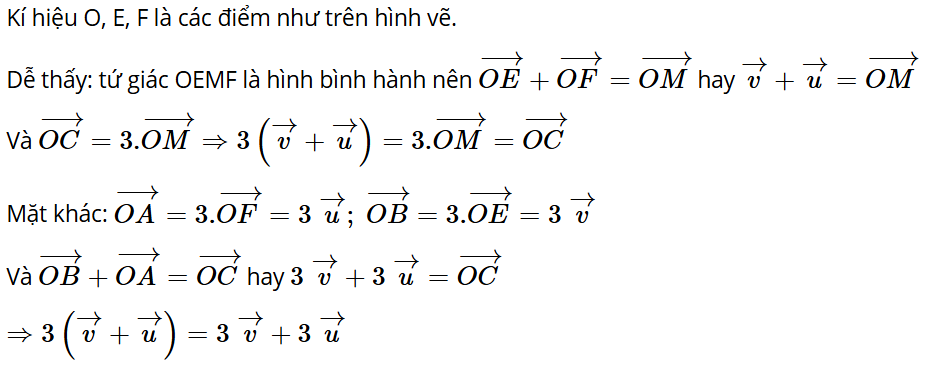
Luyện tập 2: Cho tam giác ABC có trọng tâm G. Chứng minh với điểm O tùy ý, ta có:

$\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}=3\overrightarrow{OG}$

Trả lời:

Vì G là trọng tâm tam giác ABC nên ta có:

$\overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GC}=\overrightarrow{0}$.

Do đó:

Vậy $\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}=3\overrightarrow{OG}.$

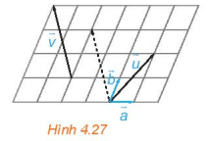
Luyện tập 3: Trong Hình 4.27, hãy biểu thị mỗi vecto $\overrightarrow{u},\overrightarrow{v}$ theo hai vecto $\overrightarrow{a},\overrightarrow{b}$, tức là tìm các số x, y, z, t để $\overrightarrow{u}=x\overrightarrow{a}+y\overrightarrow{b},\overrightarrow{v}=t\overrightarrow{a}+z\overrightarrow{b}.$

Trả lời:

• u→=2a→+2b→,
• v→=−2a→+3b→. 

Bài tập

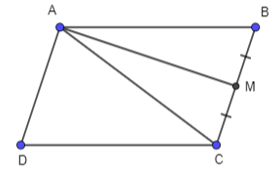
Bài 4.11: Cho hình bình hành ABCD. Gọi M là trung điểm cạnh BC. Hãy biểu thị $\overrightarrow{AM}$ theo hai vecto $\overrightarrow{AB}$ và $\overrightarrow{AD}.$

Trả lời:

Ta có hình vẽ sau:

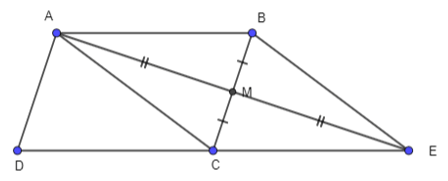
Gọi E là điểm đối xứng với A qua M. Khi đó ABEC là hình bình hành

Ta có: $\overrightarrow{AB}+\overrightarrow{AC}=\overrightarrow{AE}$ (quy tắc hình bình hành)

Mà $\overrightarrow{AE}=2\overrightarrow{AM}$

$\Rightarrow \overrightarrow{AM}=\frac{\overrightarrow{AB}+\overrightarrow{AC}}{2}$

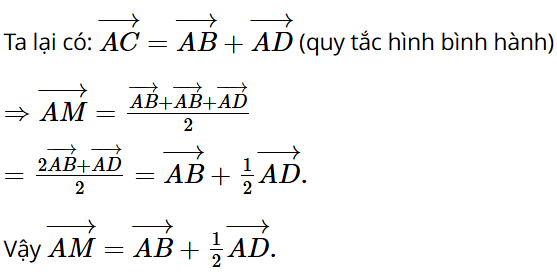
Bài 4.12: Cho tứ giác ABCD. Gọi M, N tương ứng là trung điểm của các cạnh AB, CD. Chứng minh rằng

$\overrightarrow{BC}+\overrightarrow{AD}=2\overrightarrow{MN}=\overrightarrow{AC}+\overrightarrow{BD}.$

Trả lời:

Vì N là trung điểm của CD nên ta có: NC−→−+ND−→−=0→

=> MC−→−−MN−→−+MD−→−−MN−→−=0→

=> 2MN−→−=MC−→−+MD−→−

• 2MN−→−=MC−→−+MD−→−

=> 2MN−→−=MB−→−+BC−→−+MA−→−+AD−→−

=BC−→−+AD−→−

• BC−→−+AD−→−= AC−→−−AB−→−+AB−→−+BD−→−

= AC−→−+BD−→−

Vậy BC−→−+AD−→−=2MN−→−=AC−→−+BD−→−

Bài 4.13: Cho hai điểm phân biệt A và B.

a) Hãy xác định điểm K sao cho $\overrightarrow{KA}+2\overrightarrow{KB}=\overrightarrow{0}.$

b) Chứng minh rằng với mọi điểm O, ta có: $\overrightarrow{OK}=\frac{1}{3}\overrightarrow{OA}+\frac{2}{3}\overrightarrow{OB}.$

Trả lời:

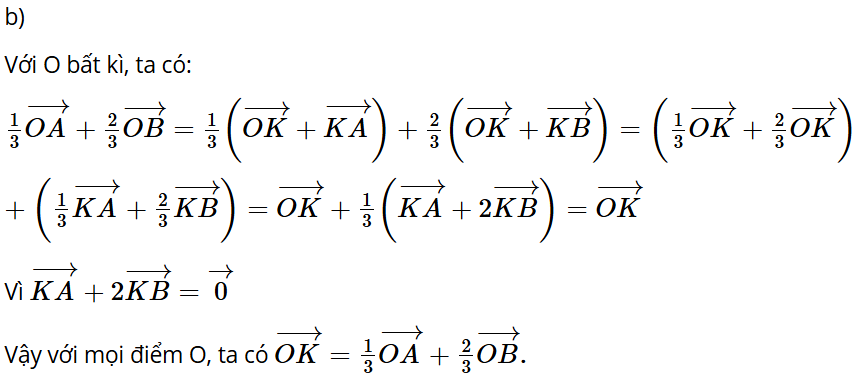
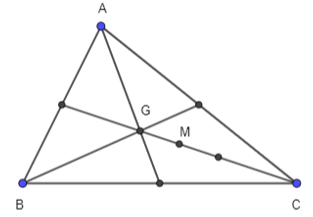
Bài 4.14: Cho tam giác ABC.

a) Hãy xác định điểm M để $\overrightarrow{MA}+\overrightarrow{MB}+2\overrightarrow{MC}=\overrightarrow{0}.$

b) Chứng minh rằng với mọi điểm O, ta có:

$\overrightarrow{OA}+\overrightarrow{OB}+2\overrightarrow{OC}=4\overrightarrow{OM}.$

Trả lời:

a) Gọi G là trọng tâm tam giác ABC, có:

$\overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GC}=\overrightarrow{0}$.

Xét $\overrightarrow{MA}+\overrightarrow{MB}+2\overrightarrow{MC}=\overrightarrow{0}$

$\iff \overrightarrow{MG}+\overrightarrow{GA}+\overrightarrow{MG}+\overrightarrow{GB}+2\overrightarrow{MG}+2\overrightarrow{GC}=\overrightarrow{0}$

$\iff 4\overrightarrow{MG}+\left(\overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GC}\right)+\overrightarrow{GC}=\overrightarrow{0}$

$\iff 4\overrightarrow{MG}+\overrightarrow{GC}=\overrightarrow{0}$

$\iff \overrightarrow{MG}=\frac{1}{4}\overrightarrow{CG}$

Suy ra điểm M nằm giữa C và G sao cho $MG=\frac{1}{4}CG.$

b) Ta có: 

$VT=\overrightarrow{OA}+\overrightarrow{OB}+2\overrightarrow{OC}$

$=\overrightarrow{OM}+\overrightarrow{MA}+\overrightarrow{OM}+\overrightarrow{MB}+2\overrightarrow{OM}+2\overrightarrow{MC}$

$=4\overrightarrow{OM}+\left(\overrightarrow{MA}+\overrightarrow{MB}+2\overrightarrow{MC}\right)$

$=4\overrightarrow{OM}=VP.$

(DO $\overrightarrow{MA}+\overrightarrow{MB}+2\overrightarrow{MC}=\overrightarrow{0}$)

Bài 4.15: Chất điểm A chịu tác động của ba lực $\overrightarrow{F_1},\overrightarrow{F_2},\overrightarrow{F_3}$ như Hình 4.30 và ở trạng thái cân bằng (tức là $\overrightarrow{F_1}+\overrightarrow{F_2}+\overrightarrow{F_3}=\overrightarrow{0}$). Tính độ lớn của các lực $\overrightarrow{F_2},\overrightarrow{F_3},$ biết $\overrightarrow{F_1}$ có độ lớn là 20N.

Trả lời:

Gọi các vecto F1−→,F2−→,F3−→ lần lượt là các vecto AC−→−,AB−→−,AD−→−.

Kẻ hình bình hành ABED thì F2−→,F3−→=AE−→−.

mà F2−→,F3−→=−F1−→.

=> |AE−→−|=|F1−→| =20N

• Xét hình bình hành ABED có: góc ABE = 180o - 120o = 60o
• Xét tam giác AEB vuông tại A có: AB = AE: tan B = 20: tan60o  ≈11,5
• Xét tam giác AED vuông tại E có: AD = AE: sin D = 20 : sin60o  ≈23

Vậy độ lớn các lực F2−→,F3−→ lần lượt là: 11,5 N và 23 N.