Giải SGK Toán 10 Kết nối tri thức Bài tập cuối chương IV

A. Trắc nghiệm

Bài 4.27: Trong mặt phẳng tọa độ, cặp vecto nào sau đây có cùng phương?

A. $\overrightarrow{u}\left(2;3\right)$ và $\overrightarrow{v}\left(\frac{1}{2};6\right)$.

B. $\overrightarrow{a}\left(\sqrt{2};6\right)$ và $\overrightarrow{b}\left(1;3\sqrt{2}\right)$.

C. $\overrightarrow{i}\left(0;1\right)$ và $\overrightarrow{j}\left(1;0\right)$.

D. $\overrightarrow{c}\left(1;3\right)$ và $\overrightarrow{d}\left(2;-6\right)$.

Đáp án: B

Giải thích:

Hai vecto $\overrightarrow{u}$ và $\overrightarrow{v}$ là hai vecto không cùng phương vì $\frac{2}{\frac{1}{2}}\ne \frac{3}{6}$. Do đó A sai.

Hai vecto $\overrightarrow{a}$ và $\overrightarrow{b}$ là hai vecto cùng phương vì $\frac{\sqrt{2}}{1}=\frac{6}{3\sqrt{2}}=\sqrt{2}$. Do đó B đúng.

Hai vecto $\overrightarrow{i}$ và $\overrightarrow{j}$ là hai vecto không cùng phương vì $\frac{0}{1}\ne \frac{1}{0}$ và $\frac{1}{0}$ không tồn tại. Do đó C sai.

Hai vecto $\overrightarrow{c}$ và $\overrightarrow{d}$ là hai vecto không cùng phương vì $\frac{1}{2}\ne \frac{3}{-6}$. Do đó D sai.

Bài 4.28: Trong mặt phẳng tọa độ, cặp vecto nào sau đây vuông góc với nhau?

A. $\overrightarrow{u}\left(2;3\right)$ và $\overrightarrow{v}\left(4;6\right)$.

B. $\overrightarrow{a}\left(1;-1\right)$ và $\overrightarrow{b}\left(-1;1\right)$.

C. $z\left(a;b\right)$ và $\overrightarrow{t}\left(-b;a\right)$.

D. $\overrightarrow{n}\left(1;1\right)$ và $\overrightarrow{k}\left(2;0\right)$.

Đáp án: C

Giải thích:

Ta có: $\overrightarrow{u}.\overrightarrow{v}$ = 2.4 + 3.6 = 8+18 = 26 ≠ 0. Suy ra hai vecto $\overrightarrow{u},\overrightarrow{v}$ không vuông góc. Do đó A sai.

Ta có: $\overrightarrow{a}.\overrightarrow{b}$ = 1.(–1) + (–1).1 = –1 + (–1) = –2 ≠ 0. Suy ra hai vecto $\overrightarrow{a},\overrightarrow{b}$ không vuông góc với nhau. Do đó B sai.

Ta có: $\overrightarrow{z}.\overrightarrow{t}$ = a.(–b) + b.a = –ab + ab = 0. Suy ra hai vecto $\overrightarrow{z},\overrightarrow{t}$ vuông góc với nhau. Do đó C đúng.

Ta có: $\overrightarrow{n}.\overrightarrow{k}$ = 1.2 + 1.0 = 2 +0 = 2 ≠ 0.Suy ra hai vecto $\overrightarrow{n},\overrightarrow{k}$ không vuông góc. Do đó D sai.

Bài 4.29: Trong mặt phẳng tọa độ, vecto nào sau đây có độ dài bằng 1?

A. $\overrightarrow{a}\left(1;1\right)$

B. $\overrightarrow{b}\left(1;-1\right)$

C. $\overrightarrow{c}\left(2;\frac{1}{2}\right)$

D. $\overrightarrow{d}\left(\frac{1}{\sqrt{2}};\frac{-1}{\sqrt{2}}\right)$

Đáp án: D

Giải thích:

Vì $\overrightarrow{a}\left(1;1\right)\Rightarrow \left|\overrightarrow{a}\right|=\sqrt{1^2+1^2}=\sqrt{2}\ne 1$. Do đó A sai.

Vì $\overrightarrow{b}\left(1;-1\right)$

$\Rightarrow \left|\overrightarrow{b}\right|=\sqrt{1^2+{\left(-1\right)}^2}=\sqrt{2}\ne 1$. Do đó B sai.

Vì $\overrightarrow{c}\left(2;\frac{1}{2}\right)$

$\Rightarrow \left|\overrightarrow{c}\right|=\sqrt{2^2+{\left(\frac{1}{2}\right)}^2}=\sqrt{\frac{17}{4}}\ne 1$. Do đó C sai.

Vì $\overrightarrow{d}\left(\frac{1}{\sqrt{2}};\frac{-1}{\sqrt{2}}\right)$

$\Rightarrow \left|\overrightarrow{d}\right|=\sqrt{{\left(\frac{1}{\sqrt{2}}\right)}^2+{\left(\frac{-1}{\sqrt{2}}\right)}^2}=1$. Do đó D đúng.

Bài 4.30: Góc giữa vecto $\overrightarrow{a}\left(1;-1\right)$ và vecto $\overrightarrow{b}\left(-2;0\right)$ có số đo bằng:

A. 900.

B. 00.

C. 1350.

D. 450.

Đáp án: C

Giải thích:

Ta có: $\overrightarrow{a}.\overrightarrow{b}=1.\left(-2\right)+\left(-1\right).0=-2,\left|\overrightarrow{a}\right|$

$=\sqrt{1^2+{\left(-1\right)}^2}=\sqrt{2},\left|\overrightarrow{b}\right|=\sqrt{{\left(-2\right)}^2+0^2}=2.$

$\Rightarrow cos\left(\overrightarrow{a}.\overrightarrow{b}\right)=\frac{\overrightarrow{a}.\overrightarrow{b}}{\left|\overrightarrow{a}\right|.\left|\overrightarrow{b}\right|}=\frac{-2}{2\sqrt{2}}=-\frac{1}{\sqrt{2}}$

$\Rightarrow \left(\overrightarrow{a}.\overrightarrow{b}\right)={135}^0.$

Bài 4.31: Khẳng định nào sau đây là đúng?

A. $\left(\overrightarrow{a}.\overrightarrow{b}\right)\overrightarrow{c}=\overrightarrow{a}\left(\overrightarrow{b}.\overrightarrow{c}\right).$

B. ${\left(\overrightarrow{a}.\overrightarrow{b}\right)}^2={\overrightarrow{a}}^2.{\overrightarrow{b}}^2.$

C. $\overrightarrow{a}.\overrightarrow{b}=\left|\overrightarrow{a}\right|.\left|\overrightarrow{b}\right|.\sin \left(\overrightarrow{a},\overrightarrow{b}\right).$

D. $\overrightarrow{a}\left(\overrightarrow{b}-\overrightarrow{c}\right)=\overrightarrow{a}.\overrightarrow{b}-\overrightarrow{a}.\overrightarrow{c}.$

Đáp án: D

Giải thích:

Theo tính chất của tích vô hướng ta có:

$\overrightarrow{a}\left(\overrightarrow{b}-\overrightarrow{c}\right)=\overrightarrow{a}.\overrightarrow{b}-\overrightarrow{a}.\overrightarrow{c}$ (tính chất phân phối đối với phép trừ)

Bài 4.32: Cho hình vuông ABCD có cạnh a. Khẳng định nào sau đây là đúng?

A. $\left(\overrightarrow{AB},\overrightarrow{BD}\right)={45}^0.$

B. $\left(\overrightarrow{AC},\overrightarrow{BC}\right)={45}^0$ và $\overrightarrow{AC}.\overrightarrow{BC}=a^2.$

C. $\overrightarrow{AC}.\overrightarrow{BD}=a^2\sqrt{2}.$

D. $\overrightarrow{BA}.\overrightarrow{BD}=-a^2.$

Đáp án: B

Giải thích:

Lấy các điểm E, F sao cho ABDE, ABFC là các hình bình hành.

Vì ABDE là hình bình hành nên $\overrightarrow{BD}=\overrightarrow{AE}$

$\Rightarrow \left(\overrightarrow{AB},\overrightarrow{BD}\right)=\left(\overrightarrow{AB},\overrightarrow{AE}\right)=\widehat{BAE}={135}^0.$ Do đó A sai.

Vì ABFC là hình bình hành nên $\overrightarrow{AC}=\overrightarrow{BF}$

$\Rightarrow \left(\overrightarrow{AC},\overrightarrow{BC}\right)=\left(\overrightarrow{BF},\overrightarrow{BC}\right)=\widehat{CBF}={45}^0$

$\Rightarrow \overrightarrow{AC}.\overrightarrow{BC}=AC.BC.cos\widehat{CBF}$

$=\sqrt{2}a.a.c{\text{os45}}^0=a^2.$ Do đó B đúng.

Ta có AC ⊥ BD $\Rightarrow \overrightarrow{AC}.\overrightarrow{BD}=0$. Do đó C sai.

Ta có: $\overrightarrow{BA}.\overrightarrow{BD}=BA.BD.\cos \left(\overrightarrow{BA},\overrightarrow{BD}\right)$

$=BA.BD.\cos \widehat{BAD}=a.a\sqrt{2}.c{\text{os45}}^0=a^2.$ Do đó D sai.

B. Tự luận

Bài 4.33: Trên cạnh BC của tam giác ABC lấy điểm M sao cho MB = 3MC.

a) Tìm mối liên hệ giữa hai vecto $\overrightarrow{MB}$ và $\overrightarrow{MC}$.

b) Biểu thị vecto $\overrightarrow{AM}$ theo hai vecto $\overrightarrow{AB}$ và $\overrightarrow{AC}.$

Trả lời:

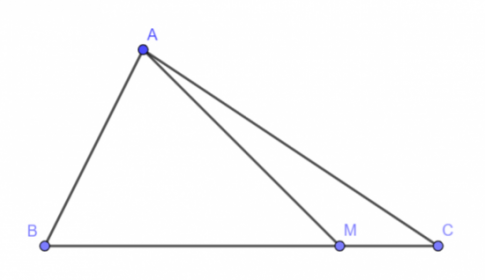
a. Do MB = 3MC, M nằm trên cạnh BC nên hai vecto MB−→− và MC−→− ngược hướng nhau nên ta có: MB−→−=−3MC−→−

b. Theo a ta có: MB−→−=−3MC−→−

=> AB−→−−AM−→−=−3.(AC−→−−AM−→−)

⇔AB−→−+3AC−→−=4AM−→−

⇔AM−→−=14AB−→−+34AC−→−.

Bài 4.34: Cho hình bình hành ABCD. Chứng minh rằng với mọi điểm M, ta có:

$\overrightarrow{MA}+\overrightarrow{MC}=\overrightarrow{MB}+\overrightarrow{MD}$

Trả lời:

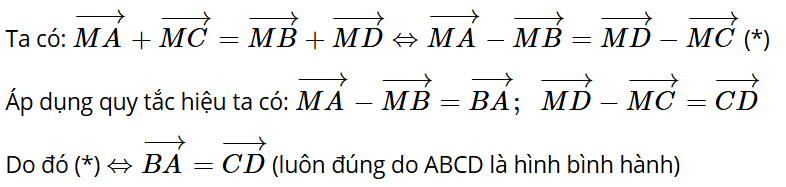
Bài 4.35: Trong mặt phẳng tọa độ Oxy, cho A(2;1), B(-2;5) và C(-5;2).

a) Tìm tọa độ của các vecto $\overrightarrow{BA}$ và $\overrightarrow{BC}.$

b) Chứng minh rằng A, B, C là ba đỉnh của một tam giác vuông. Tính diện tích và chu vi của tam giác đó.

c) Tìm tọa độ trọng tâm G của tam giác ABC.

d) Tìm tọa độ của điểm D sao cho tứ giác BCAD là một hình bình hành.

Trả lời:

a) Ta có: $\overrightarrow{BA}\left(4;-4\right)$ và $\overrightarrow{BC}\left(-3;-3\right).$

b) Ta có: $\overrightarrow{BA}.\overrightarrow{BC}$ = 4.(–3) + (–4).(–3) = –12 + 12 = 0

⇒ BA ⊥ BC

∆ABC vuông tại B.

Diện tích tam giác vuông ABC là:

$S_{\Delta ABC}=\frac{1}{2}.AB.BC$

$=\frac{1}{2}.\sqrt{4^2+{\left(-4\right)}^2}.\sqrt{{\left(-3\right)}^2+{\left(-3\right)}^2}$

$=\frac{1}{2}.4\sqrt{2}.3\sqrt{2}=12$ (đvdt)

c) Tọa độ trọng tâm G của tam giác ABC là:

$\{\begin{array}{c}{x}_G=\frac{2+\left(-2\right)+\left(-5\right)}{3}=\frac{-5}{3}\\ y_G=\frac{1+5+2}{3}=\frac{8}{3}\end{array}$

$\Rightarrow G\left(\frac{-5}{3};\frac{8}{3}\right)$

Vậy tọa độ trọng tâm của tam giác ABC là: $G\left(\frac{-5}{3};\frac{8}{3}\right).$

d) Để tứ giác BCAD là hình bình hành khi $\overrightarrow{DA}=\overrightarrow{BC}$

Ta có: $\overrightarrow{DA}\left(2-x;1-y\right)$ và $\overrightarrow{BC}\left(-3;-3\right)$

Khi đó, ta có hệ phương trình:

$\{\begin{array}{c}2-x=-3\\ 1-y=-3\end{array}\iff \{\begin{array}{c}x=5\\ y=4\end{array}\Rightarrow D\left(5;4\right)$.

Vậy với D(5;4) thì tứ giác BCAD là một hình bình hành.

Bài 4.36: Trong mặt phẳng tọa độ Oxy, cho A(1;2), B(3;4), C(-1;-2) và D(6;5)

a) Tìm tọa độ của các vecto $\overrightarrow{AB}$ và $\overrightarrow{CD}$.

b) Hãy giải thích tại sao các vecto $\overrightarrow{AB}$ và $\overrightarrow{CD}$ cùng phương.

c) Giả sử E là điểm có tọa độ (a;1). Tìm a để vecto $\overrightarrow{AC}$ và $\overrightarrow{BE}$ cùng phương.

d) Với a tìm được, hãy biểu thị vecto $\overrightarrow{AE}$ theo các vecto $\overrightarrow{AB}$ và $\overrightarrow{AC}$.

Trả lời:

a. AB−→−(2;2) và CD−→−(7;7).

b. Do 27=27 nên AB−→− và CD−→− cùng phương.

c. AC−→−(−2;−4), BE−→−(a−3;−3)

Để AC−→− và BE−→− cùng phương thì a−3−2=−3−4

=> a=32

d. AE−→−(12;−1)

Đặt AE−→−=xAB−→−+yAC−→−, với x và y là các số thực.

=> (32;1)=x.(2;2)+y(−2;−4)

⇔{32=2x−2y1=2x−4y

=> x=1,y=14

Vậy AE−→−=AB−→−+14AC−→−

Bài 4.37: Cho vecto $\overrightarrow{a}\ne \overrightarrow{0}.$ Chứng minh rằng $\frac{1}{\left|}.\overrightarrow{a}$ (hay còn được viết là $\frac{\overrightarrow{a}}{\left|}$) là một vecto đơn vị cùng hướng với $\overrightarrow{a}$.

Trả lời:

Bài 4.38: Cho ba vecto $\overrightarrow{a},\overrightarrow{b},\overrightarrow{u}$ với $\left|\overrightarrow{a}\right|=\left|\overrightarrow{b}\right|=1$ và $\overrightarrow{a}\perp \overrightarrow{b}$. Xét một hệ trục Oxy với hệ vecto đơn vị $\overrightarrow{i}=\overrightarrow{a},\overrightarrow{j}=\overrightarrow{b}$. Chứng minh rằng:

a) Vecto $\overrightarrow{u}$ có tọa độ là $\left(\overrightarrow{u}.\overrightarrow{a},\overrightarrow{u}.\overrightarrow{b}\right).$  

b) $\overrightarrow{u}=\left(\overrightarrow{u}.\overrightarrow{a}\right).\overrightarrow{a}+\left(\overrightarrow{u}.\overrightarrow{b}\right).\overrightarrow{b}.$

Trả lời:

a.

Dựng hệ trục tọa độ Oxy với các vecto đơn vị i→=a→,j→=b→ như hình vẽ.

Gọi u→ = OM−→− => u→ có tọa độ bằng tọa độ vecto OM−→−, hay u→(xM;yM)

Ta có: u→.a→=|u→|.|a→|.cos(xOM)=OM.1.cos(xOM)=xM

u→.b→=|u→|.|b→|.cos(yOM)=OM.1.cos(yOM)=yM

Suy ra: Vecto u→ có tọa độ là (u→.a→;u→.b→).

b. Theo a ta có: u→.a→=xM và u→.b→=yM

=> (u→.a→)a→+(u→.b→)b→=xM.a→+yM.b→

Mà a→,b→ là hai vecto đơn vị của hệ trục nên ta có: u→=xM.a→+yM.b→

Vậy u→=(u→.a→)a→+(u→.b→)b→

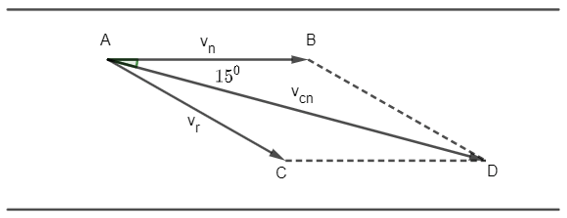
Bài 4.39: Trên sông, một ca nô chuyển động thẳng đều theo hướng S150E với vận tốc có độ lớn bằng 20km/h. Tính vận tốc riêng của ca nô, biết rằng, nước trên sông chảy về hướng đông với vận tốc có độ lớn bằng 3km/h.

Trả lời:

Ta có hình vẽ sau:

Trong đó:

$\overrightarrow{AB}$ là hướng đông

$\overrightarrow{AD}$ là hướng S150E

$\overrightarrow{v_n}$ là vận tốc dòng nước

$\overrightarrow{v_{cn}}$ là vận tốc ca nô

$\overrightarrow{v_r}$ là vận tốc riêng của ca nô

Xét tam giác ABD, có:

$B{D}^2=A{B}^2+A{D}^2-2.AB.AD.cos\widehat{BAD}$ (định lí cosin)

$\iff {\overrightarrow{v_r}}^2={\overrightarrow{v_n}}^2+{\overrightarrow{v_{cn}}}^2-2.\left|\overrightarrow{v_n}\right|.\left|\overrightarrow{v_{cn}}\right|.cos{15}^0$

= 32 + 202 – 2.3.20.cos150

≈ 291,09

⇒ vr ≈ 17,12

Vậy vận tốc riêng của ca nô là 17,12 km/h.