1. Ước chung và ước chung lớn nhất
Hoạt động 1: Tìm các tập hợp Ư(24) và Ư(28).
Lời giải:
+) Vì 24 chia hết cho các số: 1; 2; 3; 4; 6; 8; 12; 24
Do đó: Ư(24) = {1; 2; 3; 4; 6; 8; 12; 24}.
+) Vì 28 chia hết cho các số: 1; 2; 4; 7; 14; 28
Do đó: Ư(28) = {1; 2; 4; 7; 14; 28}.
Hoạt động 2: Gọi ƯC(24, 28) là tập hợp các số vừa là ước của 24, vừa là ước của 28. Hãy viết tập hợp ƯC(24, 28).
Lời giải:
ƯC(24; 28) = {1; 2; 4}
Hoạt động 3: Tìm số lớn nhất trong tập ƯC(24, 28).
Lời giải:
- Số lớn nhất trong ƯC(24; 28) là 4
Câu hỏi 1: Tìm ƯCLN(90, 10).
Lời giải:
Vì 90 ⁝ 10 nên ta có ƯCLN(90, 10) = 10.
Luyện tập 1: Bố có 12 quả bóng màu xanh và 15 quả bóng màu đỏ. Bố muốn chia số bóng cho ba anh em Việt, Hà và Nam đều như nhau gồm cả bóng màu xanh và bóng màu đỏ. Hỏi bố có thực hiện được điều đó hay không?
Lời giải:
Ta có: 3
Nên 3
Do đó bố có thể thực hiện phép chia này.
Vận dụng 1: Tuần này lớp 6A và 6B gồm 40 học sinh nữ và 36 học sinh nam được phân công đi thu gom rác làm sạch bờ biển ở địa phương. Nếu chia nhóm sao cho số học sinh nam và nữ trong các nhóm bằng nhau thì:
a) Có thể chia được thành bao nhiêu nhóm học sinh?
b) Có thể chia nhiều nhất bao nhiêu nhóm học sinh?
Lời giải:
a) Gọi x là số nhóm học sinh chia được (x ∈ N∗)
Khi đó x ∈ ƯC(36, 40)
Ư(36) = {1; 2; 3; 4; 6; 9; 12; 18; 36}
Ư(40) = {1; 2; 4; 5; 8; 10; 20; 40}
=> x ∈ {1; 2; 4}
Vậy có thể chia được thành 1; 2 hoặc 4 nhóm học sinh
b) Số nhóm chia được nhiều nhất là ƯCLN(36, 40) = 4.
2. Cách tìm ước chung lớn nhất
Câu hỏi 2: Tìm ƯCLN(45, 150) biết 45 = 32.5 và 150 = 2.3.52 .
Lời giải:
+) Phân tích các số 45, 150 ra thừa số nguyên tố:
45 = 32.5
150 = 2.3.52
+) Các thừa số nguyên tố chung là: 3; 5
+) Số mũ nhỏ nhất của 3 là 1 và số mũ nhỏ nhất của 5 là 1 nên
ƯCLN(45, 150) = 3. 5 = 15
Vậy ƯCLN(45, 150) = 3. 5 = 15.
Luyện tập 2: Tìm ƯCLN(36, 84).
Lời giải:
36 =
84 =
Ta thấy 2 và 3 là các thừa số nguyên tố chung của 36 và 84. Số mũ nhỏ nhất của 2 là 2, số mũ nhỏ nhất của 3 là 1 nên
ƯCLN(36; 84) =
Vận dụng 2: Một đại hội bộ binh có ba trung đội: trung đội I có 24 chiến sĩ, trung đội II có 28 chiến sĩ, trung đội III có 36 chiến sĩ. Trong cuộc diễu binh, cả ba trung đội phải xếp thành các hàng dọc đều nhau mà không có chiến sĩ nào trong mỗi trung đội bị lẻ hàng. Hỏi có thể xếp được nhiều nhất bao nhiêu hàng dọc?
Lời giải:
Câu hỏi 3: Biết ƯCLN(75; 105) = 15, hãy tìm ƯC(75, 105).
Lời giải:
Vì ƯCLN(75; 105) = 15 nên ƯC(75, 105) = Ư(15) = {1; 3; 5; 15}
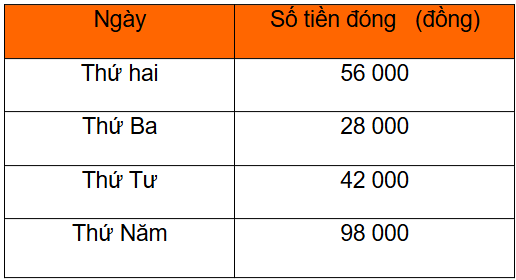
Thử thách nhỏ: Vào ngày thứ Bảy, cô Lan tổ chức cho học sinh đi tham quan Bảo tàng Dân tộc học. Các học sinh đóng tiền mua vé, mỗi em một vé. Số tiền cô Lan thu được từng ngày được ghi lại ở bảng bên.
a) Hỏi số tiền để mua một vé (giá vé được tính theo đơn vị nghìn đồng) có thể là bao nhiêu, biết giá vé lớn hơn 2000 đồng?
b) Có bao nhiêu học sinh tham gia chuyến đi, biết số học sinh trong lớp khoảng từ 20 đến 40 người.
Lời giải:
a) Vì mỗi em mua một vé nên giá vé tính theo nghìn đồng chính là
ƯC(56 000; 28 000; 42 000; 98 000)
Ta có: 56 000 = 26.53.7
28 000 = 25.53.7
42 000 = 24.3.53.7
98 000 = 24.53.72
Ta thấy 2; 5 và 7 là các thừa số nguyên tố chung của 56 000; 28 000; 42 000; 98 000. Số mũ nhỏ nhất của 2 là 4, số mũ nhỏ nhất của 5 là 3, số mũ nhỏ nhất của 7 là 1 nên
ƯCLN (56 000; 28 000; 42 000; 98 000) = 24.53.7 = 14 000
ƯC(56 000; 28 000; 42 000; 98 000) = Ư(14 000)
Do giá vé tính theo đơn vị nghìn đồng nên giá vé chỉ có thể là: 1 000; 2 000; 7 000 đồng.
Mà giá vé lớn hơn 2000 đồng nên giá vé là 7 000 đồng.
b) Tổng số tiền cô Lan thu được thừ thứ Hai đến thứ Năm là:
56 000 + 28 000 + 42 000 + 98 000 = 224 000 (đồng)
Số học sinh tham gia chuyến đi là:
224 000 : 7 000 = 32 (học sinh)
Vậy giá vé là 7 000 đồng và có 32 học sinh tham gia chuyến đi.
3. Rút gọn về phân số tối giản
Câu hỏi 4: Phân số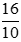 
đã là phân số tối giản chưa? Nếu chưa, hãy rút gọn về phân số tối giản.
Lời giải:
Ta có: 16 = 24 ; 10 = 2.5
+) Thừa số nguyên tố chung là: 2 với số mũ nhỏ nhất là 2 nên ƯCLN(16, 10) = 2
Do đó phân số 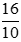chưa là phân số tối giản nên:
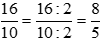. Ta có 
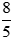là phân số tối giản vì ƯCLN(8, 5) = 1.
Luyện tập 3: Rút gọn về phân số tối giản: a)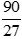 
b) 
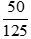
Lời giải:
a)
b)
Bài tập
Bài 2.30: Tìm tập hợp ước chung của:
a) 30 và 45;
b) 42 và 70.
Lời giải:
a) Phân tích các số 30 và 45 ra thừa số nguyên tố:
30 = 2.3.5; 45 = 32.5
+) Ta chọn ra các thừa số nguyên tố chung là: 3 và 5.
+) Số mũ nhỏ nhất của 3 là 1, số mũ nhỏ nhất của 5 là 1. Khi đó:
ƯCLN(30, 45) = 3.5 = 15. Ta được ƯC(30; 45) = Ư(15) = {1; 3; 5; 15}
Vậy ƯC(30; 45) = {1; 3; 5; 15}.
b) Phân tích các số 42 và 70 ra thừa số nguyên tố:
42 = 2.3.7; 70 = 2.5.7;
+) Ta chọn ra các thừa số nguyên tố chung là: 2 và 7.
+) Số mũ nhỏ nhất của 2 là 1, số mũ nhỏ nhất của 7 là 1. Khi đó:
ƯCLN(42, 70) = 2.7 = 14. Ta được ƯC(42; 70) = Ư(14) = {1; 2; 7; 14}
Vậy ƯC(42; 70) = {1; 2; 7; 14}.
Bài 2.31: Tìm ƯCLN của hai số:
a) 40 và 70;
b) 55 và 77.
Lời giải:
a) Ta có: 40 = 23.5; 70 = 2.5.7
Vậy ƯCLN(40, 70) = 2.5 = 10
b) Ta có: 55 = 5.11; 77 = 7.11
Vậy ƯCLN(55, 77) = 11.
Bài 2.32: Tìm ƯCLN của:
a) 22.5 và 2. 3. 5;
b) 24.3; 22.32.5 và 24.11
Lời giải:
a)
Ta thấy 2 và 5 là thừa số nguyên tố chung. Số mũ nhỏ nhất của 2 là 1 và số mũ nhỏ nhất của 5 là 1 nên
ƯCLN cần tìm là 2.5 = 10
b)
Ta thấy 2 là thừa số nguyên tố chung. Số mũ nhỏ nhất của 2 là
ƯCLN cần tìm là
Bài 2.33: Cho hai số a = 72 và b = 96
a) Phân tích a và b ra thừa số nguyên tố;
b) Tìm ƯCLN(a, b), rồi tìm ƯC(a, b).
Lời giải:
a) Phân tích a và b ra thừa số nguyên tố
Ta có:
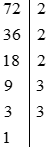
Do đó: a = 72 = 23.32.
Lại có:
Vậy b = 96 = 25.3.
b) Ta thấy 2 và 3 là các thừa số chung của 70 và 96. Số mũ nhỏ nhất của 2 là 3 và số mũ nhỏ nhất của 3 là 1 nên
ƯCLN(72; 96) = 23 . 3 = 24
ƯC(a, b) = Ư(24) = {1; 2; 3; 4; 6; 8; 12; 24}.
Bài 2.34: Các phân số sau đã là phân số tối giản chưa? Nếu chưa, hãy rút gọn về phân số tối giản?
a)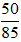 
; b)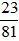 
.
Lời giải:
a)
Ta có ƯCLN(50; 85) = 45 nên
Ta có:
Ta được
b)
Ta có ƯCLN(23; 81) = 1 nên
Bài 2.35: Hãy cho hai ví dụ về hai số có ƯCLN bằng 1 mà cả hai đều là hợp số.
Lời giải:
Hai ví dụ về hai số có ƯCLN bằng 1 mà cả hai đều là hợp số:
4 và 9 là hai hợp số nhưng ƯCLN của 4 và 9 là 1;
8 và 27 là hai hợp số nhưng ƯCLN của 8 và 27 là 1.
Chú ý: Ta có thể lấy các ví dụ khác