Giải SGK Toán 6 Kết nối tri thức Bài 12: Bội chung - Bội chung nhỏ nhất

1. Bội chung và bội chung nhỏ nhất

Hoạt động 1: Tìm các tập hợp B(6), B(9).

Lời giải:

B(6) = {0; 6; 12; 18; 24; 30; 36; 42, 48; 54, ...}

B(9) = {0; 9; 18; 27; 36; 45; 54; 63, ...}

Hoạt động 2: Gọi BC(6, 9) là tập hợp các số vừa là bội của 6, vừa là bội của 9. Hãy viết tập BC(6, 9).

Lời giải:

BC(6; 9) = {0; 18; 36; 54, ...}

Hoạt động 3: Tìm số nhỏ nhất khác 0 trong tập BC(6; 9).

Lời giải:

Ta có: BC(6; 9) = {0; 18; 36; 54, ...}

Số nhỏ nhất khác 0 trong tập BC(6; 9) là 18.

Câu hỏi 1: Tìm BCNN(36, 9).

Lời giải:

Vì 36 ⁝ 9 nên BCNN(36, 9) = 36.

Luyện tập 1: Tìm bội chung nhỏ nhất của:

a) 6 và 8;

b) 8; 9; 72.

Lời giải:

a) B(6) = {0; 6; 12; 18; 24; 30; 36; 42; 48; ...}

    B(8) = {0; 8; 16; 24; 32; 40; 48; ...}

Do đó BC(6; 8) = {0; 24; 48; ...}

Vậy BCNN(6; 8) = 24

b) Vì 8.9 = 72 ; và ƯCLN(8; 9) = 1 nên BCNN(8; 9; 72) = 72

Vận dụng: Có hai chiếc máy A và B. Lịch bảo dưỡng định kì đối với máy A là 6 tháng và đối với máy B là 9 tháng. Hai máy vừa cùng được bảo dưỡng vào tháng 5. Hỏi sau ít nhất bao nhiêu tháng nữa thì hai máy lại được bảo dưỡng trong cùng một tháng?

Lời giải:

Số tháng cần tìm là BCNN(6, 9)

B(6) = {0; 6; 12; 18; 24; 30; 36; 42; 48; 54; ...}

B(9) = {0; 9; 18; 27; 36; 45; 54; 63; ...}

Nên BC(6, 9) = {0; 18; 36; 54; ...}

Do đó BCNN(6, 9) = 18

Vậy sau ít nhất 18 tháng nữa thì hai máy được bảo dưỡng cùng một tháng.

2. Cách tìm bội chung nhỏ nhất

Câu hỏi 2: Tìm bội chung nhỏ nhất của 9 và 15, biết: 9 = 32 và 15 = 3.5.

Lời giải:

Ta có: 9 = 32;                            15 = 3.5.

+) Thừa số nguyên tố chung là 3 và riêng là 5.

+) Số mũ lớn nhất của 3 là 2, số mũ lớn nhất của 5 là 1

Khi đó BCNN(9, 15) =32. 5 = 45.

Câu hỏi 3: Biết bội chung nhỏ nhất của 8 và 6 là 24. Tìm các bội chung nhỏ hơn 100 của 8 và 6.

Lời giải:

BC(8, 6) = B(24) ={0; 24; 48; 72; 96; 120;...}

Vậy các bội chung nhỏ hơn 100 của 8 và 6 là : 0; 24; 48; 72; 96

Luyện tập 2: Tìm bội chung nhỏ nhất của 15 và 54. Từ đó, hãy tìm các bội chung nhỏ hơn 1 000 của 15 và 54.

Lời giải:

Phân tích 15 và 54 ra thừa số nguyên tố:  15 = 3.5  ;  54 = 2.33

Ta thấy thừa số nguyên tố chung là 3 và thừa số nguyên tố riêng là 2 và 5

Vậy BCNN(15; 54) = 2.33.5=270

Do đó BC(15; 54) = {0; 270; 540; 810; 1080; ...} nên bội chung nhỏ hơn 1000 của 15 và 54 là 0; 270; 540; 810

Thử thách nhỏ: Lịch xuất bến của một số xe buýt tại bến xe Mỹ Đình (Hà Nội) được ghi ở bảng bên. Giả sử các xe buýt xuất bến cùng lúc vào 10 giờ 35 phút. Hỏi vào các thời điểm nào trong ngày (từ 10 giờ 35 phút đến 22 giờ) các xe buýt này lại xuất bến cùng một lúc?

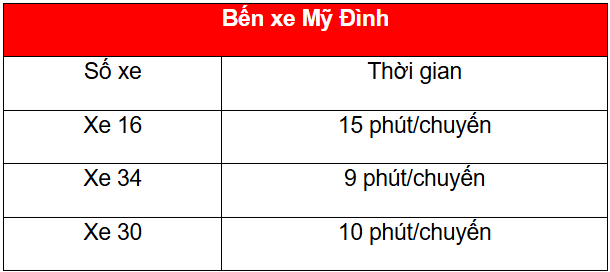
Lời giải:

Ta có: 9 = 32 ;       10 = 2. 5         15 = 3.5.

Thừa số nguyên tố chung là 3 và riêng là 2 và 5.

Số mũ lớn nhất của 3 là 1, số mũ lớn nhất của 3 là 2, số mũ lớn nhất của 5 là 1

Khi đó BCNN(9, 10, 15) = 2.32. 5 = 90.

Do đó cứ sau 90 phút thì ba xe lại xuất bến cùng một lúc.

Đổi 90 phút = 1 giờ 30 phút

Từ 10 giờ 35 phút thì sau 10 giờ 35 phút + 1 giờ 30 phút = 12 giờ 05 phút các xe xuất bến cùng một lúc

Tương tự như vậy thì 10 giờ 35 phút đến 22 giờ các xe xuất bến cùng một lúc vào các giờ: 12 giờ 05 phút; 13 giờ 35 phút; 15 giờ 05 phút; 16 giờ 35 phút; 18 giờ 05 phút; 

19 giờ 35 phút; 21 giờ 05 phút.

3. Quy đồng mẫu các phân số

Câu hỏi 3: Quy đồng mẫu hai phân số: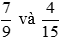 

Lời giải:

Ta có: 9 = 32;    15 = 3. 5 nên BCNN(9, 15) = 32.5 = 45.

Ta có thể lấy mẫu chung của hai phân số trên là 45. Do đó:

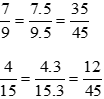
Luyện tập 3:

(1) Quy đồng mẫu các phân số sau: a)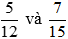                 b)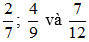 

(2) Thực hiện các phép tính sau:        a)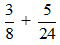                 b)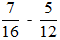 

Lời giải:

1. a) Ta có BCNN(12; 15) = 60 nên ta lấy mẫu chung của hai phân số là 60. 

512=5.512.5=2560

715=7.415.4=2860

b) Ta có BCNN(7; 9; 12) = 252 nên ta lấy mẫu chung của ba phân số là 252. 

27=2.367.36=72252

49=4.289.28=112252

712=7.2112.21=147252

2) a) Ta có BCNN(8; 24) = 24 nên:

38+524=3.38.3+524=924+524=1424=712

b) Ta có BCNN(12; 16) = 48 nên:

716−512=7.316.3−5.412.4=2148−2048=148

Bài tập

Bài 2.36: Tìm bội chung nhỏ hơn 200 của

a) 5 và 7;

b) 3, 4 và 10.

Lời giải:

a) Do 5 và 7 là hai số nguyên tố cùng nhau nên:

BCNN(5, 7) = 5.7 = 35 => BC(5, 7) = B(35) = {0; 35; 70; 105; 140; 175; 210; ...}

Vậy bội chung nhỏ hơn 200 của 5 và 7 là 0; 35; 70; 105; 140; 175.

b) Ta có: 3 = 3; 4 = 22; 10 = 2.5

Không có thừa số nguyên tố chung ; thừa số nguyên tố riêng là 2,3,5. Số mũ lớn nhất của 2;3;5 lần lượt là 2;1;1 nên BCNN(3, 4, 10) = 22.3.5 = 60

=> BC(3, 4, 10) = B(60) = {0; 60; 120; 180; 240; ...}

Vậy bội chung nhỏ hơn 200 của 3, 4 và 10 là 0; 60; 120; 180.

Bài 2.37: Tìm BCNN của:

a) 2.33 và 3.5

b) 2.5.72 và 3.52.7

Lời giải:

a) 2.33 và 3.5

+) Ta thấy các thừa số nguyên tố chung là 3 và thừa số nguyên tố riêng là 1 và 5

+) Số mũ lớn nhất của 2 là 1, số mũ lớn nhất của 3 là 3, số mũ lớn nhất của 5 là 1

Vậy BCNN cần tìm là 2.33.5 = 270.

b) 2.5.72   và 3.52.7        

+) Ta thấy các thừa số nguyên tố chung là 5 và 7; thừa số nguyên tố riêng là 2 và 3

+) Số mũ lớn nhất của 2 là 1, số mũ lớn nhất của 3 là 1, số mũ lớn nhất của 5 là 2, số mũ lớn nhất của 7 là 2

Vậy BCNN cần tìm là 2.3.52.72 = 7 350.

Bài 2.38: Tìm BCNN của các số sau:

a) 30 và 45;

b) 18, 27 và 45.

Lời giải:

a) 30 và 45

30 = 2.3.5  ;  45 = 32.5

Ta thấy thừa số nguyên tố chung là 3 và 5; thừa số nguyên tố riêng là 2

Vậy BCNN(30; 45) = 2.32.5=90

b) 18, 27 và 45

18 = 2.32  ;  27 = 33  ;  45 = 32.5

Ta thấy thừa số nguyên tố chung là 3; thừa số nguyên tố riêng là 2 và 5

Vậy BCNN(30; 45) = 2.33.5=270

Bài 2.39: Tìm số tự nhiên a nhỏ nhất khác 0 biết rằng a ⋮ 28 và a ⋮ 32

Lời giải:

Số tự nhiên a nhỏ nhất khác 0 và a ⋮ 28 và a ⋮ 32 

Do đó a = BCNN(28, 32)

28 = 2².7

32 = 2⁵

Thừa số nguyên tố chung là 2, thừa số nguyên tố riêng là 7. Số mũ lớn nhất của 2 là 5, của 7 là 1

Nên a = BCNN(28, 32) = 2⁵.7 = 224.

Bài 2.40: Học sinh lớp 6A khi xếp thành 3 hàng, 4 hàng hay 9 hàng đều vừa đủ. Biết số học sinh của lớp từ 30 đến 40. Tính số học sinh của lớp 6A

Lời giải:

Học sinh lớp 6A khi xếp thành 3 hàng, 4 hàng hay 9 hàng đều vừa đủ.

Nên số học sinh của lớp 6A là BC(3; 4; 9) 

Ta có: 3 = 3;  4 = 22;   9 = 32

Ta thấy thừa số nguyên tố riêng là 2 và 3, không có thừa số nguyên tố chung

Số mũ lớn nhất của 2 là 2, số mũ lớn nhất của 3 là 2

Khi đó: BCNN(3; 4; 9) = 22.32 = 36

Do đó BC(3; 4; 9) = B(36) = {0; 36; 72; ...}

Mà số học sinh lớp 6A từ 30 đến 40 nên số học sinh lớp 6A là 36.

Vậy số học sinh lớp 6A là 36 học sinh.

Bài 2.41: Hai đội công nhân trồng được một số cây như nhau. Mỗi công nhân đội I đã trồng 8 cây, mỗi công nhân đội II đã trồng 11 cây. Tính số cây mỗi đội đã trồng, biết rằng số cây đó trong khoảng từ 100 đến 200 cây.

Lời giải:

Vì số cây hai đội trồng được như nhau mà mỗi công nhân đội I đã trồng 8 cây, mỗi công nhân đội II đã trồng 11 cây.

Nên số cây mỗi đội trồng được là BC(8; 11)

BCNN(8; 11) = 88

Do đó số cây mỗi đội trồng là BC(8; 11) = {0; 88; 176; 264; ...}

Mà số cây trong khoảng từ 100 đến 200 nên số cây mỗi đội trồng được là 176 cây.

Bài 2.42: Cứ 2 ngày, Hà đi dạo cùng bạn cún đáng yêu của mình. Cứ 7 ngày, Hà lại tắm cho cún. Hôm nay, cún vừa được đi dạo, vừa được tắm. Hỏi sau ít nhất bao nhiêu ngày nữa thì cún vừa được đi dạo, vừa được tắm?

Lời giải:

Số ngày ít nhất mà cún vừa được đi dạo, vừa được tắm là BCNN (2, 7)

Mà 2 và 7 là hai số nguyên tố cùng nhau nên BCNN (2, 7) = 2.7 = 14

Vậy số ít nhất mà cún vừa được đi dạo, vừa được tắm là 14 ngày.

Bài 2.43: Quy đồng mẫu các phân số sau:

a)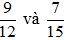 

b)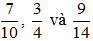 

Lời giải:

a) Ta có: 12.22.3; nên BCNN(12, 15) = 22.3.5 = 60. Do đó ta có thể chọn mẫu chung là 60.

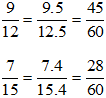
b) Ta có: 10 = 2.5; 4 = 22; 14 = 2. 7 nên BCNN(10, 4, 14) = 22.5.7 = 140. Do đó ta có thể chọn mẫu chung là 140

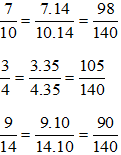
Bài 2.44: Thực hiện các phép tính sau:

a)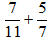

b)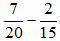

Lời giải:

a) BCNN(11; 7) = 77 nên chọn mẫu chung là 77

  711 + 57

= 7.711.7+5.117.11=4977+5577=10477

b) BCNN(20; 15)= 60 nên chọn mẫu chung là 60

  720−215

= 7.320.3−2.415.4=2160−860=1360