Giải SGK Toán 9 Cánh Diều Bài 2: Bất phương trình bậc nhất một ẩn

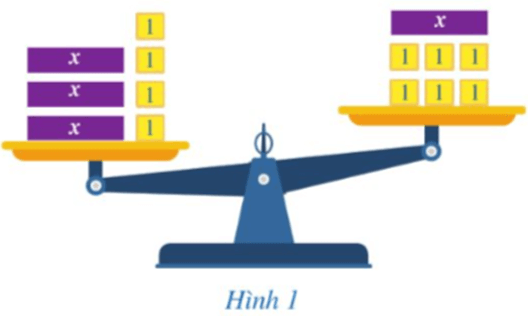
Khởi động: Giả sử mỗi hộp màu tím đặt trên đĩa cân ở Hình 1 đều có khối lượng là x kg, còn mỗi hộp màu vàng đều có khối lượng là 1 kg. Khi đó, hai biểu thức biểu thị (theo x) tổng khối lượng của các hộp xếp ở đĩa cân bên trái, đĩa cân bên phải lần lượt là 3x + 4, x + 6. Do đĩa cân lệch về bên trái nên ta có hệ thức: 3x + 4 > x + 6.

Trong toán học, hệ thức 3x + 4 > x + 6 được gọi là gì?

Trả lời:

- Trong toán học, hệ thức 3x + 4 > x + 6 được gọi là một bất phương trình ẩn x.

I. Mở đầu về bất phương trình một ẩn

Hoạt động 1: Xét hệ thức 3x + 4 > x + 6 (1) nêu trong bài toán ở phần mở đầu.

a) Các biểu thức 3x + 4, x + 6 có phải là hai biểu thức của cùng một biến x hay không?

b) Khi thay giá trị x = 5 vào hệ thức (1), ta có được một khẳng định đúng hay không?

Trả lời:

Luyện tập, vận dụng 1: Cho biết giá trị x = 3 là nghiệm của bất phương trình nào trong các bất phương trình sau:

a) 5x + 4 > 4x – 12;

b) x2 – 3x + 5 ≤ 4.

Trả lời:

a) Khi thay x = 3 vào bất phương trình đã cho, ta được:

5.3 + 4 > 4.3 – 12 hay 19 > 0 là khẳng định đúng.

Vậy x = 3 là nghiệm của bất phương trình đã cho.

b) Khi thay x = 3 vào bất phương trình đã cho, ta được:

32 – 3.3 + 5 ≤ 4 hay 5 ≤ 4 là khẳng định không đúng.

Vậy x = 3 là không nghiệm của bất phương trình đã cho.

II. Bất phương trình bậc nhất một ẩn

Hoạt động 2: Cho bất phương trình (ẩn x): 5x + 20 > 0.

Đa thức ở vế trái của bất phương trình đó có bậc bằng bao nhiêu?

Trả lời:

- Đa thức ở vế trái của phương trình đó có bậc bằng 1.

Luyện tập, vận dụng 2: Nêu hai ví dụ về bất phương trình bậc nhất ẩn x.

Trả lời:

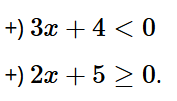
Luyện tập, vận dụng 3: Kiểm tra xem x = –7 có phải là nghiệm của bất phương trình bậc nhất 2x + 15 ≥ 0 hay không?

Trả lời:

a) Thay x = –7 vào bất phương trình đã cho, ta được:

2.(–7) + 15 ≥ 0 hay 1 ≥ 0 là khẳng định đúng.

Vậy x = –7 là nghiệm của bất phương trình bậc nhất 2x + 15 ≥ 0.

Hoạt động 3: Giải bất phương trình: 4x – 32 < 0 (2)

Trả lời:

Để giải bất phương trình (2), ta làm như sau:

4x – 32 < 0

Cộng cả hai vế với 32

4x < 32

Nhân cả hai vế với 

x < 8.

Vậy nghiệm của bất phương trình (2) là x < 8.

Luyện tập, vận dụng 4: Giải các bất phương trình:

a) –8x – 27 < 0;

b) $\frac{5}{4}$x + 20$\ge$0.

Trả lời:

Hoạt động 4: Giải bất phương trình: 3x + 4 > x + 12.

Trả lời:

Để giải bất phương trình trên, ta làm như sau:

3x + 4 > x + 12

3x + 4 – x > 12 ← Cộng cả hai vế với –x

2x > 12 – 4 ← Cộng cả hai vế với –4

2x > 8

x > 4. ← Nhân cả hai vế với $\frac{1}{2}$.

Vậy nghiệm của bất phương trình đã cho là x > 4.

Luyện tập, vận dụng 5: Giải bất phương trình: 2(x – 0,5) – 1,4 ≥ 1,5 – (x + 1,2).

Trả lời:

2(x – 0,5) – 1,4  1,5 – (x + 1,2) 

Vậy nghiệm của bất phương trình đã cho là 

Bài tập

Bài tập 1: Kiểm tra xem số nào là nghiệm của mỗi bất phương trình tương ứng sau đây.

a) x2 – 3x + 2 > 0 với x = –3; x = 1,5.

b) 2 – 2x < 3x + 1 với x = $\frac{2}{5}$; x = $\frac{1}{5}$

Trả lời:

a) ⦁ Thay x = –3 vào bất phương trình đã cho, ta được:

(–3)2 – 3.(–3) + 2 > 0 hay 20 > 0 là khẳng định đúng.

Do đó x = –3 là nghiệm của bất phương trình đã cho.

⦁ Thay x = 1,5 vào bất phương trình đã cho, ta được:

1,52 – 3.1,5 + 2 > 0 hay –0,25 > 0 là khẳng định không đúng.

Do đó x = 1,5 không là nghiệm của bất phương trình đã cho.

b) ⦁ Thay x = $\frac{2}{5}$ vào bất phương trình đã cho, ta được:

2 - 2.$\frac{2}{5}$ < 3.$\frac{2}{5}$+1 hay $\frac{6}{5}$<$\frac{11}{5}$ là khẳng định đúng.

Do đó x = $\frac{2}{5}$ là nghiệm của bất phương trình đã cho.

⦁ Thay x = $\frac{1}{5}$ vào bất phương trình đã cho, ta được:

2-2.$\frac{1}{5}$ < 3.$\frac{1}{5}$+1 hay $\frac{8}{5}<\frac{8}{5}$ là khẳng định không đúng.

Do đó x = $\frac{1}{5}$ không là nghiệm của bất phương trình đã cho.

Bài tập 2: Giải các bất phương trình:

a) 2x + 6 > 1;

b) 0,6x + 2 > 6x + 9;

c) 1,7x + 4 ≥ 2 + 1,5x.

Trả lời:

a) 2x + 6 > 1

2x > – 5

Vậy nghiệm của bất phương trình đã cho là  

b) 

Vậy nghiệm của bất phương trình đã cho là 

c) 1,7x + 

Vậy nghiệm của bất phương trình đã cho là 

Bài tập 3: Giải các bất phương trình:

a) $\frac{8-3x}{2}$ - x < 5;

b) 3 - 2x - $\frac{6+4x}{3}$>0;

c) 0,7x+$\frac{2x-4}{3}-\frac{x}{6}$>1.

Trả lời:

b) 3 - 2x - $\frac{6+4x}{3}$>0

3.3 – 3.2x – (6 + 4x) > 0

9 – 6x – 6 – 4x > 0

–10x > –9 + 6

–10x > –3

x < $\frac{3}{10}$.

Vậy nghiệm của bất phương trình đã cho là x < $\frac{3}{10}$.

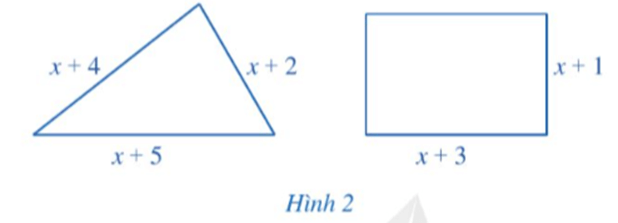
Bài tập 4: Tìm số thực dương x sao cho ở Hình 2 chu vi của hình tam giác lớn hơn chu vi của hình chữ nhật:

Trả lời:

Chu vi của hình tam giác là: (x + 4) + (x + 2) + (x + 5) = 3x + 11.

Chu vi của hình chữ nhật là: 2.(x + 1 + x + 3) = 2.(2x + 4) = 4x + 8.

Theo bài, chu vi hình tam giác lớn hơn chu vi của hình chữ nhật nên ta có bất phương trình: 3x + 11 > 4x + 8.

Giải bất phương trình:

3x + 11 > 4x + 8

3x – 4x > 8 – 11

–x > –3

x < 3.

Mà x là số thực dương nên x > 0.

Vậy 0 < x < 3.

Bài tập 5: Một kho chứa 100 tấn xi măng, mỗi ngày đều xuất đi 20 tấn xi măng. Gọi x là số ngày xuất xi măng của kho đó. Tìm x sao cho sau x ngày xuất hàng, khối lượng xi măng còn lại trong kho ít nhất là 10 tấn.

Trả lời:

Số xi măng xuất sau x ngày là: 20x (tấn)  (x > 0)

Số xi măng còn lại sau x ngày: 100 – 20x (tấn)

Để khối lượng xi măng còn lại trong kho ít nhất là 10 tấn ta có:

100 – 20x 

Vậy sau 4 ngày xuất hàng, khối lượng xi măng còn lại trong kho còn lại ít nhất là 10 tấn.