Giải SGK Toán 9 Cánh Diều Bài 4: Một số phép biến đổi căn thức bậc hai của biểu thức đại số

Khởi động:

Khí trong động cơ giãn nở từ áp suất p1 và thể tích V1 đến áp suất p2 và thể tích V2 thoả mãn đẳng thức: $\frac{p_1}{p_2}={\left(\frac{V_1}{V_2}\right)}^2.$

(Nguồn: Engineering Problems Illustrating Mathematics, John W. Cell, năm 1943).

Có thể tính được thể tích V1 theo p1, p2 và V2 được hay không?

Trả lời:

Từ công thức $\frac{p_1}{p_2}={\left(\frac{V_1}{V_2}\right)}^2$ ta có thể tính được thể tích V1 theo p1, p2 và V2.

I. Căn thức bậc hai của một bình phương

Hoạt động 1: Tìm số thích hợp cho :

a) $\sqrt{7^2}$ = ;

b) $\sqrt{{(-9)}^2}$ = ;

c) $\sqrt{a^2}$ =  với a là một số cho trước.

Trả lời:

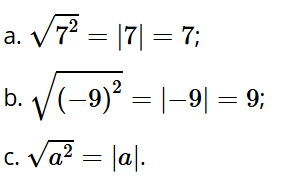
Luyện tập, vận dụng 1: Áp dụng quy tắc về căn thức bậc hai của một bình phương, hãy rút gọn biểu thức:

a) $\sqrt{x^2+6x+9}$ với x < –3;

b) $\sqrt{y^4+2y^2+1}.$

Trả lời:

a)  

b) 

.

II. Căn thức bậc hai của một tích

Hoạt động 2: So sánh:

a) $\sqrt{16\cdot 0,25}$ và $\sqrt{16}\cdot \sqrt{0,25};$

b) $\sqrt{a\cdot b}$ và $\sqrt{a}\cdot \sqrt{b}$ với a, b là hai số không âm.

Trả lời:

a) Áp dụng quy tắc về căn bậc hai của một tích, ta có:

$\sqrt{16\cdot 0,25}=\sqrt{16}\cdot \sqrt{0,25}.$

b) Với a, b là hai số không âm, áp dụng quy tắc về căn bậc hai của một tích, ta có: $\sqrt{a\cdot b}=\sqrt{a}\cdot \sqrt{b}.$

Luyện tập, vận dụng 2: Áp dụng quy tắc về căn thức bậc hai của một tích, hãy rút gọn biểu thức:

a) $\sqrt{9x^4};$

b) $\sqrt{3a^3}\cdot \sqrt{27a}$ với a > 0.

Trả lời:

a)  

b) 

III. Căn thức bậc hai của một thương

Hoạt động 3: So sánh:

a) $\sqrt{\frac{49}{169}}$ và $\frac{\sqrt{49}}{\sqrt{169}};$

b) $\sqrt{\frac{a}{b}}$ và $\frac{\sqrt{a}}{\sqrt{b}}$ với a là số không âm, b là số dương.

Trả lời:

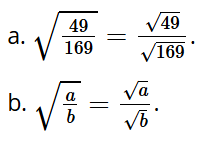
Luyện tập, vận dụng 3: Áp dụng quy tắc về căn thức bậc hai của một thương, hãy rút gọn biểu thức:

a) $\sqrt{\frac{9}{{\left(x-3\right)}^2}}$ với x > 3;

b) $\frac{\sqrt{48x^3}}{\sqrt{3x^5}}$ với x > 0.

Trả lời:

a) 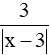$\sqrt{\frac{9}{{\left(x-3\right)}^2}}=\frac{\sqrt{9}}{\sqrt{{\left(x-3\right)}^2}}$ =  = $\frac{3}{x-3}$ (vì x – 3 > 0 khi x > 3).

b) 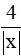$\frac{\sqrt{48x^3}}{\sqrt{3x^5}}=\sqrt{\frac{48x^3}{3x^5}}=\sqrt{\frac{16}{x^2}}=\frac{\sqrt{16}}{\sqrt{x^2}}$ =  = $\frac{4}{x}$ (vì x > 0).

IV. Trục căn thức ở mẫu

Hoạt động 4: Xét phép biến đổi: $\frac{5}{\sqrt{3}}=\frac{5\cdot \sqrt{3}}{{\left(\sqrt{3}\right)}^2}=\frac{5\sqrt{3}}{3}.$ Hãy xác định mẫu thức của mỗi biểu thức sau: $\frac{5}{\sqrt{3}};\frac{5\sqrt{3}}{3}$.

Trả lời:

Mẫu thức của  là .

Mẫu thức của  là 3.

Luyện tập, vận dụng 4: Trục căn thức ở mẫu: $\frac{x^2-1}{\sqrt{x-1}}$ với x > 1.

Trả lời:

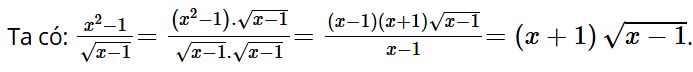
Luyện tập, vận dụng 5: Trục căn thức ở mẫu: $\frac{x-1}{\sqrt{x}-1}$ với x > 1.

Trả lời:

Với x > 1, ta có:

$\frac{x-1}{\sqrt{x}-1}=\frac{\left(x-1\right)\cdot \left(\sqrt{x}+1\right)}{\left(\sqrt{x}-1\right)\cdot \left(\sqrt{x}+1\right)}$

$=\frac{\left(x-1\right)\left(\sqrt{x}+1\right)}{{\left(\sqrt{x}\right)}^2-1^2}=\frac{\left(x-1\right)\left(\sqrt{x}+1\right)}{x-1}=\sqrt{x}+1.$

Luyện tập, vận dụng 6: Trục căn thức ở mẫu: $\frac{1}{\sqrt{x+1}-\sqrt{x}}$ với x ≥ 0.

Trả lời:

Ta có:  

Bài tập

Bài tập 1: Áp dụng quy tắc về căn thức bậc hai của một bình phương, hãy rút gọn biểu thức:

a) $\sqrt{{\left(5-x\right)}^2}$ với x ≥ 5;

b) $\sqrt{{\left(x-3\right)}^4};$

c) $\sqrt{{\left(y+1\right)}^6}$ với y < –1.

Trả lời:

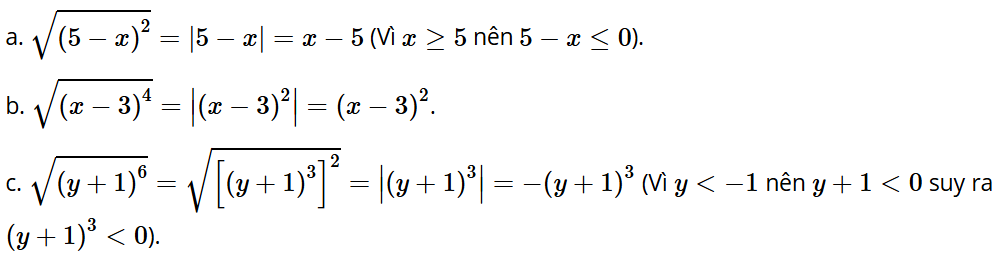
Bài tập 2: Áp dụng quy tắc về căn thức bậc hai của một tích, hãy rút gọn biểu thức:

a) $\sqrt{25{\left(a+1\right)}^2}$ với a > –1;

b) $\sqrt{x^2{\left(x-5\right)}^2}$ với x > 5;

c) $\sqrt{2b}\cdot \sqrt{32b}$ với b > 0;

d) $\sqrt{3c}\cdot \sqrt{27c^3}$ với c > 0.

Trả lời:

a) $\sqrt{25{\left(a+1\right)}^2}=\sqrt{25}\cdot \sqrt{{\left(a+1\right)}^2}$ = 5|a+1| = 5(a+1) (vì a + 1 > 0 khi a > –1).

b) $\sqrt{x^2{\left(x-5\right)}^2}=\sqrt{x^2}\cdot \sqrt{{\left(x-5\right)}^2}$ = |x|.|x-5| = x(x-5) (vì x > 0 và x – 5 > 0 khi x > 5).

c) $\sqrt{2b}\cdot \sqrt{32b}=\sqrt{2b\cdot 32b}=\sqrt{64b^2}=\sqrt{64}\cdot \sqrt{b^2}$ = 8|b|= 8b (vì b > 0).

d) $\sqrt{3c}\cdot \sqrt{27c^3}=\sqrt{3c\cdot 27c^3}=\sqrt{81c^4}=\sqrt{81}\cdot \sqrt{c^4}$ = 9|c2| = 9c2 (vì c2 ≥ 0 với mọi số thực c).

Bài tập 3: Áp dụng quy tắc về căn thức bậc hai của một thương, hãy rút gọn biểu thức:

a) $\sqrt{\frac{{\left(3-a\right)}^2}{9}}$ với a > 3;

b) $\frac{\sqrt{75x^5}}{\sqrt{5x^3}}$ với x > 0;

c) $\sqrt{\frac{9}{x^2-2x+1}}$ với x > 1;

d) $\sqrt{\frac{x^2-4x+4}{x^2+6x+9}}$ với x ≥ 2.

Trả lời:

a) 

b) 

c) 

d) .

Bài tập 4: Trục căn thức ở mẫu:

a) $\frac{9}{2\sqrt{3}};$

b) $\frac{2}{\sqrt{a}}$ với a > 0;

c) $\frac{7}{3-\sqrt{2}};$

d) $\frac{5}{\sqrt{x}+3}$ với x > 0, x ≠ 9;

e) $\frac{\sqrt{3}-\sqrt{2}}{\sqrt{3}+\sqrt{2}};$

g) $\frac{1}{\sqrt{x}-\sqrt{3}}$ với x > 0, x ≠ 3.

Trả lời:

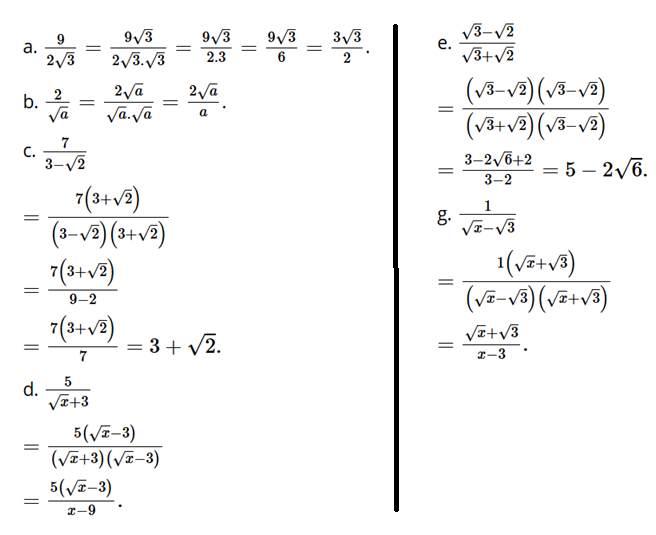
Bài tập 5: Rút gọn biểu thức: $\frac{\sqrt{a}}{\sqrt{a}-\sqrt{b}}-\frac{\sqrt{b}}{\sqrt{a}+\sqrt{b}}-\frac{2b}{a-b}$ với a ≥ 0, b ≥ 0, a ≠ b.

Trả lời:

Với a ≥ 0, b ≥ 0, a ≠ b, ta có:

$\frac{\sqrt{a}}{\sqrt{a}-\sqrt{b}}-\frac{\sqrt{b}}{\sqrt{a}+\sqrt{b}}-\frac{2b}{a-b}$

$=\frac{\sqrt{a}\cdot \left(\sqrt{a}+\sqrt{b}\right)}{\left(\sqrt{a}-\sqrt{b}\right)\cdot \left(\sqrt{a}+\sqrt{b}\right)}-\frac{\sqrt{b}\cdot \left(\sqrt{a}-\sqrt{b}\right)}{\left(\sqrt{a}+\sqrt{b}\right)\cdot \left(\sqrt{a}-\sqrt{b}\right)}-\frac{2b}{a-b}$

$=\frac{{\left(\sqrt{a}\right)}^2+\sqrt{a}\cdot \sqrt{b}}{{\left(\sqrt{a}\right)}^2-{\left(\sqrt{b}\right)}^2}-\frac{\sqrt{a}\cdot \sqrt{b}-{\left(\sqrt{b}\right)}^2}{{\left(\sqrt{a}\right)}^2-{\left(\sqrt{b}\right)}^2}-\frac{2b}{a-b}$

$=\frac{a+\sqrt{ab}}{a-b}-\frac{\sqrt{ab}-b}{a-b}-\frac{2b}{a-b}$

$=\frac{a+\sqrt{ab}-\sqrt{ab}+b-2b}{a-b}$$=\frac{a-b}{a-b}=1.$