Câu hỏi khởi động: Một lạng thịt bò chứa 26 g protein, một lạng thịt cá chứa 22 g protein. Bác An dự định chỉ bổ sung 70 g protein từ thịt bò và thịt cá trong một ngày.

Số lạng thịt bò và số lạng thịt cá mà bác An ăn trong một ngày cần thoả mãn điều kiện ràng buộc gì để đáp ứng nhu cầu bổ sung protein của bác An?
Trả lời:
Gọi x, y lần lượt là số lạng thịt bò, số lạng thịt cá mà bác An ăn trong một ngày. Khi đó:
⦁ số g protein được bổ sung từ x lạng thịt bò là: 26x (g);
⦁ số g protein được bổ sung từ y lạng thịt cá là: 22y (g).
Theo bài, bác An dự định chỉ bổ sung 70 g protein từ thịt bò và thịt cá trong một ngày nên ta có: 26x + 22y = 70.
Vậy hệ thức liên hệ giữa x và y để đáp ứng nhu cầu bổ sung protein của bác An là 26x + 22y = 70.
I. Phương trình bậc nhất hai ẩn
Hoạt động 1: Trong bài toán ở phần mở đầu, ta gọi x, y lần lượt là số lạng thịt bò, số lạng thịt cá mà bác An ăn trong một ngày. Viết hệ thức liên hệ giữa x và y để đáp ứng nhu cẩu bổ sung protein của bác An.
Trả lời:
+ Lượng protein mà x lạng thịt bò bác An ăn trong một ngày cung cấp là: 26 x (g);
+ Lượng protein mà y lạng thịt các bác An ăn trong một ngày cung cấp là: 22y (g);
+ Để đáp ứng nhu cầu bổ sung protein của bác An, x và 𝑦 cần thỏa mãn: 26x + 22y = 70
Hoạt động 2: Cho phương trình bậc nhất hai ẩn x, y:
3x – 2y = 6 (1)
Tính giá trị của biểu thức ở vế trái của phương trình (1) tại x = 4; y = 3. Giá trị đó có bằng 6 hay không?
Trả lời:
Thay x = 4 và y = 3 vào vế trái của phương trình (1), ta có:
3.4 – 2.3 = 12 – 6 = 6.
Giá trị của vế trái của phương trình (1) tại x = 4; y = 3 bằng 6.
Luyện tập, vận dụng 2: Nêu hai nghiệm của phương trình: 6x – 5y = 11.
Trả lời:
Để tìm hai nghiệm của phương trình 6x – 5y = 11, chúng ta có thể chọn một giá trị của x và tính tương ứng giá trị của y, hoặc ngược lại.
Ví dụ
Khi x = 1, thay x = 1 vào phương trình ta có:
6.1 – 5y = 11
6 – 5y = 11
– 5y = 5
y = – 1
Vậy một nghiệm của phương trình là (1, – 1).
Khi y = 0, thay y = 0 vào phương trình ta có:
6x – 5.0 = 11
6x = 11
x = ![]()
Vậy một nghiệm của phương trình là (![]()
Do đó, hai nghiệm của phương trình 6x – 5y = 11 là (1, – 1) và (![]()
II. Hệ hai phương trình bậc nhất hai ẩn
Hoạt động 3: Hai bạn Dũng, Huy vào siêu thị mua vở và bút bi để ủng hộ các bạn học sinh vùng lũ lụt. Bạn Dũng mua 5 quyển vở và 3 chiếc bút bi với tổng số tiền phải trả là 39 000 đồng. Bạn Huy mua 6 quyển vở và 2 chiếc bút bi với tổng số tiền phải trả là 42 000 đồng. Giả sử giá của mỗi quyển vở là x đồng (x > 0), giá của mỗi chiếc bút bi là y đồng (y > 0).
a) Viết hai phương trình bậc nhất hai ẩn x, y lần lượt biểu thị tổng số tiền phải trả của bạn Dũng, bạn Huy.
b) Cặp số (x; y) = (6 000; 3 000) có phải là nghiệm của từng phương trình bậc nhất đó hay không? Vì sao?
Trả lời:

Luyện tập, vận dụng 3: Cho ví dụ về hệ hai phương trình bậc nhất hai ẩn.
Trả lời:
Một ví dụ về hệ hai phương trình bậc nhất hai ẩn là
Luyện tập, vận dụng 4: Cho hệ phương trình:
Kiểm tra xem cặp số nào sau đây là nghiệm của hệ phương trình đã cho:
a) (3; 3);
b) (4; 2).
Trả lời:
a) Thay (3 ; 3) vào hệ phương trình
![]()
= ![]()
Vậy (3 ; 3) không phải là nghiệm của hệ phương trình đã cho
b) Thay (4 ; 2) vào hệ phương trình
![]()
=![]()
Vậy (4 ; 2) là nghiệm của hệ phương trình đã cho.
Bài tập
Bài tập 1: Trong các cặp số (8; 1), (–3; 6), (4; –1), (0; 2), cho biết cặp số nào là nghiệm của mỗi phương trình sau:
a) x – 2y = 6;
b) x + y = 3.
Trả lời:

Bài tập 2: Cho hệ phương trình:
Trong các cặp số sau, cặp số nào là nghiệm của hệ phương trình đã cho?
a) (3; –1).
b) (1; 0).
Trả lời:
a) Thay x = 3 và y = –1 vào mỗi phương trình trong hệ, ta có:
3 + 2.(–1) = 1;
3.3 – 2.(–1) = 11 ≠ 3.
Do đó, cặp số (3; –1) không là nghiệm của phương trình thứ hai trong hệ.
Vậy cặp số (3; –1) không là nghiệm của hệ phương trình đã cho.
b) Thay x = 1 và y = 0 vào mỗi phương trình trong hệ, ta có:
1 + 2.0 = 1;
3.1 – 2.0 = 3.
Do đó, cặp số (1; 0) là nghiệm của từng phương trình trong hệ.
Vậy cặp số (1; 0) là nghiệm của hệ phương trình đã cho.
Bài tập 3: Nhân dịp tết Trung thu, một doanh nghiệp dự định sản xuất hai loại bánh: bánh nướng và bánh dẻo. Lượng đường cần cho mỗi chiếc bánh nướng, bánh dẻo lần lượt là 60 g, 50 g. Gọi x và y lần lượt là số lượng bánh nướng và bánh dẻo mà doanh nghiệp dự định sản xuất để lượng đường sản xuất bánh là 500 kg. Viết phương trình bậc nhất hai ẩn x, y biểu thị lượng đường để sản xuất hai loại bánh và chỉ ra ba nghiệm của phương trình đó.

Trả lời:
Đổi đơn vị: 500kg = 500000g
Lượng đường cần cho mỗi chiếc bánh nướng là 60g
Lượng đường cần cho mỗi chiếc bánh dẻo là 50g
Ta có 60x + 50y = 500000
Hay 6x + 5y = 50000
Lưu ý: x, y là số chiếc bánh nướng và bánh dẻo nên x và y là số nguyên dương
y = ![]()
(Vì vậy để chọn x nguyên và là bội của 5 để y nguyên)
Chọn x = 5000 suy ra y = 4000 ta được cặp nghiệm (5000 ; 4000)
Chọn y = 4000 suy ra y = 5200 ta được cặp nghiệm (4000 ; 5200)
Chọn x = 6000 suy ra y = 2800 ta được cặp nghiệm (6000, 2800).
Bài tập 4: Năm bạn Châu, Hà, Khang, Minh, Phong cùng đi mua sticker để trang trí vở. Có hai loại sticker: loại I giá 2 nghìn đồng/chiếc và loại II giá 3 nghìn đồng/chiếc. Mỗi bạn mua 1 chiếc và tổng số tiền năm bạn phải trả là 12 nghìn đồng. Gọi x và y lần lượt là số sticker loại I và loại II mà năm bạn đã mua.
a) Viết hệ hai phương trình bậc nhất hai ẩn x, y biểu thị mối quan hệ giữa các đại lượng.
b) Cặp số (3; 2) có phải là nghiệm của hệ phương trình ở câu a hay không? Vì sao?
Trả lời:

Bài tập 5: Để chuẩn bị cho buổi liên hoan của gia đình, bác Ngọc mua hai loại thực phẩm là thịt lợn và cá chép. Giá tiền thịt lợn là 130 nghìn đồng/kg, giá tiền cá chép là 50 nghìn đồng/kg. Bác Ngọc đã chi 295 nghìn để mua 3,5 kg hai loại thực phẩm trên. Gọi x và y lần lượt là số kilôgam thịt lợn và cá chép mà bác Ngọc đã mua.
a) Viết hệ hai phương trình bậc nhất hai ẩn x, y biểu thị mối quan hệ giữa các đại lượng.
b) Cặp số (1,5; 2) có phải là nghiệm của hệ phương trình ở câu a hay không? Vì sao?
Trả lời:
a) Bác Ngọc đã mua 3,5 kg hai loại thực phẩm (thịt lợn và cá chép) nên ta có phương trình: x + y = 3,5. (1)
Số tiền bác Ngọc đã chi để mua x kilôgam thịt lợn là 130x (nghìn đồng).
Số tiền bác Ngọc đã chi để mua y kilôgam cá chép là 50y (nghìn đồng).
Theo bài, bác Ngọc đã chi 295 nghìn để mua hai loại thực phẩm trên nên ta có phương trình: 130x + 50y = 295. (2)
Từ (1) và (2) ta có hệ phương trình bậc nhất hai ẩn x, y biểu thị mối quan hệ giữa các đại lượng:
b) Thay x = 1,5 và y = 2 vào mỗi phương trình trong hệ ta có:
1,5 + 2 = 3,5;
130.1,5 + 50.2 = 195 + 100 = 295.
Do đó, cặp số (1,5; 2) là nghiệm của từng phương trình trong hệ.
Vậy cặp số (1,5; 2) là nghiệm của hệ phương trình ở câu a.
Bài tập 6: Người ta cần sơn hai loại sản phẩm A, B bằng hai loại sơn: sơn xanh, sơn vàng. Lượng sơn để sơn mỗi loại sản phẩm đó được cho ở Bảng 1 (đơn vị: kg/ 1 sản phẩm).
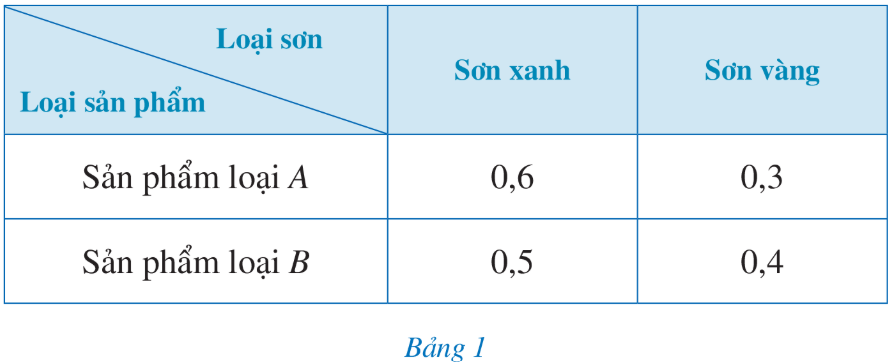
Người ta dự định sử dụng 85 kg sơn xanh và 50 kg sơn vàng để sơn tất cả các sản phẩm của hai loại đó. Gọi x, y lần lượt là số sản phẩm loại A, số sản phẩm loại B được sơn.
a) Viết hệ hai phương trình bậc nhất hai ẩn x, y biểu thị mối quan hệ giữa các đại lượng.
b) Cặp số (100; 50) có phải là nghiệm của hệ phương trình ở câu a hay không? Vì sao?
Trả lời:
Gọi x, y lần lượt là số sản phẩm loại A, số sản phẩm loại B được sơn.
Sử dụng 85kg sơn xanh để sơn hai loại sản phẩm A, B nên ta có:
0,6x + 0,5y = 85
Sử dụng 50kg sơn vàng để sơn hai loại sản phẩm A, B nên ta có:
0,3x + 0,4y = 50
Vậy x, y là nghiệm của hệ phương trình ![]()
b) Thay x = 100 và y = 50 vào từng phương trình của hệ, ta có:
0,6.100 + 0,5.50 = 85
0,3.100 + 0,4.50 = 50
Vậy cặp số (100 ; 50) là nghiệm của hệ phương trình ở câu a).
