Giải SGK Toán 10 Chân trời sáng tạo Bài 1: Mệnh đề

Hoạt động khởi động: Hãy theo dõi tình huống sau đây:

Bạn có thể phát biểu định lí theo cách khác?

Sau bài học này, bạn còn có thể đưa ra những cách phát biểu khác nữa.

Trả lời:

Tam giác ABC cân là điều kiện đủ để hai góc ở đáy của tam giác ABC bằng nhau.

Tam giác ABC có hai góc ở đáy bằng nhau là điều kiện cần để có tam giác ABC cân. 

…

1. Mệnh đề

Hoạt động khám phá 1: Xét các câu sau đây:

(1) 1 + 1 = 2.

(2) Dân ca Quan họ là di sản văn hóa phi vật thể đại diện cho nhân loại.

(3) Dơi là một loài chim.

(4) Nấm có là một loài thực vật không?

(5) Hoa hồng đẹp nhất trong các loài hoa.

(6) Trời ơi, nóng quá!

Trong những câu trên, 

a) Cây nào là khẳng định đúng, câu nào là khẳng định sai?

b) Câu nào không phải khẳng định?

c) Câu nào là khẳng định, nhưng không thể xác định nó đúng hay sai?

Trả lời:

a) Câu là khẳng định đúng:

(1) 1+1=2.

(2) Dân ca Quan họ là di sản văn hóa phi vật thể đại diện của nhân loại.

Câu là khẳng định sai:

(3) Dơi là một loài chim

b) Câu không phải là khẳng định:

(4) Nấm có phải là một loài thực vật không?

(6) Trời ơi, nóng quá!

c) Câu là khẳng định, nhưng không thể xác định nó đúng hay sai:

(5) Hoa hồng đẹp nhất trong các loài hoa.

Thực hành 1: Trong các câu sau, câu nào là mệnh đề?

a) $\sqrt{2}$ là số vô tỉ;

b) $\frac{1}{\sqrt{2}}+\frac{1}{\sqrt{3}}+\mathrm{...}+\frac{1}{\sqrt{10}}>2$;

c) 100 tỉ là số rất lớn;

d) Trời hôm nay đẹp quá!

Trả lời:

- Câu là mệnh đề là a và b

Thực hành 2: Xét tính đúng sai của mệnh đề sau:

a) Vịnh Hạ Long là di sản thiên nhiên thế giới;

b) $\sqrt{{\left(-5\right)}^2}=-5;$

c) 52 + 122 = 132

Trả lời:

Năm 1994 vùng lõi của vịnh Hạ Long được UNESCO công nhận là Di sản Thiên nhiên Thế giới. Do đó mệnh đề a) là mệnh đề đúng. 

Ta có: $\sqrt{{\left(-5\right)}^2}=\left|-5\right|=5$. Do đó mệnh đề b) là mệnh đề sai.

Ta có 52 + 122 = 25 + 144 = 169 = 132. Do đó mệnh đề c) là mệnh đề đúng.

2. Mệnh đề chứa biến

Hoạt động khám phá 2: Xét câu “n chia hết cho 5” (n là số tự nhiên).

a) Có thể khẳng định câu trên là đúng hay sai không?

b) Tìm hai giá trị của n sao cho câu trên là khẳng định đúng, hai giá trị của n sao cho câu trên là khẳng định sai.

Trả lời:

a) Không thể khẳng định câu trên là đúng hay sai.

b)

+) n = 0 hoặc n =5 thì “n chia hết cho 5” là khẳng định đúng.

+) n = 2 hoặc n =34 thì “n chia hết cho 5” là khẳng định sai.

Thực hành 3: Với mỗi mệnh đề chứa biến sau, tìm những giá trị của biến để nhận được một mệnh đề đúng và một mệnh đề sai.

a) P(x): “x2 = 2”;

b) Q(x): “x2 + 1 > 0”;

c) R(n): “n + 2 chia hết cho 3” (n là số tự nhiên). 

Trả lời:

a.

• Mệnh đề đúng khi x = ±2–√
• Mệnh đề sai khi x ≠±2–√

b. Mệnh đề luôn đúng với mọi giá trị của x.

c.

• Với n = 1, 4, 7, 10... thì mệnh đề đúng
• Với n = 0, 2, 3, 5, 6, 8... thì mệnh đề sai.

3. Mệnh đề phủ định

Hoạt động khám phá 3: Xét các cặp mệnh đề nằm cùng dòng của bảng (có hai cột P và $\overline{P}$) sau đây

Nêu nhận xét về tính đúng sai của hai mệnh đề cùng cặp.

Trả lời:

+) Dơi là thú chứ không phải là chim vì dơi đẻ con và nuôi con bằng sữa. Do đó P là mệnh đề sai còn $\overline{P}$ là mệnh đề đúng.

+) Ta có: π ≈ 3,141592654…

Suy ra π là một số vô tỉ. Do đó P là mệnh đề đúng còn $\overline{P}$ là mệnh đề sai.

+) Ta có: ${\left(\sqrt{2}+\sqrt{3}\right)}^2=5+2\sqrt{6}$ và 52 = 25 = 5 + 2.10

Vì $5+2.10>5+2\sqrt{6}$ nên ${\left(\sqrt{2}+\sqrt{3}\right)}^2>5^2$

Mà $\sqrt{2}+\sqrt{3};5>0$ suy ra $\sqrt{2}+\sqrt{3}>5$

Do đó P là mệnh đề đúng còn $\overline{P}$ là mệnh đề sai.

+) Ta có: $\sqrt{2}.\sqrt{18}=\sqrt{2.18}=\sqrt{36}=6$

Do đó P là mệnh đề đúng còn $\overline{P}$ là mệnh đề sai.

Thực hành 4: Phát biểu mệnh đề phủ định của các mệnh đề sau. Xét tính đúng sai của mỗi mệnh đề và mệnh đề phủ định của nó.

a) Paris là thủ đô của nước Anh;

b) 23 là số nguyên tố;

c) 2 021 chia hết cho 3;

d) Phương trình x2 – 3x + 4 = 0 vô nghiệm.

Trả lời:

4. Mệnh đề kéo theo

Hoạt động khám phá 4: Xét hai mệnh đề sau:

(1) Nếu ABC là tam giác đều thì nó là tam giác cân;

(2) Nếu 2a – 4 > 0 thì a > 2.

a) Xét tính đúng sai của mỗi mệnh đề trên.

b) Mỗi mệnh đề trên đều có dạng “Nếu P thì Q”. Chỉ ra P và Q ứng với mỗi mệnh đề đó.

Trả lời:

a. Hai mệnh đề đều đúng.

b.

• P là "ABC là tam giác đều" và "2a - 4 > 0".
• Q là "nó là tam giác cân" và "a > 2".

Thực hành 5: Xét hai mệnh đề:

P: “Hai tam giác ABC và A’B’C’ bằng nhau”;

Q: “Hai tam giác ABC và A’B’C’ có diện tích bằng nhau”.

a) Phát biểu mệnh đề P ⇒ Q.

b) Mệnh đề P ⇒ Q có phải là một định lí không? Nếu có, sử dụng thuật ngữ “điều kiện cần”, “điều kiện đủ” để phát biểu định lí này theo hai cách khác nhau.

Trả lời:

a) Mệnh đề P ⇒ Q được phát biểu như sau:

P ⇒ Q: “Nếu hai tam giác ABC và A’B’C’ bằng nhau thì hai tam giác ABC và A’B’C’ có diện tích bằng nhau”.

b) Mệnh đề P ⇒ Q là mệnh đề đúng. Do đó mệnh đề P  Q là một định lí.

Hai tam giác ABC và A’B’C’ bằng nhau là điều kiện đủ để có hai tam giác ABC và A’B’C’ có diện tích bằng nhau.

Hai tam giác ABC và A’B’C’ có diện tích bằng nhau là điều kiện cần để có hai tam giác ABC và A’B’C’ bằng nhau.

5. Mệnh đề đảo. Hai mệnh đề tương đương

Hoạt động khám phá 5: Xét hai mệnh đề dạng P ⇒ Q sau:

“Nếu ABC là tam giác đều thì nó có hai góc bằng 600”

“Nếu a = 2 thì a2 – 4 = 0”.

a) Chỉ ra P, Q và xét tính đúng sai của mỗi mệnh đề trên.

b) Với mỗi mệnh đề đã cho, phát biểu mệnh đề Q ⇒ P và xét tính đúng sai của nó.

Trả lời:

Thực hành 6: Xét hai mệnh đề:

P: “Tứ giác ABCD là hình vuông”;

Q: “Tứ giác ABCD là hình chữ nhật có hai đường chéo vuông góc với nhau”.

a) Phát biểu mệnh đề P  Q và mệnh đề đảo của nó.

b) Hai mệnh đề P và Q có tương đương không? Nếu có, sử dụng thuật ngữ “điều kiện cần và đủ” hoặc “khi và chỉ khi” để phát biểu định lí P ⇔ Q theo hai cách khác nhau.

Trả lời:

a. "Nếu tứ giác ABCD là hình vuông thì tứ giác ABCD là hình chữ nhật có hai đường chéo vuông góc với nhau."

Mệnh đề đảo là: "Nếu tứ giác ABCD là hình chữ nhật có hai đường chéo vuông góc với nhau thì tứ giác ABCD là hình vuông".

b. Hai mệnh đề P và Q có tương đương.

+ Cách 1: "Tứ giác ABCD là hình chữ nhật có hai đường chéo vuông góc với nhau là điều kiện cần và đủ để tứ giác ABCD là hình vuông".

+ Cách 2: "Tứ giác ABCD là hình vuông khi và chỉ khi tứ giác ABCD là hình chữ nhật có hai đường chéo vuông góc với nhau". 

6. Mệnh đề chứa kí hiệu ∀,∃

Hoạt động khám phá 6: Xét tính đúng sai của các mệnh đề sau:

(1) Với mọi số tự nhiên x, $\sqrt{x}$ là số vô tỉ;

(2) Bình phương mọi số thực đều không âm;

(3) Có số nguyên cộng với chính nó bằng 0;

(4) Có số tự nhiên n sao cho 2n – 1 = 0.

Trả lời:

(1) Đây là mệnh đề sai, vì:

Chọn x = 9 thì $\sqrt{x}=\sqrt{9}=3$ là một số hữu tỉ. 

(2) Đây là mệnh đề đúng, vì:

Với mọi x ∈ ℝ ta có x2 ≥ 0 .

(3) 0 là số nguyên và 0 + 0 = 0. Do đó mệnh đề này là đúng.

(4) Xét 2n – 1 = 0 $\iff n=\frac{1}{2}$ là một số hữu tỉ không phải là số tự nhiên. Do đó không tồn tại số tự nhiên n nào thỏa mãn 2n – 1 = 0. Vì vậy mệnh đề này sai.

Thực hành 7: Sử dụng kí hiệu $\forall ,\exists$ để viết các mệnh đề sau:

a) Mọi số thực cộng với số đối của nó đều bằng 0;

b) Có một số tự nhiên mà bình phương bằng 9.

Trả lời:

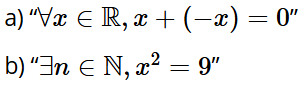
Thực hành 8: Xét tính đúng sai và viết mệnh đề phủ định của các mệnh đề sau:

a) $\forall x\in R,x^2>0;$

b) $\exists x\in R,x^2=5x-4;$

c) $\exists x\in Z,2x+1=0.$

Trả lời:

a. Mệnh đề sai.

Mệnh đề phủ định: ∀ x ∈R, x2 ≤ 0.

b. Mệnh đề đúng.

Mệnh đề phủ định: ∃ x ∈R, x2 ≠ 5x - 4

c. Mệnh đề sai.

Mệnh đề phủ định: ∃ x ∈Z, 2x + 1 ≠ 0

Bài tập

Bài tập 1: Trong các khẳng định sau, khẳng định nào là mệnh đề, khẳng định nào là mệnh đề chứa biến?

a) 3 + 2 > 5;

b) 1 – 2x = 0;

c) x – y = 2;

d) 1 – $\sqrt{2}$ < 0.

Trả lời:

+) 3 + 2 > 5 là một khẳng định có thể xác định được tính đúng sai. Do đó a) là mệnh đề.

+) 1 – 2x = 0 không xác định được tính đúng sai mà phụ thuộc vào giá trị của biến x. Do đó b) là mệnh đề chứa biến.

+) x – y = 2 không xác định được tính đúng sai mà phụ thuộc vào giá trị của biến x và y. Do đó c) là mệnh đề chứa biến.

+) 1 – $\sqrt{2}$ < 0 là một khẳng định có thể xác định được tính đúng sai. Do đó d) là mệnh đề.

Vậy các mệnh đề là a), d) và các mệnh đề chứa biến là b), c).

Bài tập 2: Xét tính đúng sai của các mệnh đề sau và phát biểu mệnh đề phủ định của chúng.

a) 2 020 chia hết cho 3;

b) π < 3,15;

c) Nước ta hiện nay có 5 thành phố trực thuộc Trung ương;

d) Tam giác có hai góc bằng 450 là tam giác vuông cân.

Trả lời:

a. Mệnh đề sai.

Mệnh đề phủ định là: "2020 không chia hết cho 3".

b. Mệnh đề đúng.

Mệnh đề phủ định là: "π≥  3,15".

c. Mệnh đề đúng.

Mệnh đề phủ định là: "Nước ta hiện nay không có 5 thành phố trực thuộc trung ương."

d. Mệnh đề đúng.

Mệnh đề phủ định là: "Tam giác có hai góc bằng 45∘ không là tam giác vuông cân".

Bài tập 3: Xét hai mệnh đề:

P: “Tứ giác ABCD là hình bình  hành”;

Q: “Tứ giác ABCD có hai đường chéo cắt nhau tại trung điểm mỗi đường”.

a) Phát biểu mệnh đề P ⇒ Q và xét tính đúng sai của nó.

b) Phát biểu mệnh đề đảo của mệnh đề P ⇒ Q.

Trả lời:

a) Mệnh đề P ⇒ Q: “Nếu tứ giác ABCD là hình bình hành thì nó có hai đường chéo cắt nhau tại trung điểm của mỗi đường”. Mệnh đề này đúng vì “hai đường chéo cắt nhau tại trung điểm của mỗi đường” là tính chất của hình hình hành.

b) Mệnh đề đảo của mệnh đề P ⇒ Q là mệnh đề Q ⇒ P, được phát biểu là: “Nếu tứ giác ABCD có hai đường chéo cắt nhau tại trung điểm của mỗi đường thì nó là hình bình hành”.

Bài tập 4: Cho các định lí:

P: “Nếu hai tam giác bằng nhau thì diện tích của chúng bằng nhau”;

Q: “Nếu a < b thì a + c < b + c” (a, b, c ∈ ℝ).

a) Chỉ ra giả thiết và kết luận của mỗi định lí;

b) Phát biểu lại mỗi định lí đã cho, sử dụng thuật ngữ “điều kiện cần” hoặc “điều kiện đủ”.

c) Mệnh đề đảo của mỗi định lí đó có là định lí không?

Trả lời:

a) Chỉ ra giả thiết và kết luận của mỗi định lí;

Xét định lý P: “Nếu hai tam giác bằng nhau thì diện tích của chúng bằng nhau” có:

Giả thiết: Nếu hai tam giác bằng nhau.

Kết luận: Diện tích của chúng bằng nhau.

Xét định lý Q: “Nếu a < b thì a + c < b + c” (a, b, c ∈ ℝ), có:

Giả thiết: a < b

Kết luận: a + c < b + c

b) Phát biểu lại mỗi định lí đã cho, sử dụng thuật ngữ “điều kiện cần” hoặc “điều kiện đủ”:

Bằng thuật ngữ “điều kiện cần” hoặc “điều kiện đủ”, các định lý đã cho được phát biểu như sau:

Định lý P:

Hai tam giác bằng nhau là điều kiện đủ để diện tích của chúng bằng nhau.

Hai tam giác có diện tích bằng nhau là điều kiện cần để hai tam giác bằng nhau.

Định lý Q:

a < b là điều kiện đủ để có a + c < b + c.

a + c < b + c là điều kiện cần để có a < b.

c) +) Mệnh đề đảo của định lí P là: “Nếu hai tam giác có diện tích bằng nhau thì hai tam giác đó bằng nhau”.

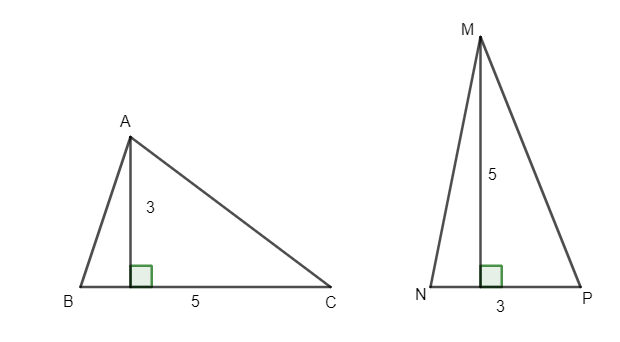
Mệnh đề này là mệnh đề sai, chẳng hạn hai tam giác sau ABC và MNP có cùng diện tích là 7,5 (đvdt) nhưng hai tam giác này không bằng nhau.

Do đó mệnh đề đảo của định lí P không là định lí.

+) Mệnh đề đảo của định lí Q là: “Nếu a + c < b + c thì a < b”.

Mệnh đề này là một mệnh đề đúng, vì:

Ta có: a + c < b + c 

⇔ a + c + (-c) < b + c + (-c) (liên hệ giữa thứ tự và phép cộng)

⇔ a < b.

Do đó mệnh đề đảo của định lí Q là một định lí.

Bài tập 5: Sử dụng thuật ngữ “điều kiện cần và đủ”, phát biểu các định lí sau:

a) Một phương trình bậc hai có hai nghiệm phân biệt khi và chỉ khi biệt thức của nó dương;

b) Một hình bình hành là hình thoi thì nó có hai đường chéo vuông góc với nhau và ngược lại.

Trả lời:

a. Biệt thức của phương trình bậc hai dương là điều kiện cần và đủ để phương trình có hai nghiệm phân biệt.

b. Hình bình hành có hai đường chéo vuông góc với nhau là điều kiện cần và đủ để hình bình hành là hình thoi.

Bài tập 6: Cho các mệnh đề sau:

P: “Giá trị tuyệt đối của mọi số thực đều lớn hơn hoặc bằng chính nó”;

Q: “Có số tự nhiên sao cho bình phương của nó bằng 10”;

R: “Có số thực x sao cho x2 + 2x – 1 = 0”.

a) Xét tính đúng sai của mỗi mệnh đề trên.

b) Sử dụng kí hiệu ∀, ∃ để viết lại các mệnh đề đã cho.

Trả lời:

Bài tập 7: Xét tính đúng, sai và viết mệnh đề phủ định của các mệnh đề sau đây:

a) $\exists x\in N$ , x + 3 = 0;

b) ∀x ∈ ℝ , x2 + 1 ≥ 2x;

c) $\forall a\in R,\sqrt{a^2}=a.$

Trả lời:

a) Xét x + 3 = 0

⇔ x = -3 

Nhưng – 3 không là số tự nhiên. 

Do đó không tồn tại số tự nhiên x thỏa mãn x + 3 = 0.

Vậy mệnh đề a) sai.

Mệnh đề phủ định a) là: $\forall x\in N$, x + 3 ≠ 0.

b) Xét bất phương trình: x2 + 1 ≥ 2x

⇔ x2 – 2x + 1 ≥ 0

⇔ (x – 1)2 ≥ 0 (luôn đúng với mọi x)

Do đó với mọi số thực x đề thỏa mãn x2 + 1 ≥ 2x.

Vậy mệnh đề b) đúng.

Mệnh đề phủ định của mệnh đề b) là: $\exists x\in R$, x2 + 1 < 2x.

c) $\forall a\in R,\sqrt{a^2}=a.$

Ta có hằng đẳng thức: $\sqrt{a^2}=\left|a\right|$

Nếu a ≥ 0 thì $\sqrt{a^2}=\left|a\right|=a$

Nếu a < 0 thì $\sqrt{a^2}=\left|a\right|=-a$

Do đó với a ≥ 0 thì $\sqrt{a^2}=a$

Vậy mệnh đề c) sai. 

Mệnh đề phủ định của mệnh đề c) là: $\exists a\in R,\sqrt{a^2}\ne a.$