1. Góc giữa hai vectơ
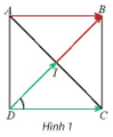
Hoạt động khám phá 1: Cho hình vuông ABCD có tâm I (Hình 1).
a) Tính .
b) Tìm hai vectơ cùng có điểm đầu là D và điểm cuối lần lượt là I và C.
c) Tìm hai vectơ cùng có điểm đầu là D và lần lượt bằng và .
Trả lời:

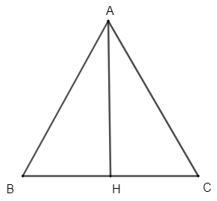
Thực hành 1: Cho tam giác đều ABC có H là trung điểm của cạnh BC. Tìm các góc: ,.
Trả lời:
Tam giác ABC đều có H là trung điểm BC nên AH là đường trung tuyến đồng thời là đường cao của tam giác.
+ Ta có: (tam giác ABC đều).
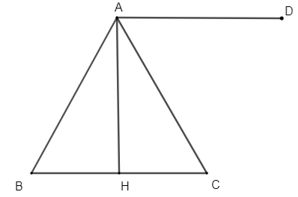
+ Qua A kẻ đường thẳng song song với BC về phía C, lấy điểm D sao cho AD = BC.
Khi đó ta có .
Suy ra: .
Lại có: (AD // BC, hai góc so le trong)
Nên .
Do đó: .
+ Do AH vuông góc với BC nên , do đó .
+ Do hai vectơ và cùng hướng nên .
+ Do hai vectơ và ngược hướng nên .
2. Tích vô hướng của hai vectơ
Hoạt động khám phá 2: Một người dùng một lực có cường độ 10N kéo môt chiếc xe đi quãng đường dài 100 m. Tính công sinh bởi lực , biết rằng góc giữa vectơ và hướng di chuyển là 45°. (Công A (đơn vị: J) bằng tích của ba đại lượng: cường độ của lực , độ dài quãng đường và côsin của góc giữa hai vectơ và độ dịch chuyển ).
Trả lời:
A = |
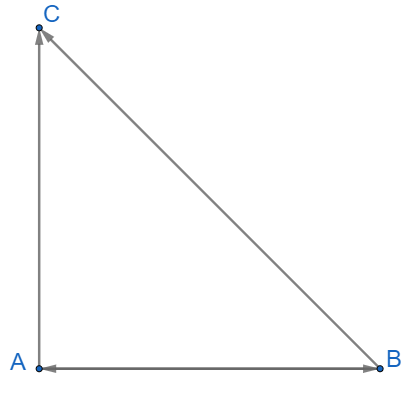
Thực hành 2: Cho tam giác ABC vuông cân tại A, cạnh huyền bằng . Tính các tích vô hướng: .
Trả lời:
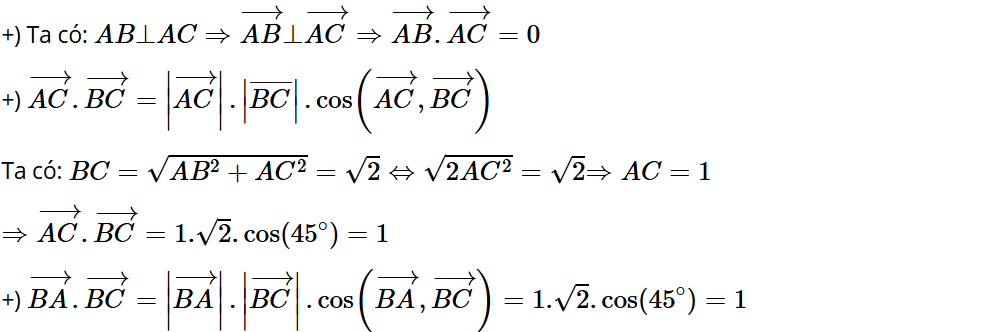
Thực hành 3: Hai vectơ và có độ dài lần lượt là 3 và 8 và có tích vô hướng là . Tính góc giữa hai vectơ và .
Trả lời:
Ta có: .
Mà
Suy ra: .
Do đó: .
Vậy góc giữa hai vectơ và là 45°.
Vận dụng 1: Một người dùng một lực có độ lớn là 20 N kéo một vật dịch chuyển một đoạn 50 m cùng hướng với . Tính công sinh bởi lực .
Trả lời:
A = 20. 50.
3. Tính chất của tích vô hướng
Thực hành 4: Cho hai vectơ vuông góc, cùng có độ dài bằng 1.
a) Tính: .
b) Cho . Tính tích vô hướng và tính góc .
Trả lời:
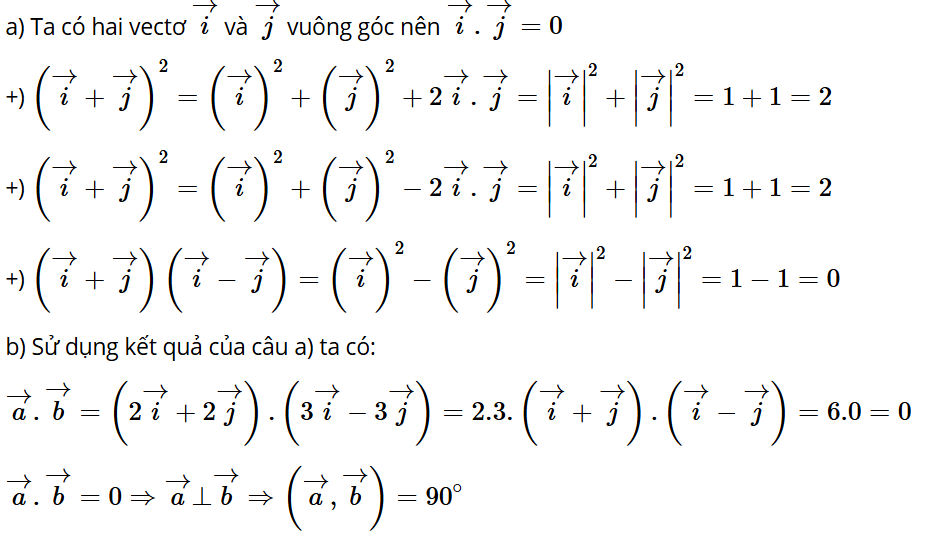
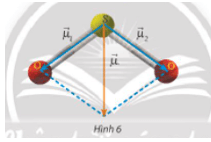
Vận dụng 2: Phân tử sulfur dioxide (SO2) có cấu tạo hình chữ V, góc liên kết gần bằng 120°. Người ta biểu diễn sự phân cực giữa nguyên tử S với mỗi nguyên tử O bằng các vectơ và có cùng phương với liên kết cộng hóa trị, có chiều từ nguyên tử S về mỗi nguyên tử O và cùng có độ dài là 1,6 đơn vị (Hình 6). Cho biết vectơ tổng được dùng để biểu diễn sự phân cực của cả phân tử SO2. Tính độ dài của .
Trả lời:
Theo bài ra ta có: .
Do đó: = 1,6 . 1,6 . cos120° = – 1,28.
Vì nên để tính độ dài của , ta tính độ dài của vectơ tổng .
Ta có:
= 1,62 + 2 . (– 1,28) + 1,62 = 2,56
Suy ra .
Vậy .
Bài tập
Bài tập 1: Cho hình vuông ABCD có cạnh bằng a. Tính các tích vô hướng: .
Trả lời:
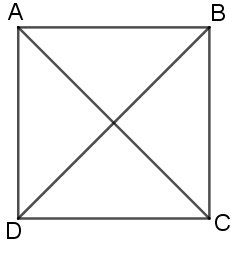
AB→ .AD→ = |AB→ |. |AD→ |. cos(AB→ ,AD→ ) = a. a.cos90∘ = 0AB→ .AC→ = |AB→ |. |AC→ |. cos(AB→ ,AC→ ) = a.2–√ a.cos45∘ =a2 AC→ .CB→ = |AC→ |. |CB→ |. cos(AC→ ,CB→ ) =2–√ a. a.cos135∘ =−a2 AC→ .BD→ = |AC→ |. |BD→ |. cos(AC→ ,BD→ ) =2–√ a.2–√ a.cos90∘ = 0
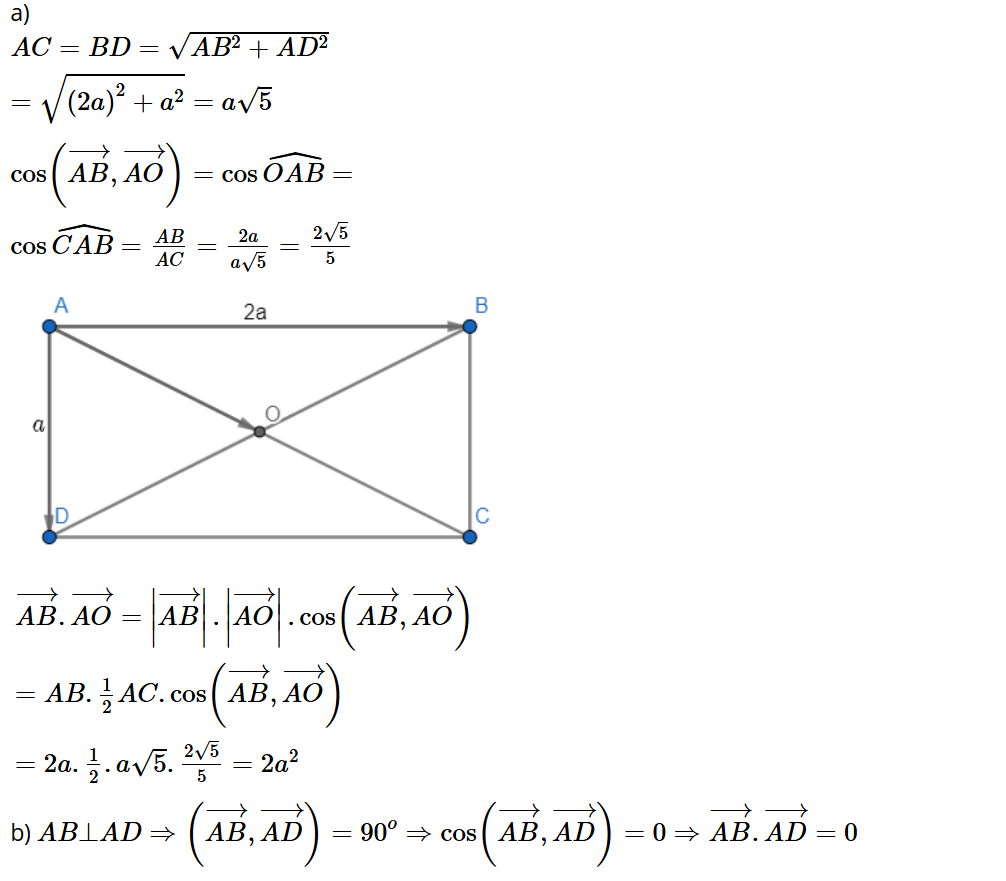
Bài tập 2: Cho hình chữ nhật ABCD có tâm O và cho AD = a, AB = 2a. Tính:
a) ;
b) .
Trả lời:
Bài tập 3: Cho ba điểm O, A, B thẳng hàng và OA = a, OB = b. Tính tích vô hướng trong hai trường hợp:
a) Điểm O nằm ngoài đoạn thẳng AB;
b) Điểm O nằm trong đoạn thẳng AB.
Trả lời:
a) Điểm O nằm ngoài đoạn thẳng AB
Khi đó hai vectơ và cùng hướng nên .
Do đó: .
b) Điểm O nằm trong đoạn thẳng AB
Khi đó hai vectơ và ngược hướng nên .
Do đó: .
Bài tập 4: Cho đoạn thẳng AB có O là trung điểm và cho điểm M tùy ý. Chứng minh rằng: .
Trả lời:
Ta có:
=
=
=
Vậy
Bài tập 5: Một người dùng một lực có độ lớn là 90 N làm một vật dịch chuyển một đoạn 100 m. Biết lực hợp với hướng dịch chuyển một góc 60°. Tính công sinh bởi lực .
Trả lời:

Bài tập 6: Cho hai vectơ có độ dài lần lượt là 3 và 4 và có tích vô hướng là – 6. Tính góc giữa hai vectơ đó.
Trả lời:
Giả sử hai vectơ đề bài cho là và .
Theo bài ra ta có: .
Ta có:
Suy ra: .
Vậy .