Giải SGK Toán 10 Chân trời sáng tạo Bài 2: Tổng và hiệu của hai vectơ - Giải SGK Toán 10 - Chân trời sáng tạo

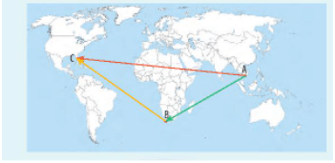
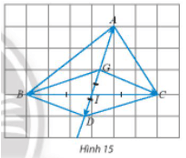
Hoạt động khởi động: Một kiện hàng được vận chuyển từ điểm A đến điểm B rồi lại được vận chuyển từ điểm B đến điểm C. Tìm vectơ biểu diễn tổng của hai độ dịch chuyển: $\vec{A B} + \vec{B C}$ .

Hoạt động khởi động trang 88 Toán 10 Tập 1 Chân trời sáng tạo | Giải Toán 10

Trả lời:

Vectơ biểu diễn tổng của hai độ dịch chuyển: AB→ + BC→ là vectơ AC→

1. Tổng của hai vectơ

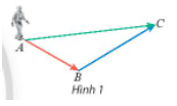
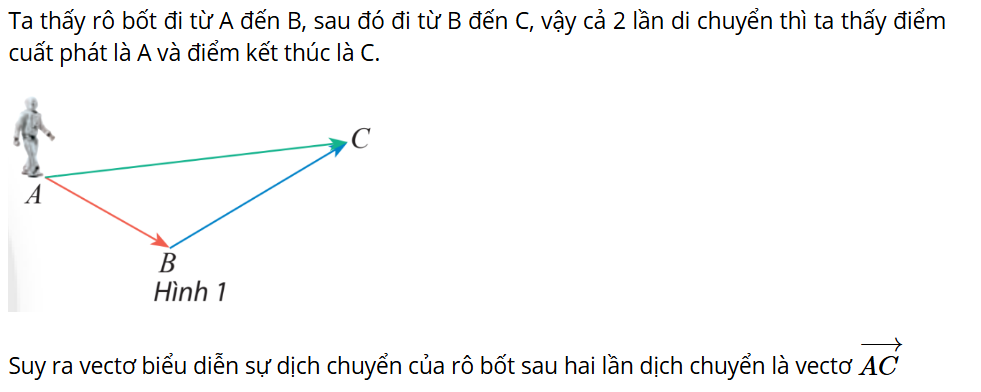
Hoạt động khám phá 1: Một rô bốt thực hiện liên tiếp hai chuyển động có độ dịch chuyển lần lượt được biểu diễn bởi hai vectơ $\vec{A B}$ và $\vec{B C}$ (Hình 1). Tìm vectơ biểu diễn độ dịch chuyển của rô bốt sau chuyển động trên.

Hoạt động khám phá 1 trang 88 Toán 10 Tập 1 Chân trời sáng tạo | Giải Toán 10

Trả lời:

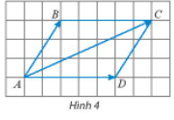
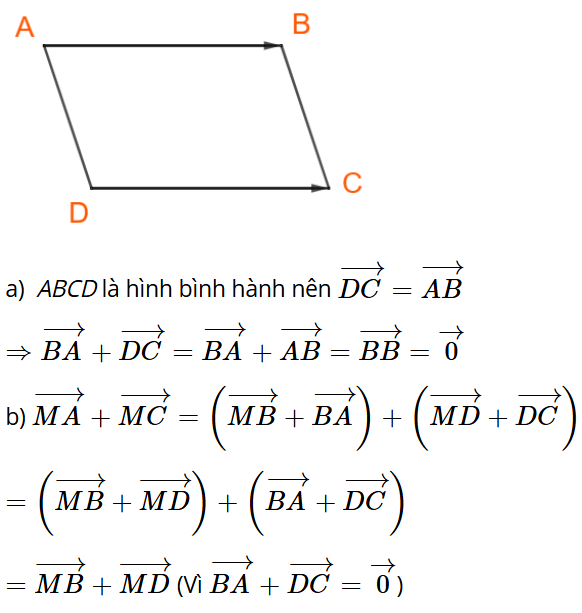
Hoạt động khám phá 2: Cho hình bình hành ABCD (Hình 4). Chứng minh rằng $\vec{A B} + \vec{A D} = \vec{A C}$ .

Hoạt động khám phá 2 trang 89 Toán 10 Tập 1 Chân trời sáng tạo | Giải Toán 10

Trả lời:

Do ABCD là hình bình hành nên $\vec{A D} = \vec{B C}$

Khi đó ta có: $\vec{A B} + \vec{A D} = \vec{A B} + \vec{B C} = \vec{A C }$ (theo quy tắc ba điểm).

Vậy $\vec{A B} + \vec{A D} = \vec{A C}$ .

Thực hành 1: Cho hình thang ABCD có hai đáy là AB và DC. Cho biết $\vec{a} = \vec{A C} + \vec{C B}; \vec{b} = \vec{D B} + \vec{B C}$ . Chứng minh hai vectơ $\vec{a}$ và $\vec{b}$ cùng hướng.

Trả lời:

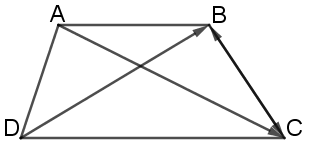
Giải bài 2 Tổng và hiệu của hai vectơ

Vì ABCD là hình thang có hai cạnh đấy AB và DC nên AB DC ⇒ AB→ cùng hướng với DC→.

Ta có: a⃗ = AC→ + CB→ = AB→

b⃗ = DB→ + BC→ = DC→

⇒ Hai vectơ a⃗ và b⃗ cùng hướng (đpcm).

Thực hành 2: Cho tam giác đều ABC có cạnh bằng a. Tìm độ dài của vectơ $\vec{A B} + \vec{A C}$ .

Trả lời:

Dựng hình bình hành ABDC.

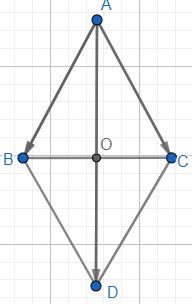
Áp dụng quy tắc hình bình hành vào ABDC ta có:

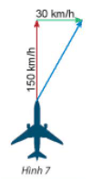
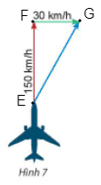
Vận dụng 1: Một máy bay có vectơ vận tốc chỉ theo hướng bắc, vận tốc gió là một vectơ theo hướng đông như Hình 7. Tính độ dài vectơ tổng của hai vectơ nói trên.

Vận dụng 1 trang 90 Toán 10 Tập 1 Chân trời sáng tạo | Giải Toán 10

Trả lời:

Đặt vectơ vận tốc của máy bay là $\vec{E F}$ , vectơ vận tốc gió là $\vec{F G}$ như hình sau:

Một máy bay có vectơ vận tốc chỉ theo hướng bắc, vận tốc gió là một vectơ

Ta có: $E F = |\vec{E F}| = 150; F G = |\vec{F G}| = 30$ .

Theo quy tắc ba điểm ta có: $\vec{E F} + \vec{F G} = \vec{E G}$ .

Do đó: $|\vec{E F} + \vec{F G}| = |\vec{E G}| = E G$ .

Xét tam giác EFG vuông tại F, áp dụng định lí Pythagore ta có:

EG2 = EF2 + FG2 = 1502 + 302 = 23400

Suy ra $EG = 30 \sqrt{26}$ .

Vậy $|\vec{E F} + \vec{F G}| = |\vec{E G}| = E G = 30 \sqrt{26}$ (km/h).

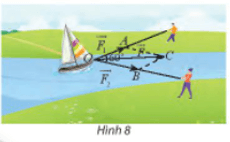
Vận dụng 2: Hai người cùng kéo một con thuyền với hai lực $\vec{F_{1}} = \vec{O A}, \vec{F_{2}} = \vec{O B}$ có độ lớn lần lượt là 400 N, 600 N (Hình 8). Cho biết góc giữa hai vectơ là 60°. Tìm độ lớn của vectơ hợp lực $\vec{F}$ là tổng của hai lực $\vec{F_{1}}$ và $\vec{F_{2}}$ .

Vận dụng 2 trang 90 Toán 10 Tập 1 Chân trời sáng tạo | Giải Toán 10

Trả lời:

Áp dụng định lí côsin, ta có:

OC = (F1)2+(F2)2−2F1F2.cos120∘−−−−−−−−−−−−−−−−−−−−−−−−√

= 4002+6002−2.400.600.cos120∘−−−−−−−−−−−−−−−−−−−−−−−−−√≈ 871,78 (N)

⇒ |F⃗ | = |OC→| ≈ 871,78(N)

2. Tính chất của phép cộng các vectơ

Hoạt động khám phá 2: Cho ba vectơ $\vec{a}, \vec{b}, \vec{c}$ được biểu diễn như Hình 9. Hãy hoàn thành các phép cộng vectơ sau và so sánh các kết quả tìm được:

a) $\vec{a} + \vec{b} = \vec{A B} + \vec{B C} = ?$ ;

$\vec{b} + \vec{a} = \vec{A E} + \vec{E C} = ?$

b) $(\vec{a} + \vec{b}) + \vec{c} = (\vec{A B} + \vec{B C}) + \vec{C D} = \vec{A C} + \vec{C D} = ?$ ;

$\vec{a} + (\vec{b} + \vec{c}) = \vec{A B} + (\vec{B C} + \vec{C D}) = \vec{A B} + \vec{B D} = ?$

Trả lời:

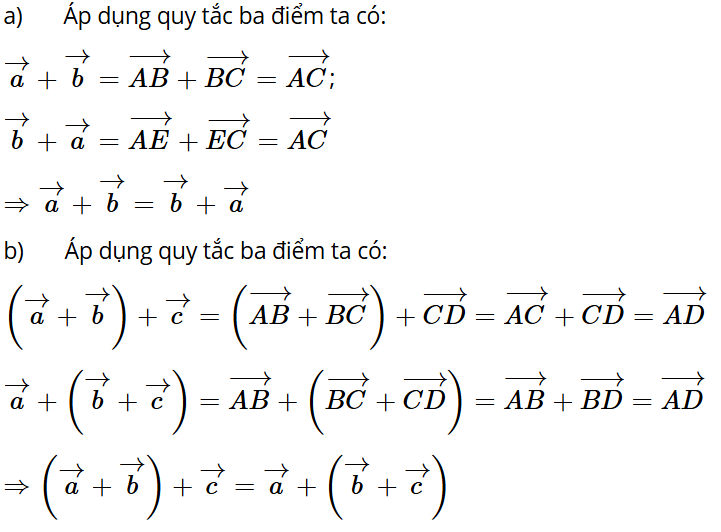
Thực hành 3: Cho hình vuông ABCD có cạnh bằng 1. Tính độ dài của các vectơ sau:

a) $\vec{a} = (\vec{A C} + \vec{B D}) + \vec{C B}$ ;

b) $\vec{a} = \vec{A B} + \vec{A D} + \vec{B C} + \vec{D A}$ .

Trả lời:

Thực hành 3 trang 91 Toán 10 Tập 1 Chân trời sáng tạo | Giải Toán 10

a) Ta có:

$\vec{a} = (\vec{A C} + \vec{B D}) + \vec{C B}$

$= \vec{A C} + \vec{B D} + \vec{C B}$ (bỏ dấu ngoặc)

$= (\vec{A C} + \vec{C B}) + \vec{B D}$ (tính chất giao hoán và kết hợp)

$= \vec{A B} + \vec{B D} = \vec{A D}$ (quy tắc ba điểm)

Do đó $|\vec{a}| = |\vec{A D}| = A D = 1$ .

b) Ta có:

$\vec{a} = \vec{A B} + \vec{A D} + \vec{B C} + \vec{D A}$

$= (\vec{A B} + \vec{B C}) + (\vec{A D} + \vec{D A})$ (tính chất giao hoán và kết hợp)

$= \vec{A C} + \vec{A A}$ (quy tắc ba điểm)

$= \vec{A C} + \vec{0} = \vec{A C}$

Do đó: $|\vec{a}| = |\vec{A C}| = A C$

Xét tam giác ADC vuông tại D, áp dụng định lí Pythagore ta có:

AC2 = AD2 + DC2 = 12 + 12 = 2 $\Rightarrow A C = \sqrt{2}$

Vậy $|\vec{a}| = |\vec{A C}| = A C = \sqrt{2}$ .

3. Hiệu của hai vectơ

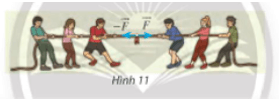
Hoạt động khám phá 3: Tìm hợp lực của hai lực đối nhau $\vec{F}$ và $- \vec{F}$ (Hình 11).

Hoạt động khám phá 3 trang 91 Toán 10 Tập 1 Chân trời sáng tạo | Giải Toán 10

Trả lời:

F⃗ + −F⃗ = 0⃗

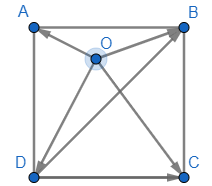
Thực hành 4: Cho hình vuông ABCD có cạnh bằng 1 và một điểm O tùy ý. Tính độ dài của các vectơ sau:

a) $\vec{a} = \vec{O B} - \vec{O D}$ ;

b) $\vec{b} = (\vec{O C} - \vec{O A}) + (\vec{D B} - \vec{D C})$ .

Trả lời:

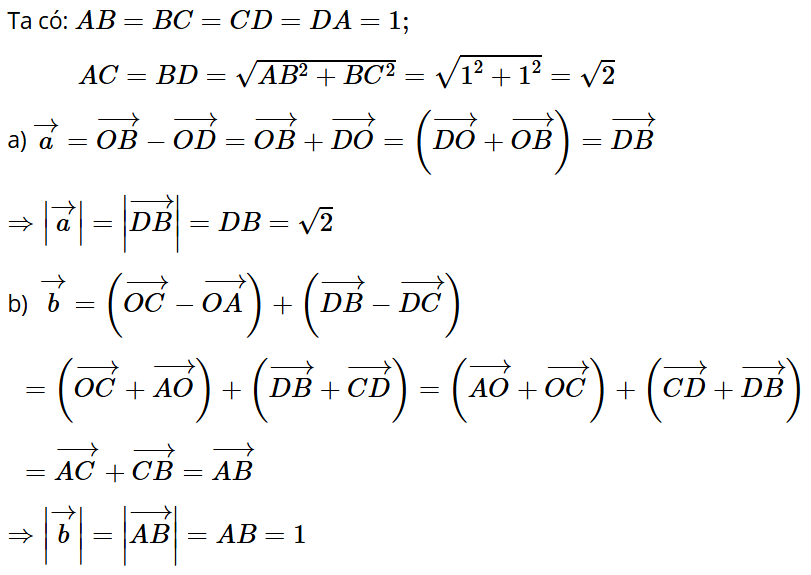
4. Tính chất vectơ của trung điểm đoạn thẳng và trọng tâm tam giác

Hoạt động khám phá 4:

a) Cho điểm M là trung điểm của đoạn thẳng AB. Ta đã biết $\vec{M B} = - \vec{M A} = \vec{A M}$ . Hoàn thành phép cộng vectơ sau: $\vec{M A} + \vec{M B} = \vec{M A} + \vec{A M} = \vec{M M} = ?$

Hoạt động khám phá 4 trang 92 Toán 10 Tập 1 Chân trời sáng tạo | Giải Toán 10

b) Cho điểm G là trọng tâm của tam giác ABC có trung tuyến AI. Lấy D là điểm đối xứng với G qua I. Ta có BGCD là hình bình hành và G là trung điểm của đoạn thẳng AD. Với lưu ý rằng $\vec{G B} + \vec{G C} = \vec{G D}$ và $\vec{G A} = \vec{D G}$ , hoàn thành phép cộng vectơ sau:

$\vec{G A} + \vec{G B} + \vec{G C} = \vec{G A} + \vec{G D} = \vec{D G} + \vec{G D} = \vec{D D} = ?$

Hoạt động khám phá 4 trang 92 Toán 10 Tập 1 Chân trời sáng tạo | Giải Toán 10

Trả lời:

Vectơ có điểm đầu và điểm cuối trùng nhau là vectơ $\vec{0}$ .

Do đó:

a) $\vec{M A} + \vec{M B} = \vec{M A} + \vec{A M} = \vec{M M} = \vec{0}$

b) $\vec{G A} + \vec{G B} + \vec{G C} = \vec{G A} + \vec{G D} = \vec{D G} + \vec{G D} = \vec{D D} = \vec{0}$

Thực hành 5: Cho hình bình hành ABCD có tâm O. Tìm ba điểm M, N, P thỏa mãn:

a) $\vec{M A} + \vec{M D} + \vec{M B} = \vec{0}$ ;

b) $\vec{N D} + \vec{N B} + \vec{N C} = \vec{0}$ ;

c) $\vec{P M} + \vec{P N} = \vec{0}$ .

Trả lời:

a. M là trọng tâm của tam giác ABD;

b. N là trọng tâm của tam giác BCD;

c. P là trung điểm của MN.

Bài tập

Bài tập 1: Cho hình bình hành ABCD có O là giao điểm của hai đường chéo và một điểm M tùy ý. Chứng minh rằng:

a) $\vec{B A} + \vec{D C} = \vec{0}$ ;

b) $\vec{M A} + \vec{M C} = \vec{M B} + \vec{M D}$

Trả lời:

Bài tập 2: Cho tứ giác ABCD, thực hiện các phép cộng và trừ vectơ sau:

a) $\vec{A B} + \vec{B C} + \vec{C D} + \vec{D A}$ ;

b) $\vec{A B} - \vec{A D}$ ;

c) $\vec{C B} - \vec{C D}$ .

Trả lời:

a) Ta có:

$\vec{A B} + \vec{B C} + \vec{C D} + \vec{D A}$

$= (\vec{A B} + \vec{B C}) + (\vec{C D} + \vec{D A})$

$= \vec{A C} + \vec{C A} = \vec{A A} = \vec{0}$

Vậy $\vec{A B} + \vec{B C} + \vec{C D} + \vec{D A} = \vec{0}$ .

b) Ta có: $\vec{A B} - \vec{A D} = \vec{D B}$ .

c) Ta có: $\vec{C B} - \vec{C D} = \vec{D B}$ .

Bài tập 3: Cho tam giác đều ABC cạnh bằng a. Tính độ dài của các vectơ:

a) $\vec{B A} + \vec{A C}$ ;

b) $\vec{A B} + \vec{A C}$ ;

c) $\bar{B A} - \bar{B C}$ .

Trả lời:

a. BA→ + AC→ = BC→

⇒ |BC→| = BC = a

b. Gọi D là điểm đối xứng với A qua BC

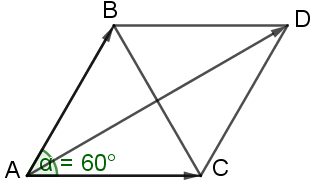
Giải bài 2 Tổng và hiệu của hai vectơ

Ta có: AB→ + AC→ = AD→ (quy tắc hình bình hành)

⇒ |AD→| = AB2+AC2−2AB.AC.cosBADˆ−−−−−−−−−−−−−−−−−−−−−−−−−−√

= a2+a2−2a.a.cos120∘−−−−−−−−−−−−−−−−−−−√ = 3–√a

c. BA→ - BC→ = CA→

⇒ |CA→| = AC = a

Bài tập 4: Cho hình bình hành ABCD có O là giao điểm của hai đường chéo. Chứng minh rằng:

a) $\vec{O A} - \vec{O B} = \vec{O D} - \vec{O C}$ ;

b) $\vec{O A} - \vec{O B} + \vec{D C} = \vec{0}$ .

Trả lời:

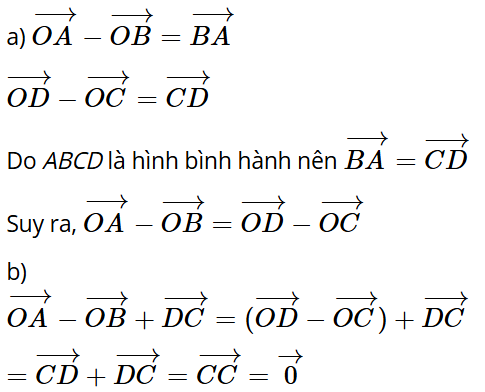
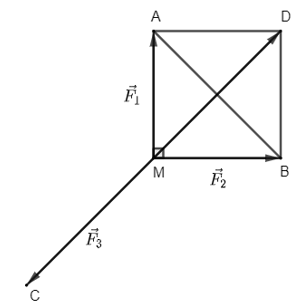
Bài tập 5: Cho ba lực $\vec{F_{1}} = \vec{M A}, \vec{F_{2}} = \vec{M B}$ và $\vec{F_{3}} = \vec{M C}$ cùng tác động vào một vật tại điểm M và vật đứng yên. Cho biết cường độ của $\vec{F_{1}}, \vec{F_{2}}$ đều là 10 N và $\hat{A M B} = 90 °$ . Tìm độ lớn của lực $\vec{F_{3}}$ .

Trả lời:

Bài 5 trang 93 Toán 10 Tập 1 Chân trời sáng tạo | Giải Toán 10

Vì ba lực $\vec{F_{1}}, \vec{F_{2}}, \vec{F_{3}}$ cùng tác động vào vật tại điểm M và vật đứng yên.

Do đó: $\vec{F_{1}} + \vec{F_{2}} + \vec{F_{3}} = \vec{0} \Leftrightarrow \vec{F_{3}} = - (\vec{F_{1}} + \vec{F_{2}})$ (1).

Ta cần tính $\vec{F_{1}} + \vec{F_{2}}$ .

Cường độ của $\vec{F_{1}}$ và $\vec{F_{2}}$ đều là 10 N.

$\Rightarrow |\vec{F_{1}}| = |\vec{F_{2}}| = 10 N .$

Dựng hình bình hành MADB có $\vec{F_{1}} = \vec{M A}, \vec{F_{2}} = \vec{M B}$ và $\hat{A M B} = 90 °$ .

Vì $|\vec{F_{1}}| = |\vec{F_{2}}| = 10 N$ nên MA = MB = 10.

Do đó MADB là hình vuông có cạnh bằng 10.

Suy ra đường chéo MD = $10 \sqrt{2}$ .

Do MADB là hình bình hành nên $\vec{M D} = \vec{M A} + \vec{M B}$ .

$\Rightarrow \vec{M D} = \vec{F_{1}} + \vec{F_{2}}$ (2).
Từ (1) và (2) suy ra: $\vec{F_{3}} = - (\vec{F_{1}} + \vec{F_{2}}) = - \vec{M D}$ .

Vậy lực $\vec{F_{3}}$ có hướng ngược với hướng của $\vec{M D}$ và có độ lớn: $|\vec{F_{3}}| = |\vec{M D}| = 10 \sqrt{2} N .$

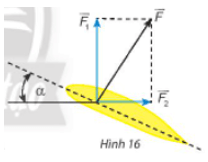
Bài tập 6: Khi máy bay nghiêng cánh một góc α, lực $\vec{F}$ của không khí tác động vuông góc với cánh và bằng tổng của lực nâng $\vec{F_{1}}$ và lực cản $\vec{F_{2}}$ (Hình 16). Cho biết α = 30° và $|\vec{F}| = a$ . Tính $|\vec{F_{1}}|$ và $|\vec{F_{2}}|$ theo a.

Bài 6 trang 93 Toán 10 Tập 1 Chân trời sáng tạo | Giải Toán 10

$|\vec{F_{3}}| = |\vec{M D}| = 10 \sqrt{2} N .$

Trả lời:

Ta có: A2ˆ = α = 30∘ (vì cùng phụ với A1ˆ)

⇒ |F1→| = a.cos30∘ = 3√2a

|F2→| = a.sin30∘ = 12a

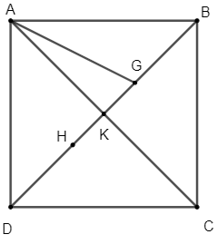
Bài tập 7: Cho hình vuông ABCD có cạnh bằng a và ba điểm G, H, K thỏa mãn: $\vec{K A} + \vec{K C} = \vec{0}; \vec{G A} + \vec{G B} + \vec{G C} = \vec{0}$ ; $\vec{H A} + \vec{H D} + \vec{H C} = \vec{0}$ . Tính độ dài các vectơ $\vec{K A}, \vec{G H}, \vec{A G}$ .

Trả lời:

Bài 7 trang 93 Toán 10 Tập 1 Chân trời sáng tạo | Giải Toán 10

Vì K là điểm thỏa mãn $\vec{K A} + \vec{K C} = \vec{0}$ nên K là trung điểm của AC.

Vì G là điểm thỏa mãn $\vec{G A} + \vec{G B} + \vec{G C} = \vec{0}$ nên G là trọng tâm của tam giác ABC.

Vì H là điểm thỏa mãn $\vec{H A} + \vec{H D} + \vec{H C} = \vec{0}$ nên H là trọng tâm của tam giác ADC.

Do ABCD là hình vuông nên hai đường chéo AC, BD bằng nhau, vuông góc với nhau và cắt nhau tại trung điểm của mỗi đường nên K cũng là trung điểm của BD hay K chính là tâm của hình vuông ABCD.

Trong tam giác ABC, có BK là đường trung tuyến nên G ∈ BK và $G K = \frac{1}{3} B K$ (suy ra từ tính chất trọng tâm tam giác).

Trong tam giác ADC, có DK là đường trung tuyến nên H ∈ DK và $H K = \frac{1}{3} D K$ (suy ra từ tính chất trọng tâm tam giác).

Suy ra H, K, G thẳng hàng và cùng thuộc DB.

Hình vuông ABCD cạnh a nên AC = BD = $a \sqrt{2}$ .

Khi đó: AK = KC = DK = KB = $\frac{1}{2} A C = \frac{1}{2} B D = \frac{a \sqrt{2}}{2}$

Ta có: GH = GK + KH = $\frac{1}{3} B K + \frac{1}{3} D K = \frac{1}{3} . (\frac{a \sqrt{2}}{2} + \frac{a \sqrt{2}}{2}) = \frac{a \sqrt{2}}{3}$

Lại có: $G K = \frac{1}{3} B K = \frac{1}{3} . \frac{a \sqrt{2}}{2} = \frac{a \sqrt{2}}{6}$ .

Xét tam giác AKG vuông tại K (AC ⊥ BD tại K), áp dụng định lí Pythagore ta có:

AG2 = AK2 + KG2 $= {(\frac{a \sqrt{2}}{2})}^{2} + {(\frac{a \sqrt{2}}{6})}^{2} = \frac{5 a}{9}$

Suy ra AG = $\frac{a \sqrt{5}}{3}$ .

Vậy ta tính được độ dài các vectơ $\vec{K A}, \vec{G H}, \vec{A G}$ là:

$\begin{array}{l} |\vec{K A}| = K A = \frac{a \sqrt{2}}{2} \\ |\vec{G H}| = G H = \frac{a \sqrt{2}}{3} \\ |\vec{A G}| = A G = \frac{a \sqrt{5}}{3} \end{array}$

Bài tập 8: Một con tàu có vectơ vận tốc chỉ theo hướng nam, vận tốc của dòng nước là một vectơ theo hướng đông như Hình 17. Tính độ dài vectơ tổng của hai vectơ mói trên.

Bài 8 trang 93 Toán 10 Tập 1 Chân trời sáng tạo | Giải Toán 10

Trả lời: