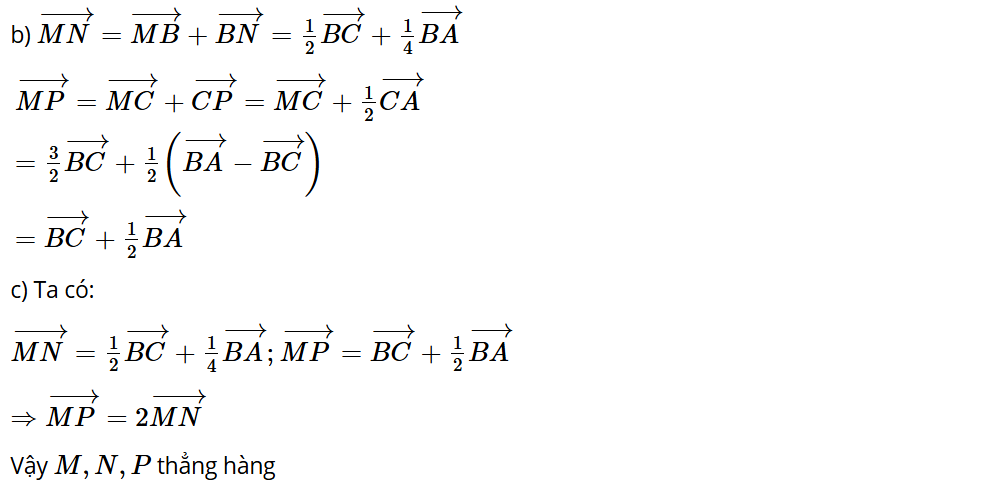Giải SGK Toán 10 Chân trời sáng tạo Bài 3: Tích của một số với một vectơ - Giải SGK Toán 10 - Chân trời sáng tạo

1. Tích của một số với một vectơ và các tính chất

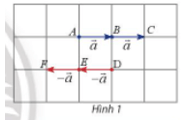
Hoạt động khám phá 1: Cho vectơ $\vec{a}$ . Hãy xác định độ dài và hướng của hai vectơ $\vec{a} + \vec{a}, (- \vec{a}) + (- \vec{a})$ (Hình 1).

Hoạt động khám phá 1 trang 94 Toán 10 Tập 1 Chân trời sáng tạo | Giải Toán 10

Trả lời:

+) Ta có: $A B = |\vec{A B}| = |\vec{a}|$ ; $B C = |\vec{B C}| = |\vec{a}|$

AC = AB + BC = $|\vec{a}| + |\vec{a}| = 2. |\vec{a}|$

Có: $\vec{a} + \vec{a} = \vec{A B} + \vec{B C} = \vec{A C}$

Do đó: $|\vec{a} + \vec{a}| = |\vec{A C}| = A C = 2. |\vec{a}|$

Vậy vectơ $\vec{a} + \vec{a}$ có độ dài là $2. |\vec{a}|$ và có cùng hướng với vectơ $\vec{a}$ (theo hướng đi từ trái qua phải).

+) Ta có: $D E = |\vec{D E}| = |- \vec{a}| = |\vec{a}|$ ; $E F = |\vec{E F}| = |- \vec{a}| = |\vec{a}|$

DF = DE + EF = $|\vec{a}| + |\vec{a}| = 2. |\vec{a}|$

Có: $(- \vec{a}) + (- \vec{a}) = \vec{D E} + \vec{E F} = \vec{D F}$

Do đó: $|(- \vec{a}) + (- \vec{a})| = |\vec{D F}| = D F = 2. |\vec{a}|$

Vậy vectơ $(- \vec{a}) + (- \vec{a})$ có độ dài là $2. |\vec{a}|$ và ngược hướng với vectơ $\vec{a}$ .

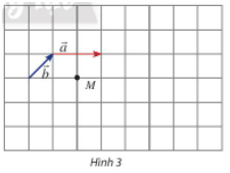
Thực hành 1: Cho hai vectơ $\vec{a}, \vec{b}$ và một điểm M như Hình 3.

Thực hành 1 trang 95 Toán 10 Tập 1 Chân trời sáng tạo | Giải Toán 10

a) Hãy vẽ các vectơ $\vec{M N} = 3 \vec{a}, \vec{M P} = - 3 \vec{b}$ .

b) Cho biết mỗi ô vuông có cạnh bằng 1. Tính: $|3 \vec{b}|, |- 3 \vec{b}|, |2 \vec{a} + 2 \vec{b}|$ .

Trả lời:

Giải bài 3 Tích của một số với một vectơ

b. |3b⃗ | = |-3b⃗ | = 32–√

Giải bài 3 Tích của một số với một vectơ

Ta có: |2a⃗ + 2b⃗ | = 2|a⃗ + b⃗ | = 2|a′→ + b⃗ | = 222+(2–√)2+2.2.2–√.cos45∘−−−−−−−−−−−−−−−−−−−−−−√=10−−√

Thực hành 2: Cho tam giác ABC. Chứng minh G là trọng tâm của tam giác ABC khi và chỉ khi $\vec{M A} + \vec{M B} + \vec{M C} = 3 \vec{M G}$ .

Trả lời:

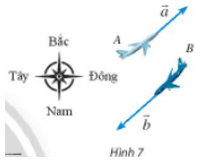
Vận dụng: Một con tàu chở hàng A đang đi về hướng tây với tốc độ 20 hải lí/giờ. Cùng lúc đó, một con tàu chở khách B đang đi về hướng đông với tốc độ 50 hải lí/giờ. Biểu diễn vectơ vận tốc $\vec{b}$ của tàu B theo vectơ vận tốc $\vec{a}$ của tàu A.

Vận dụng trang 95 Toán 10 Tập 1 Chân trời sáng tạo | Giải Toán 10

Trả lời:

Tàu A đi theo hướng từ đông sau tây, tàu B đi theo hướng từ tây sang đông nên hai tàu đi ngược hướng nhau. Do đó vectơ vận tốc của tàu A là $\vec{a}$ và vectơ vận tốc của tàu B là $\vec{b}$ là hai vectơ ngược hướng.

Ta có: $|\vec{a}| = 20$ hải lí/giờ, $|\vec{b}| = 50$ hải lí/giờ.

Suy ra: $\frac{|\vec{b}|}{|\vec{a}|} = \frac{50}{20} = \frac{5}{2} \Rightarrow |\vec{b}| = \frac{5}{2} |\vec{a}|$ .

Vì hai vectơ $\vec{a}$ và $\vec{b}$ ngược hướng và $|\vec{b}| = \frac{5}{2} |\vec{a}|$ .

Do vậy $\vec{b} = - \frac{5}{2} \vec{a}$ .

2. Điều kiện để hai vectơ cùng phương

Hoạt động khám phá 2: Cho hai vectơ $\vec{a}$ và $\vec{b}$ cùng phương, $\vec{b}$ khác $\vec{0}$ và cho $\vec{c} = \frac{|\vec{a}|}{|\vec{b}|} . \vec{b}$ . So sánh độ dài và hướng của hai vectơ $\vec{a}$ và $\vec{c}$ .

Trả lời:

- Hai vectơ a⃗ và c⃗ cùng hướng với nhau.

Thực hành 3: Cho tứ giác ABCD có I và J lần lượt là trung điểm của AB và CD. Cho điểm G thỏa mãn $\vec{G A} + \vec{G B} + \vec{G C} + \vec{G D} = \vec{0}$ . Chứng minh ba điểm I, G, J thẳng hàng.

Trả lời:

Bài tập

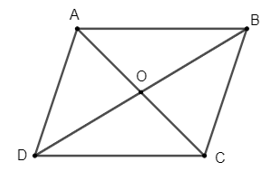
Bài tập 1: Cho hình bình hành ABCD có O là giao điểm hai đường chéo. Với M là điểm tùy ý, chứng minh rằng:

a) $\vec{M A} + \vec{M B} + \vec{M C} + \vec{M D} = 4 \vec{M O}$ ;

b) $\vec{A B} + \vec{A C} + \vec{A D} = 2 \vec{A C}$ .

Trả lời:

Bài 1 trang 97 Toán 10 Tập 1 Chân trời sáng tạo | Giải Toán 10

a) O là giao điểm hai đường chéo của hình bình hành ABCD nên O là trung điểm của AC và BD.

Khi đó: $\vec{O A} + \vec{O C} = \vec{0}, \vec{O B} + \vec{O D} = \vec{0}$

Theo quy tắc ba điểm, ta có: $\vec{M A} + \vec{M B} + \vec{M C} + \vec{M D}$

$= (\vec{M O} + \vec{O A}) + (\vec{M O} + \vec{O B}) + (\vec{M O} + \vec{O C}) + (\vec{M O} + \vec{O D})$

$= 4 \vec{M O} + (\vec{O A} + \vec{O C}) + (\vec{O B} + \vec{O D})$

$= 4 \vec{M O} + \vec{0} + \vec{0} = 4 \vec{M O}$

Vậy $\vec{M A} + \vec{M B} + \vec{M C} + \vec{M D} = 4 \vec{M O}$ .

b) ABCD là hình bình hành nên theo quy tắc hình bình hành ta có: $\vec{A B} + \vec{A D} = \vec{A C}$ .

Khi đó ta có: $\vec{A B} + \vec{A C} + \vec{A D} = (\vec{A B} + \vec{A D}) + \vec{A C} = \vec{A C} + \vec{A C} = 2 \vec{A C}$ .

Vậy $\vec{A B} + \vec{A C} + \vec{A D} = 2 \vec{A C}$ .

Bài tập 2: Cho tứ giác ABCD. Gọi M và N lần lượt là trung điểm của các cạnh AB và CD. Chứng minh rằng:

a) $\vec{A C} + \vec{B D} = 2 \vec{M N}$ ;

b) $\vec{A C} + \vec{B D} = \vec{B C} + \vec{A D}$ .

Trả lời:

a. Ta có: MA→ + MB→ = 0⃗ (M là trung điểm của AB); NC→ + ND→ = 0⃗ (N là trung điểm của CD).

VT = AC→ + BD→ = MC→ - MA→ + MD→ - MB→ = MC→ + MD→ - (MA→ + MB→) = MC→ + MD→ = MN→ + NC→ + MN→ + ND→ = 2MN→ (đpcm)

b. Giả sử: AC→ + BD→ = BC→ + AD→

⇔ AC→ - BC→ = AD→ - BD→

⇔ CB→ - CA→ = DB→ - DA→

⇔ AB→ = AB→ (luôn đúng)

Vậy AC→ + BD→ = BC→ + AD→

Bài tập 3: Cho hai điểm phân biệt A và B. Xác định điểm M sao cho $\vec{M A} + 4 \vec{M B} = \vec{0}$ .

Trả lời:

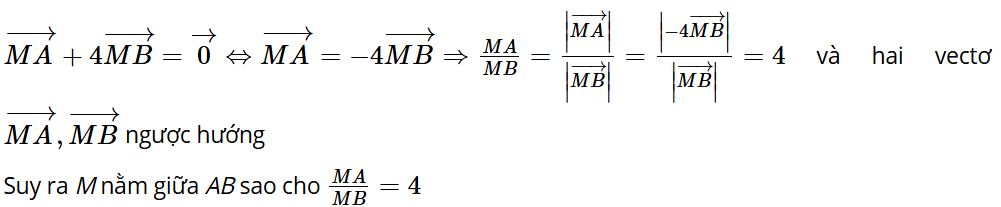
Bài tập 4: Cho tứ giác ABCD. Gọi E, F, G lần lượt là trung điểm của các đoạn thẳng AB, CD, EF. Lấy điểm M tùy ý, chứng minh rằng $\vec{M A} + \vec{M B} + \vec{M C} + \vec{M D} = 4 \vec{M G}$ .

Trả lời:

Vì E là trung điểm của AB nên với điểm G ta có: $\vec{G A} + \vec{G B} = 2 \vec{G E}$ .

Vì F là trung điểm của CD nên với điểm G ta có: $\vec{G C} + \vec{G D} = 2 \vec{G F}$ .

Mà G là trung điểm của EF nên $\vec{G E} + \vec{G F} = \vec{0}$ .

Do đó: $\vec{G A} + \vec{G B} + \vec{G C} + \vec{G D} = 2 \vec{G E} + 2 \vec{G F} = 2 (\vec{G E} + \vec{G F}) = \vec{0}$ .

Với điểm M tùy ý, ta có: $\vec{M A} + \vec{M B} + \vec{M C} + \vec{M D}$

$= (\vec{M G} + \vec{G A}) + (\vec{M G} + \vec{G B}) + (\vec{M G} + \vec{G C}) + (\vec{M G} + \vec{G D})$

$= 4 \vec{M G} + (\vec{G A} + \vec{G B} + \vec{G C} + \vec{G D})$

$= 4 \vec{M G} + \vec{0} = 4 \vec{M G}$

Vậy $\vec{M A} + \vec{M B} + \vec{M C} + \vec{M D} = 4 \vec{M G}$ .

Bài tập 5: Máy bay A đang bay về hướng đông bắc với tốc độ 600 km/h. Cùng lúc đó, máy bay B đang bay về hướng tây nam với tốc độ 800 km/h. Biểu diễn vectơ vận tốc $\vec{b}$ của máy bay B theo vectơ vận tốc $\vec{a}$ của máy bay A.

Bài 5 trang 97 Toán 10 Tập 1 Chân trời sáng tạo | Giải Toán 10

Trả lời:

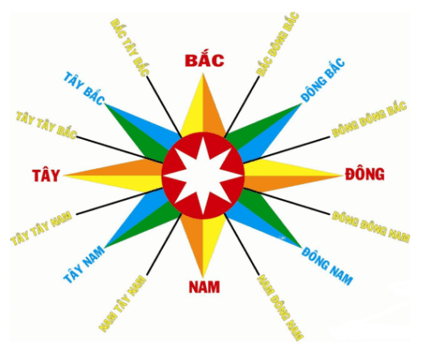
Quan sát bản đồ về hướng sau:

Bài 5 trang 97 Toán 10 Tập 1 Chân trời sáng tạo | Giải Toán 10

Ta thấy hướng đông bắc ngược hướng với hướng tây nam.

Do đó vectơ vận tốc $\vec{b}$ của máy bay B ngược hướng với vectơ vận tốc $\vec{a}$ của máy bay A. (1)

Theo bài ra ta có: $|\vec{a}| = 600$ km/h, $|\vec{b}| = 800$ km/h.

Suy ra: $\frac{|\vec{b}|}{|\vec{a}|} = \frac{800}{600} = \frac{4}{3} \Rightarrow |\vec{b}| = \frac{4}{3} . |\vec{a}|$ (2)

Từ (1) và (2) suy ra: $\vec{b} = - \frac{4}{3} \vec{a}$ .

Bài tập 6: Cho hai điểm phân biệt A và B.

a) Xác định điểm O sao cho $\vec{O A} + 3 \vec{O B} = \vec{0}$ .

b) Chứng minh rằng với mọi điểm M, ta có $\vec{M A} + 3 \vec{M B} = 4 \vec{M O}$ .

Trả lời:

a. O trên đoạn thẳng AB sao cho OA = 3OB

b. Ta có: OA→ + 3OB→ = 0⃗

⇔ MA→ - MO→ + 3(MB→ - MO→) = 0⃗

⇔ MA→ + 3MB→ = 4MO→ (đpcm)

Bài tập 7: Cho tam giác ABC.

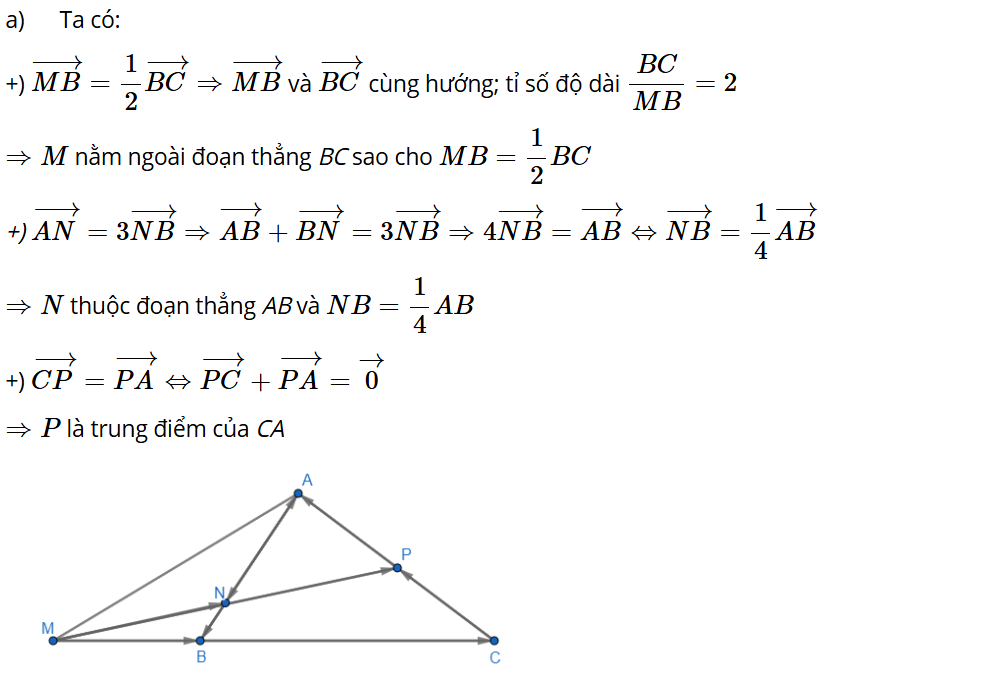
a) Xác định các điểm M, N, P thỏa mãn: $\vec{M B} = \frac{1}{2} \vec{B C}, \vec{A N} = 3 \vec{N B}, \vec{C P} = \vec{P A}$ .

b) Biểu thị mỗi vectơ $\vec{M N}, \vec{M P}$ theo hai vectơ $\vec{B C}, \vec{B A}$ .

c) Chứng minh ba điểm M, N, P thẳng hàng.

Trả lời: