Giải SGK Toán 10 Chân trời sáng tạo Bài 2: Tập hợp

Hoạt động khởi động: Giả sử bạn có một giá sách và các quyển sách như hình dưới đây. Bạn sẽ xếp các quyển sách của mình lên giá như thế nào? Hãy giải thích.

Trả lời:

Gợi ý: Giá sách có 4 ngăn:

+ Ngăn 1 để sách Văn học: Tuyển tập Nam Cao, Dế Mèn phiêu lưu ký, Truyện ngắn chọn lọc, Hoàng Lê nhất thống chí.

+ Ngăn 2 để sách Lịch sử: Lịch sử Việt Nam, Việt Nam sử lược, Lịch sử thế giới.

+ Ngăn 3 để sách Toán học: Lịch sử Toán học, Toán học vui.

+ Ngăn 4 để sách khoa học: Khoa học vui, Vật lí thường thức.

Cách sắp xếp trên dựa vào các thể loại của sách.

1. Nhắc lại về tập hợp

Thực hành 1: 

a) Lấy ba ví dụ về tập hợp và chỉ ra một số phần tử của chúng.

b) Với mỗi tập hợp ℕ, ℤ, ℚ, ℝ hãy sử dụng kí hiệu ∈ và ∉ để chỉ ra hai phần tử thuộc, hai phần tử không thuộc tập hợp đó.

Trả lời:

a) Ba ví dụ về tập hợp:

+) A là tập hợp các bạn học sinh trong tổ 1 của lớp 6A.

Các bạn học sinh trong tổ 1 của lớp 6A là: Hoa, Hùng, Dũng, Lê, Mai, Đạt.

Một phần tử thuộc tập hợp A là Hùng.

+) B là tập hợp các môn thể thao yêu thích của lớp 9B.

Các môn thể thao yêu thích của lớp 9B là: Bóng đá, bóng chuyền, cầu Lông, điền kinh.

Một phần tử thuộc tập hợp B là bóng chuyền.

+) C là tập hợp các nước ở khu vực Đông Nam Á.

Các nước trong khu vực Đông Nam Á là: Việt Nam, Lào, Campuchia, Thái Lan, Myanmar, Malaysia, Singapore, Indonesia, Brunei, Philippines và Đông Timor.

Một phần tử thuộc tập hợp C là Việt Nam.

b)

+) Tập hợp ℕ là tập các số tự nhiên:

Hai phần tử thuộc ℕ là 1; 15. Kí hiệu 1 ∈ ℕ và 15 ∈ ℕ.

Hai phần tử không thuộc ℕ là: -10; 1,2. Kí hiệu – 10 ∉ ℕ và 1,2 ∉ ℕ.

+) Tập hợp ℤ  là tập các số nguyên:

Hai phần tử thuộc ℤ là -200; 1 023. Kí hiệu – 200 ∈ ℤ và 1 023 ∈ ℤ.

Hai phần tử không thuộc ℤ là: $\frac{1}{2};$ - 10,25. Kí hiệu $\frac{1}{2};$ ∉ ℤ và – 10,25 ∉ ℤ.

+) Tập hợp ℚ là tập các số hữu tỉ:

Hai phần tử thuộc ℚ là – 2,7; 1. Kí hiệu – 2,7 ∈ ℚ và 1 ∈ ℚ.

Hai phần tử không thuộc ℚ là:  $\sqrt{2};\pi$. Kí hiệu $\pi$ ∉ ℚ và $\sqrt{2}$ ∉ ℚ.

+) Tập hợp ℝ là tập các số hữu tỉ:

Hai phần tử thuộc ℝ là $-\sqrt{3};\frac{5}{57}$. Kí hiệu $-\sqrt{3}$ ∈ ℝ và $\frac{5}{57}$ ∈ ℝ.

Không có phần tử nào không thuộc tập hợp ℝ.

Thực hành 2: Viết các tập hợp sau đây dưới dạng liệt kê các phần tử và tìm số phần tử của mỗi tập hợp đó:

a) Tập hợp A các ước của 24;

b) Tập hợp B gồm các chữ số trong số 1 113 305;

c) C = {n ∈ ℕ | n là bội của 5 và n ≤ 30};

d) D = {x ∈ ℝ | x2 – 2x + 3 = 0}.

Trả lời:

Thực hành 3: Viết các tập hợp sau đây dưới dạng chỉ ra tính chất đặc trưng cho các phần tử:

a) A = {1; 3; 5; …; 15};

b) B = {0; 5; 10; 15; 20; …};

c) Tập hợp C các nghiệm của bất phương trình 2x + 5 > 0.

Trả lời:

a. A = {x ∈N| x là ước của 15}

b. B = {x ∈N| x là bội của 5}

c. C = {x ∈R| 2x + 5 > 0}

2. Tập con và hai tập hợp bằng nhau

Hoạt động khám phá: Trong mỗi trường hợp sau đây, các phần tử của tập hợp A có thuộc tập hợp B không? Hãy giải thích.

a) A = {-1; 1} và B = {-1; 0; 1; 2};

b) A = ℕ và B = ℤ;

c) A là tập hợp các học sinh nữ của lớp 10E, B là tập hợp các học sinh của lớp này;

d) A là tập hợp các loài động vật có vú, B là tập hợp các loài động vật có xương sống.

Trả lời:

a) Có vì −1 ∈ B, 1 ∈ B

b) Có vì các số tự nhiên cũng là số nguyên.

c) Có vì các học sinh nữ của lớp 10E cũng là học sinh của lớp 10E.

d) Có vì các loài động vật có vú (còn gọi là thú) là một trong các lớp thuộc các loài động vật có xương sống.

Thực hành 4: Trong mỗi cặp tập hợp sau đây, tập hợp nào là tập con của tập hợp còn lại? Chúng có bằng nhau không?

a) A = $\left\{\sqrt{3};-\sqrt{3}\right\}$  và B = {x ∈ ℝ | x2 – 3 = 0};

b) C là tập hợp các tam giác đều và D là tập hợp các tam giác cân;

c) E = {x ∈ ℕ | x là ước của 12} và F = {x ∈ ℕ | x là ước của 24}.

Trả lời:

a) Xét phương trình x2 – 3 = 0 $\iff [\begin{array}{c}x=\sqrt{3}\\ x=-\sqrt{3}\end{array}$

Khi đó B = $\left\{\sqrt{3};-\sqrt{3}\right\}$

Ta thấy các phần tử của tập hợp A đều thuộc tập hợp B nên A ⊂ B.

Ngược lại các phần tử của tập hợp B đều thuộc tập hợp A nên B ⊂ A.

Suy ra A = B.

b) Ta có tam giác đều là tam giác cân.

Suy ra các phần tử của tập hợp C đều thuộc tập hợp D nên C ⊂ D.

Nhưng không phải tất cả tam giác cân đều là tam giác đều. Suy ra không phải tất cả các phần tử của tập hợp D đều thuộc hợp C nên D không là tập con của tập C.

Do đó C ≠ D.

c) Ta có: Ư(12) = {-12; -6; -4; -3; -2; -1; 1; 2; 3; 4; 6; 12}

Khi đó E = {1; 2; 3; 4; 6; 12}.

Ta lại có Ư(24) = {-24; -12; -8; -6; -4; -3; -2; -1; 1; 2; 3; 4; 6; 8; 12; 24}.

Khi đó F = {1; 2; 3; 4; 6; 8; 12; 24}.

Ta thấy các phần tử của tập hợp E thuộc tập hợp F nên E ⊂  F.

Nhưng các phần tử 8; 24 của tập hợp F không thuộc tập hợp E nên F không là tập con của tập E.

Do đó D ≠ E.

Thực hành 5: Viết tất cả các tập con của tập A = {a; b}.

Trả lời:

- Các tập hợp con của A là: M = {a}; N = {b}

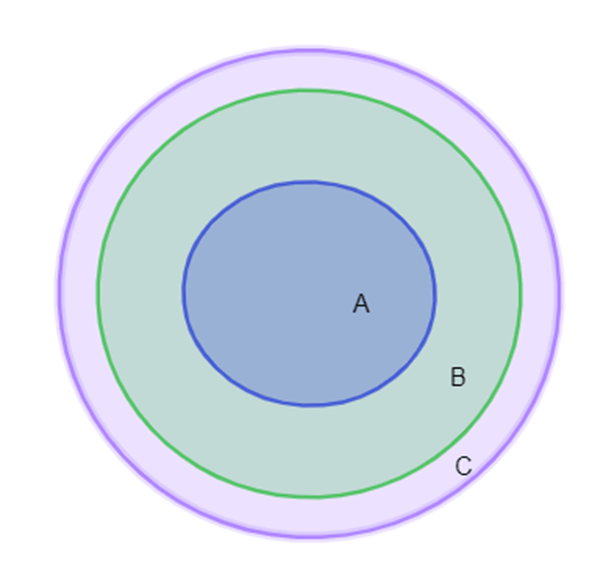
Vận dụng: Bạn An khẳng định rằng: Với các tập hợp A, B, C bất kì, nếu A ⊂ B và B ⊂ C thì A ⊂ C. Khẳng định của bạn An có đúng không? Hãy giải thích bằng cách sử dụng biểu đồ ven.

Trả lời:

Khẳng định của bạn An là đúng.

Thật vậy, ta có sơ đồ ven sau:

Dựa vào sơ đồ ta thấy tập hợp A nằm trong tập hợp B và tập hợp B nằm trong tập hợp C. Do đó tập hợp A nằm hoàn toàn trong tập hợp C hay tất cả phần tử của tập hợp A đều thuộc tập hợp C.

Suy ra A ⊂ C.

3. Một số tập con của tập hợp số thực

Thực hành 6: Dùng các kí hiệu đoạn, khoảng, nửa khoảng để viết các tập hợp sau đây:

a) $\left\{x\in R|-2<x<3\right\};$

b) $\left\{x\in R|1\le x\le 10\right\};$

c) $\left\{x\in R|-5<x\le \sqrt{3}\right\};$

d) $\left\{x\in R|\pi \le x<4\right\};$

e) $\left\{x\in R|x<\frac{1}{4}\right\};$

g) $\left\{x\in R|x\ge \frac{\pi }{2}\right\}.$

Trả lời:

Bài tập

Bài tập 1: Viết các tập hợp sau đây dưới dạng liệt kê các phần tử:

a) A = {x ∈ ℤ| |x| < 5};

b) B = {x ∈ ℝ| 2x2 – x – 1 = 0};

c) C = {x ∈ ℕ | x có hai chữ số}.

Trả lời:

a) A = {x ∈ ℤ | |x| < 5}

Xét |x| < 5

⇔ x < 5 hoặc – x < 5

⇔ x < 5 hoặc x > - 5

Suy ra -5 < x < 5.

Mà x ∈ ℤ nên x ∈ {-4; -3; -2; -1; 0; 1; 2; 3; 4}.

Vậy A = {-4; -3; -2; -1; 0; 1; 2; 3; 4}.

b) Xét phương trình 2x2 – x – 1 = 0

⇔ (x – 1)(2x + 1) = 0

$\iff [\begin{array}{c}x-1=0\\ 2x+1=0\end{array}$

$\iff [\begin{array}{c}x=1\\ x=-\frac{1}{2}\end{array}$

Mà 1; $-\frac{1}{2}$ ∈ ℝ

Vậy B = $\left\{1;-\frac{1}{2}\right\}$

c) Các số tự nhiên có hai chữ số là 10; 11; 12; 13; 14; 15; …; 99.

Vậy C = {10; 11; 12; 13; 14; 15; …; 99}.

Bài tập 2: Viết các tập hợp sau đây dưới dạng chỉ ta tính chất đặc trưng cho các phần tử:

a) Tập hợp A = {1; 2; 3; 6; 9; 18};

b) Tập hợp B các nghiệm của bất phương trình 2x + 1 > 0;

c) Tập hợp C các nghiệm của phương trình 2x – y = 6.

Trả lời:

a. A = {x ∈N | x là ước của 18}

b. B = {x ∈R | 2x + 1 > 0}

c. C = {x ∈R, y ∈R | 2x - y = 6}

Bài tập 3: Trong mỗi cặp tập hợp sau đây, tập hợp nào là tập con của tập còn lại? Chúng có bằng nhau không?

a) A = {x ∈ ℕ | x < 2} và B = {x ∈ ℤ | x2 – x = 0};

b) C là tập hợp các hình thoi và D là tập hợp các hình vuông;

c) E = (-1; 1] và F = $\left(-\infty ;2\right]$

Trả lời:

Bài tập 4: Hãy viết tất cả các tập hợp con của B = {0; 1; 2}.

Trả lời:

Tập con không có phần tử nào: ∅ ;

Tập con có một phần tử: {0}, {1}, {2}.

Tập con có hai phần tử: {0; 1}, {0; 2}, {1; 2}.

Tập con có ba phần tử: {0; 1; 2}.

Vậy tập tất cả các tập hợp con của tập hợp B là: ∅, {0}, {1}, {2}, {0; 1}, {0; 2}, {1; 2}, {0; 1; 2}.

Bài tập 5: Dùng các kí hiệu đoạn, khoảng, nửa khoảng viết các tập hợp sau đây:

a) $\left\{x\in R|-2\pi <x\le 2\pi \right\}$;

b) $\left\{x\in R\left|\right|x|\le \sqrt{3}\right\}$;

c) $\left\{x\in R|x<0\right\}$;

d) $\left\{x\in R|1-3x\le 0\right\}$ .

Trả lời:

a. x ∈ (-2π; 2π]

b. x ∈ [-3–√, 3–√]

c. x ∈ (-∞; 0)

d. x ∈ [13; + ∞)