1. Hình hộp chữ nhật
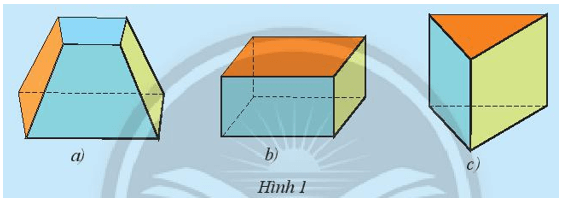
Khám phá 1: Hình nào dưới đây có sáu mặt đều là hình chữ nhật?
Lời giải:
- Hình b là hình có 6 mặt đều là hình chữ nhật.
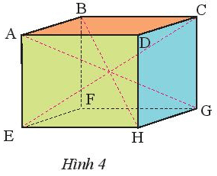
Thực hành 1: Quan sát hình hộp chữ nhật ABCD.EFGH (Hình 4) và thực hiện các yêu cầu sau:
- Nêu các góc ở đỉnh F.
- Nêu các đường chéo được vẽ trong hình.
- Đường chéo chưa được vẽ là đường nào?
Lời giải:
- Các góc ở đỉnh F là: .
- Các đường chéo được vẽ trong hình là: AG, BH, CE.
- Đường chéo chưa được vẽ là: DF.
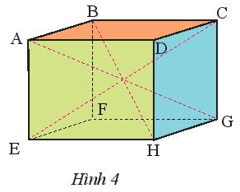
Thực hành 2: Cho hình hộp chữ nhật ABCD.EFGH (Hình 4) có AD = 8 cm, DC = 5 cm, DH = 6,5 cm. Tính độ dài các cạnh AB, FG, AE.
Lời giải:
Ta có:
AB = DC = EF = HG, mà DC = 5 cm nên AB = 5 cm
AD = BC = FG = EH, mà AD = 8 cm nên FG = 8 cm
AE = FB = DH = CG, mà DH = 6,5 cm nên AE = 6,5 cm
2. Hình lập phương
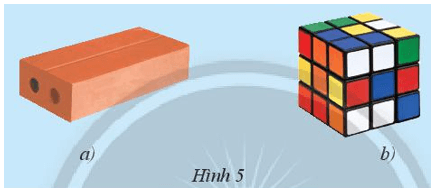
Khám phá 2: Vật nào sau đây có tất cả các mặt đều có dạng hình vuông?
Lời giải:
- Hình 5a) là hình viên gạch có tất cả các mặt đều có dạng hình chữ nhật.
- Hình 5b) là hình khối rubik có tất cả các mặt đều có dạng hình vuông.
Vậy khối rubik có tất cả các mặt đều có dạng hình vuông.
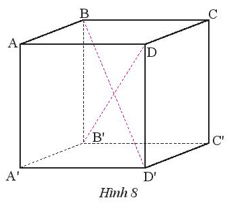
Thực hành 3: Quan sát hình lập phương ABCD.A’B’C’D’ có AB = 5 cm (Hình 8).
- Tìm độ dài các cạnh BC, CC’.
- Nêu các góc ở đỉnh C.
- Nêu các đường chéo chưa được vẽ.
Lời giải:
Vì hình lập phương có tất cả các cạnh bằng nhau, ta có: AB = BC = CD = AD = AA’ = BB’ = CC’ = DD’ = A’B’ = B’C’ = C’D’ = D’A’
Mà AB = 5 cm
=> BC = CC’ = 5cm
+ Các góc ở đỉnh C là: góc BCD, góc BCC’, góc DCC’
+ Các đường chéo chưa được vẽ là: AC’ , A’C
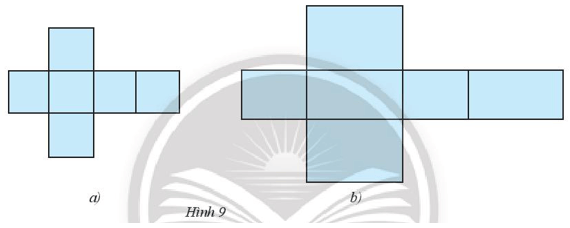
Vận dụng: Trong tấm bìa ở Hình 9, tấm bìa nào gấp được hình hộp chữ nhật, tấm bìa nào gấp được hình lập phương?
Lời giải:
- Hình a gấp được thành hình lập phương
- Hình b gấp được thành hình hộp chữ nhật
Bài tập
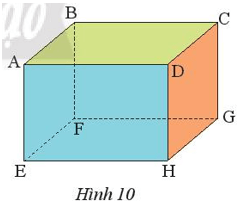
Bài tập 1: Quan sát hình hộp chữ nhật ABCD.EFGH (Hình 10).
a) Nêu các cạnh và đường chéo.
b) Nêu các góc ở đỉnh B và đỉnh C.
c) Kể tên những cạnh bằng nhau.
Lời giải:
Hình hộp chữ nhật ABCD.EFGH có:
a) Các cạnh là: AB, BC, CD, DA, AE, BF, CG, DH, EF, FG, GH, HE.
Các đường chéo là: AG, BH, CE, DF.
b) Các góc ở đỉnh B là: .
Các góc đỉnh C là: .
c) Ta có ABCD.EFGH là hình hộp chữ nhật. Khi đó:
+ ABCD là hình hộp chữ nhật nên AB = CD; BC = AD.
+ ABFE là hình hộp chữ nhật nên AB = EF; AE = BF.
+ BCGF là hình hộp chữ nhật nên BC = GF; BF = CG.
+ ADHE là hình hộp chữ nhật nên AD = EH; AE = DH.
+ CDHG là hình hộp chữ nhật nên CD = GH; DH = CG.
Vậy những cạnh bằng nhau là: AB = CD = EF = GH; BC = AD = GF = EH; AE = BF = CG = DH.
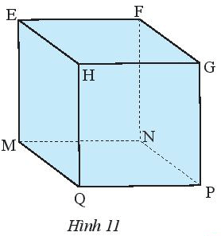
Bài tập 2: Quan sát hình lập phương EFGH.MNPQ (Hình 11).
a) Biết MN = 3 cm. Độ dài các cạnh EF, NF bằng bao nhiêu?
b) Nêu tên các đường chéo của hình lập phương.
Lời giải:
a) Vì hình lập phương có tất cả các cạnh bằng nhau
=> EF = FG = GH = HE = EM = HQ = FN = GP = MN = NP = PQ = QM.
Mà MN = 3 cm
=> EF = NF = 3 cm
b) Các đường chéo của hình lập phương là: EP; FQ; HN; GM.
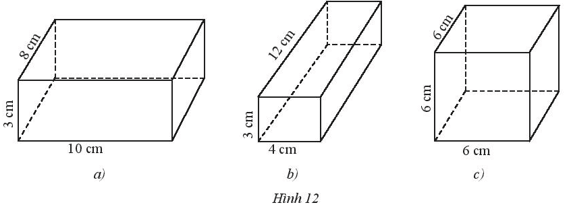
Bài tập 3: Trong các hình dưới đây, hình nào là hình hộp chữ nhật, hình nào là hình lập phương?
Lời giải:
- Hình a, b là hình hộp chữ nhật vì có 6 mặt đều là hình chữ nhật
- Hình c là hình lập phương vì có 6 mặt đều là hình vuông
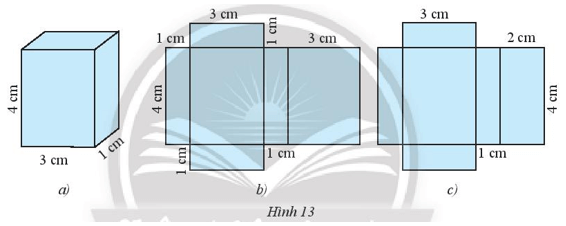
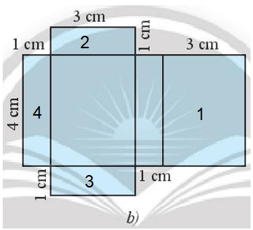
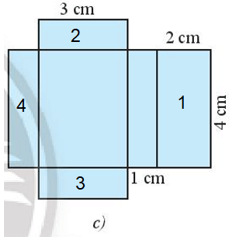
Bài tập 4: Trong hai tấm bìa ở các Hình 13b và Hình 13c, tấm bìa nào có thể gấp được hình hộp chữ nhật ở Hình 13a?
Lời giải:
Hình 13a là hình hộp chữ nhật có chiều dài 3 cm, chiều rộng 1 cm và chiều cao 4 cm.
* Hình 13b:
Khi gấp bìa lại thì:
- Chiều dài của hình chữ nhật 1 trùng với chiều dài của hình chữ nhật 4.
Hình chữ nhật 1 hình chữ nhật 4 là hình nào
- Hai chiều rộng của hình chữ nhật 1 trùng với chiều chiều dài của hai hình chữ nhật 2 và 3.
Do đó, tấm bìa hình 13b có thể gấp được hình hộp chữ nhật ở Hình 13a.
* Hình 13c:
Khi gấp bìa lại thì:
- Chiều dài của hình chữ nhật 1 trùng với chiều dài của hình chữ nhật 4.
- Hai chiều rộng của hình chữ nhật 1 không trùng với chiều chiều dài của hai hình chữ nhật 2 và 3 (chiều rộng của hình chữ nhật 1 là 2 cm, chiều dài của mỗi hình chữ nhật 2 và 3 là 3 cm).
Do đó, tấm bìa hình 13c không thể gấp được hình hộp chữ nhật ở Hình 13a.
Vậy trong hai tấm bìa ở các Hình 13b và Hình 13c, tấm bìa Hình 13b có thể gấp được hình hộp chữ nhật ở Hình 13a.