Giải SGK Toán 7 Chân trời sáng tạo Bài 1: Tập hợp các số hữu tỉ

Khởi động: Phép cộng, phép trừ, phép nhân hai số nguyên có kết quả là một số nguyên. Vậy kết quả của phép chia số nguyên a cho số nguyên b (b ≠ 0) có phải là một số nguyên không?

Lời giải:

Kết quả của một số nguyên a chia cho số nguyên b (b ≠ 0) có thể không là số nguyên.

Ví dụ 3 : 2 = 1,5.

1. Số hữu tỉ

Khám phá 1: Cho các số –7; 0,5; 0; $1\frac{2}{3}$. Với mỗi số, hãy viết một phân số bằng số đã cho.

Lời giải:

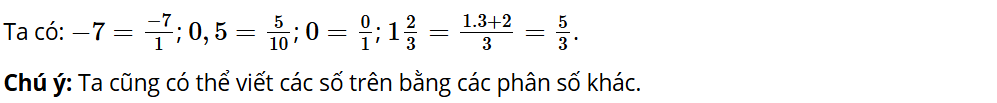
Thực hành 1: Vì sao các số –0,33; 0; $3\frac{1}{2}$; 0,25 là các số hữu tỉ?

Lời giải:

−0,33=−33100

 0=01

312=72

0,25=14

=> Các số -0,33; 0; 312 ; 0,25 là các số hữu tỉ

Vận dụng 1: Viết số đo các đại lượng sau dưới dạng $\frac{a}{b}$ với a, b ∈ ℤ, b ≠ 0.

a) 2,5 kg đường.

b) 3,8 m dưới mực nước biển.

Lời giải:

a) Ta có $2,5=\frac{25}{10}=\frac{5}{2}$ . Vậy 2,5 kg đường bằng $\frac{5}{2}$ kg đường.

b) Vì ta lấy mực nước biển là mốc 0 do đó 3,8 m dưới mực nước biển chính là -3,8 m so với mực nước biển.

Ta có $-3,8=\frac{-38}{10}$ = $\frac{-19}{5}$.

Vậy 3,8 m dưới mực nước biển chính là $\frac{-19}{5}$ m.

2. Thứ tự trong tập hợp các số hữu tỉ

Khám phá 2:

a) So sánh hai phân số $\frac{2}{9}$ và $-\frac{5}{9}$.

b) Trong mỗi trường hợp sau, nhiệt độ nào cao hơn?

i) 0 °C và –0,5 °C;           ii) –12 °C và –7 °C.

Lời giải:

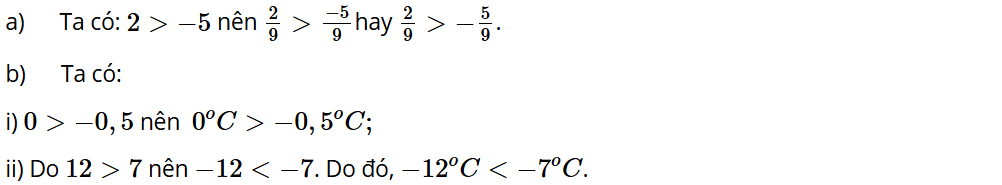
Thực hành 2: Cho các số hữu tỉ: $\frac{-7}{12}$; $\frac{4}{5}$; 5,12; –3; $\frac{0}{-3}$; –3,75.

a) So sánh $\frac{-7}{12}$ với -3,75; $\frac{0}{-3}$ với $\frac{4}{5}$.

b) Trong các số hữu tỉ đã cho, số nào là số hữu tỉ dương, số nào là số hữu tỉ âm, số nào không là số hữu tỉ dương cũng không là số hữu tỉ âm?

Lời giải:

a) • Ta có –3,75 = $\frac{-375}{100}=\frac{\left(-375\right):25}{100:25}=\frac{-15}{4}=\frac{\left(-15\right).3}{4.3}=\frac{-45}{12}$.

Vì -7 > -45 nên $\frac{-7}{12}>\frac{-45}{12}$.

Do đó $\frac{-7}{12}$ > –3,75.

Vậy $\frac{-7}{12}$ > –3,75.

• Ta có $\frac{0}{-3}=0=\frac{0}{5}$.

Vì 0 < 4 nên $\frac{0}{5}<\frac{4}{5}$.

Do đó 0 < $\frac{4}{5}$.

Vậy $\frac{0}{-3}<\frac{4}{5}$.

b) Ta có $\frac{-7}{12}$ < 0; –3,75 < 0; –3 < 0;

$\frac{4}{5}$ > 0; 5,12 > 0; $\frac{0}{-3}$ = 0.

Vậy số hữu tỉ dương là $\frac{4}{5}$ và 5,12; số hữu tỉ âm là $\frac{-7}{12}$ ; –3,75 và –3; số hữu tỉ không âm và cũng không là số hữu tỉ dương là $\frac{0}{-3}$.

3. Biểu diễn số hữu tỉ trên trục số

Khám phá 3:

a) Biễu diễn các số nguyên –1; 1; –2 trên trục số.

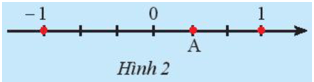
b) Quan sát Hình 2. Hãy dự đoán điểm A biểu diễn số hữu tỉ nào.

Lời giải:

a) Biểu diễn các số nguyên -1; 1; -2 trên trục số:

b) Điểm A biểu diễn số hữu tỉ 13.

Thực hành 3:

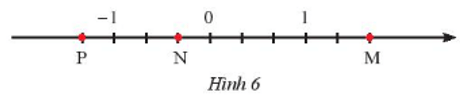
a) Các điểm M, N, P trong Hình 6 biểu diễn các số hữu tỉ nào?

b) Biểu diễn các số hữu tỉ sau trên trục số: –0,75; $\frac{1}{-4}$ ; $1\frac{1}{4}$.

Lời giải:

a)

Ta thấy từ điểm 0 đến điểm 1 và từ điểm –1 đến điểm 0 đều chia thành 3 đoạn bằng nhau, nên đoạn đơn vị mới bằng $\frac{1}{3}$ đoạn đơn vị cũ.

Điểm N nằm bên trái điểm 0 một đoạn bằng 1 đơn vị mới nên điểm N biểu diễn điểm $\frac{-1}{3}$.

Điểm M nằm bên phải điểm 0 một đoạn bằng 5 đơn vị mới nên điểm M biểu diễn điểm $\frac{5}{3}$.

Điểm P nằm bên trái điểm 0 một đoạn bằng 4 đơn vị mới nên điểm P biểu diễn điểm $\frac{-4}{3}$.

b)

• Biểu diễn số hữu tỉ –0,75:

- Ta có –0,75 = $\frac{-75}{100}=\frac{-3}{4}$.

-  Chia đoạn thẳng đơn vị thành bốn phần bằng nhau, ta được đoạn đơn vị mới bằng $\frac{1}{4}$ đơn vị cũ.

- Số hữu tỉ $\frac{-3}{4}$ được biểu diễn bởi điểm A nằm bên trái điểm 0 và cách điểm 0 một đoạn bằng 3 đơn vị mới.

• Biểu diễn số hữu tỉ $\frac{1}{-4}$  

- Ta có $\frac{1}{-4}=\frac{-1}{4}$.

-  Chia đoạn thẳng đơn vị thành bốn phần bằng nhau, ta được đoạn đơn vị mới bằng $\frac{1}{4}$ đơn vị cũ.

- Số hữu tỉ $\frac{-1}{4}$ được biểu diễn bởi điểm B nằm bên trái điểm 0 và cách điểm 0 một đoạn bằng 1 đơn vị mới.

• Biểu diễn số $1\frac{1}{4}$

-  Ta có $1\frac{1}{4}=\frac{1.4+1}{4}=\frac{5}{4}$.

-  Chia đoạn thẳng đơn vị thành bốn phần bằng nhau, ta được đoạn đơn vị mới bằng $\frac{1}{4}$ đơn vị cũ.

- Số hữu tỉ $\frac{5}{4}$ được biểu diễn bởi điểm C nằm bên phải điểm 0 và cách điểm 0 một đoạn bằng 5 đơn vị mới.

4. Số đối của một số hữu tỉ

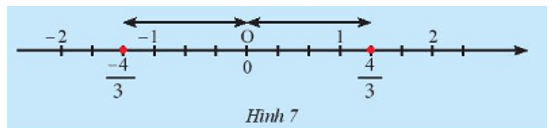
Khám phá 4: Em có nhận xét gì về vị trí điểm $\frac{-4}{3}$ và $\frac{4}{3}$ trên trục số (Hình 7) so với điểm 0?

Lời giải:

Thực hành 4: Tìm số đối của của mỗi số sau: 7; $\frac{-5}{9}$; –0,75; 0; $1\frac{2}{3}$.

Lời giải:

- Số đối của các số: 7; −59; -0,75; 123 lần lượt là: -7; 59; 0,75; −123

Vận dụng 2: Bạn Hồng đã phát biểu: “4,1 lớn hơn 3,5. Vì thế –4,1 cũng lớn hơn –3,5”.

Theo em, phát biểu của bạn Hồng có đúng không? Tại sao?

Lời giải:

Ta có –4,1 = $\frac{-41}{10}$ và –3,5 = $\frac{-35}{10}$.

Mà –41 < –35 nên $\frac{-41}{10}$ < $\frac{-35}{10}$.

Do đó –4,1 < –3,5.

Vậy phát biểu của bạn Hồng không đúng.

Bài tập

Bài tập 1: Thay  bằng kí kiệu ∈, ∉ thích hợp.

-7  ℕ;                  -17  ℤ;;                -38  ℚ;

$\frac{4}{5}$  ℤ;                  $\frac{4}{5}$  ℚ;               0,25  ℤ;               3,25  ℚ

Lời giải:

Ta có – 7 là một số nguyên âm nên –7 không thuộc ℕ, ta viết: -7 $\notin$ ℕ;

Ta có –17 là một số nguyên âm nên –17 thuộc ℤ, ta viết: -17 $\in$ ℤ;

Ta có -38 = $\frac{-38}{1}$, trong đó 1 ∈ ℤ và 1 ≠ 0 nên -38 $\in$ ℚ

Ta có 4; 5 ∈ ℤ và 5 ≠ 0 nên $\frac{4}{5}$ là một số hữu tỉ và không là một số nguyên, do đó ta viết $\frac{4}{5}\notin Z$ và $\frac{4}{5}\in Q$;

Ta có 0,25 không là một số nguyên nên 0,25 $\notin$ ℤ;

Ta có 3,25 = $\frac{325}{100}=\frac{13}{4}$, trong đó 13; 4 ∈ ℤ và 4 ≠ 0, do đó 3,25 $\in$ ℚ.

Bài tập 2:

a) Trong các phân số sau, những phân số nào biểu diễn số hữu tỉ $\frac{-5}{9}$ ?

$\frac{-10}{18};\frac{10}{18};\frac{15}{-27};-\frac{20}{36};\frac{-25}{27}$.

b) Tìm số đối của mỗi số sau: 12; $\frac{4}{9}$; -0,375; $\frac{0}{5}$; -$2\frac{2}{5}$.

Lời giải:

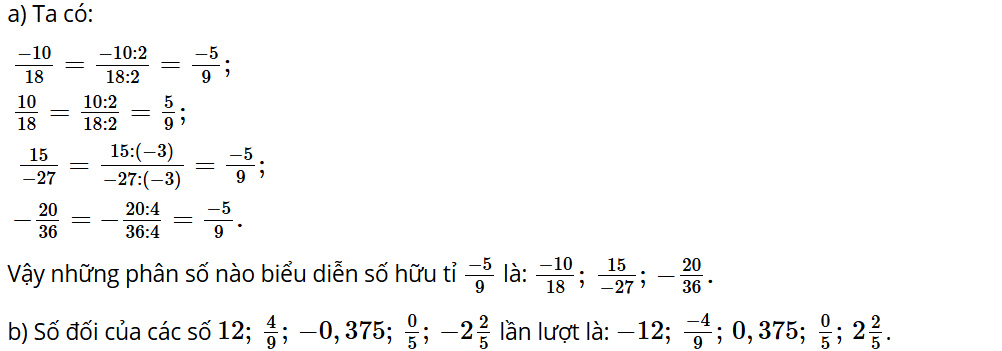
Bài tập 3:

a) Bài 3 trang 9 Toán 7 Tập 1 Chân trời sáng tạo?

b) Biểu diễn các số hữu tỉ $\frac{-2}{5};1\frac{1}{5};\frac{3}{5};-0,8$ trên trục số.

Lời giải:

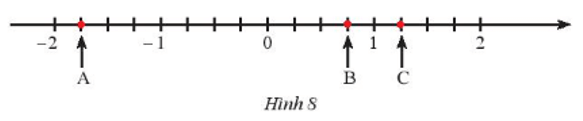
a)  Các điểm A, B, C trong hình 8 lần lượt biểu diễn các số hữu tỉ: −74; 34; 54

b) Biểu diễn các số hữu tỉ −25; 115 ; 35 ; -0,8 :

Bài tập 4:

a) Trong các số hữu tỉ sau, số nào là số hữu tỉ dương, số nào là số hữu tỉ âm, số nào không là số hữu tỉ dương cũng không là số hữu tỉ âm?

$\frac{5}{12};-\frac{4}{5};2\frac{2}{3};-2;\frac{0}{234};-0,32$.

b) Hãy sắp xếp các số trên theo thứ tự từ nhỏ đến lớn.

Lời giải:

a) Ta có:

$\frac{5}{12}$ > 0;

$2\frac{2}{3}$ > 0;

$\frac{-4}{5}$ < 0;

-2 < 0;

-0,32 < 0;

$\frac{0}{234}$ = 0.

Vậy số hữu tỉ dương là $\frac{5}{12}$ và $2\frac{2}{3}$; số hữu tỉ âm là $-\frac{4}{5}$; –0,32 và –2; số không phải là số hữu tỉ dương cũng không phải là số hữu tỉ âm là $\frac{0}{234}$.

b) Ta chia các số hữu tỉ đã cho thành ba nhóm:

Nhóm 1: Gồm các số hữu tỉ âm: $-\frac{4}{5}$; –0,32; –2.

Nhóm 2: Gồm các số hữu tỉ dương $\frac{5}{12}$ và $2\frac{2}{3}$.

Nhóm 3: Số không là số hữu tỉ dương cũng không là số hữu tỉ âm: $\frac{0}{234}$.

So sánh nhóm 1:

Ta có $\frac{-4}{5}=\frac{-20}{25}$; -2 = $\frac{-50}{25}$; -0,32 = $\frac{-32}{100}=\frac{-8}{25}$.

Vì –50 < –20 < –8 nên $\frac{-50}{25}<\frac{-20}{25}<\frac{-8}{25}$. 

Do đó –2 < $\frac{-4}{5}$ < –0,32.

So sánh nhóm 2:

Ta có $2\frac{2}{3}=\frac{2.3+2}{3}=\frac{8}{3}=\frac{32}{12}$.

Do đó $\frac{5}{12}<2\frac{2}{3}$.

Xét nhóm 3 có $\frac{0}{234}$ = 0.

Vì số hữu tỉ âm luôn bé hơn 0 và bé hơn số hữu tỉ dương nên ta có:

–2 < $\frac{-4}{5}$ < –0,32 < $\frac{0}{234}$ < $\frac{5}{12}<2\frac{2}{3}$

Vậy sắp xếp các số theo thứ tự từ nhỏ đến lớn là: -2; $\frac{-4}{5}$; -0,32; $\frac{0}{234}$; $\frac{5}{12}$; $2\frac{2}{3}$

Bài tập 5: So sánh các cặp số hữu tỉ sau:

a) $\frac{2}{-5}$ và $\frac{-3}{8}$;

b) -0,85 và $\frac{-17}{20}$;

c) $\frac{-137}{200}$ và $\frac{37}{-25}$;

d) $-1\frac{3}{10}$ và $-\left(\frac{-13}{-10}\right)$.

Lời giải:

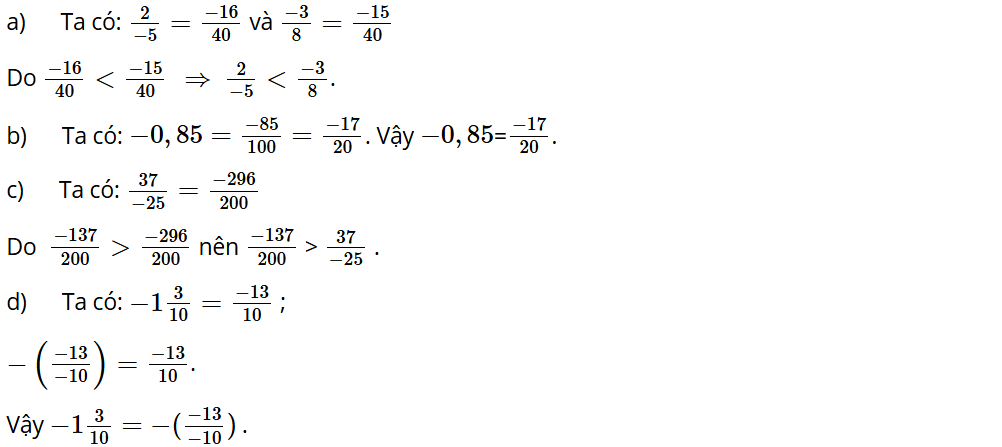
Bài tập 6: So sánh các cặp số hữu tỉ sau:

a) $\frac{-2}{3}$ và $\frac{1}{200}$;

b) $\frac{139}{138}$ và $\frac{1375}{1376}$;

c) $\frac{-11}{33}$ và $\frac{25}{-76}$.

Lời giải:

a) Ta có $\frac{-2}{3}$ < 0 và 0 < $\frac{1}{200}$.

Vậy $\frac{-2}{3}$ < $\frac{1}{200}$.

b) Ta có

$\frac{139}{138}=\frac{138+1}{138}=\frac{138}{138}+\frac{1}{138}$ = 1 + $\frac{1}{138}$ > 1;

$\frac{1375}{1376}=\frac{1376-1}{1376}=\frac{1376}{1376}-\frac{1}{1376}$ = 1 - $\frac{1}{1376}$ < 1.

Vậy $\frac{139}{138}$ > $\frac{1375}{1376}$.

c) Ta có $\frac{-11}{33}=\frac{-1}{3}=\frac{-25}{75}$

Vì 75 < 76 nên $\frac{-25}{75}<\frac{-25}{76}$.

Vậy $\frac{-11}{33}$ < $\frac{25}{-76}$.

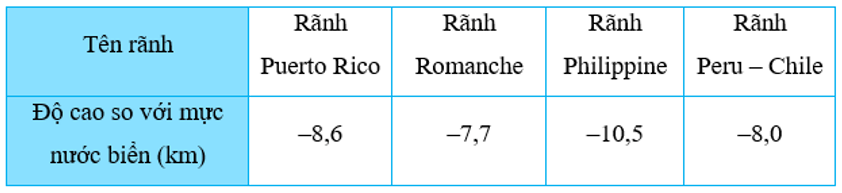
Bài tập 7: Bảng dưới đây cho biết độ cao của bốn rãnh đại dương so với mực nước biển.

(Theo: https://vi.wikipedia.org/wiki/Rãnh_đại_dương)

a) Những rãnh đại dương nào có độ cao cao hơn rãnh Puerto Rico? Giải thích.

b) Rãnh đại dương nào có độ cao thấp nhất trong bốn rãnh trên? Giải thích.

Lời giải:

Bảng dưới đây cho biết độ cao của bốn rãnh đại dương so với mực nước biển.

a) Có : -10,5 < -8,6 < -8,0 < -7,7

Vậy rãnh Philippine có độ cao cao hơn rãnh Peurto Rico

b) Có : -7,7 > -8,0 > -8,6 > -10,5

Vậy rãnh Romanche có độ cao thấp nhất trong bốn rãnh trên.