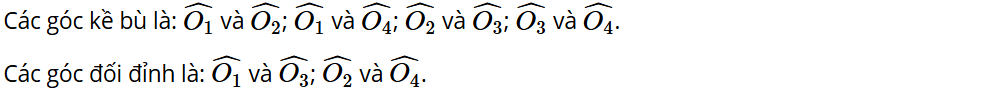Giải SGK Toán 7 Chân trời sáng tạo Bài tập cuối chương IV

Bài tập 1: Trong những câu sau, em hãy chọn những câu đúng.

Tia Oz là tia phân giác của góc ${\mathrm{xOy^\backslash widehat\{xOy\}xOy}}^{}$ khi:

a) ${\mathrm{xOz^\backslash widehat\{xOz\}xOz}}^{}={\mathrm{yOz^\backslash widehat\{yOz\}yOz}}^{}$.

b) ${\mathrm{xOz^\backslash widehat\{xOz\}xOz}}^{}+{\mathrm{zOy^\backslash widehat\{zOy\}zOy}}^{}={\mathrm{xOy^\backslash widehat\{xOy\}xOy}}^{}$.

c) ${\mathrm{xOz^\backslash widehat\{xOz\}xOz}}^{}={\mathrm{yOz^\backslash widehat\{yOz\}yOz}}^{}=\frac{\widehat{xOy}}{2}$.

Lời giải:

Chọn C

Giải thích:

Vì tia Oz là tia phân giác của góc ${\mathrm{xOy^\backslash widehat\{xOy\}xOy}}^{}$ nên:

+ Tia Oz nằm giữa hai tia Ox và Oy: ${\mathrm{xOz^\backslash widehat\{xOz\}xOz}}^{}+{\mathrm{zOy^\backslash widehat\{zOy\}zOy}}^{}={\mathrm{zOy^\backslash widehat\{zOy\}xOy}}^{}$ (1).

+$xOz^\backslash widehat\{xOz\}xOz={\mathrm{yOz^\backslash widehat\{yOz\}yOz}}^{}$ (2).

Từ (1) và (2) suy ra: ${\mathrm{xOz^\backslash widehat\{xOz\}xOz}}^{}={\mathrm{zOy^\backslash widehat\{zOy\}zOy}}^{}=\frac{\widehat{xOy}}{2}$.

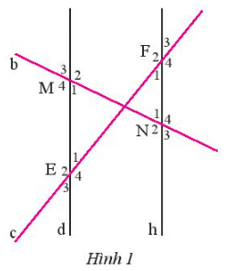
Bài tập 2: Quan sát Hình 1, biết d // h. Hãy kể tên một số cặp góc bằng nhau có trong Hình 1.

Lời giải:

M1ˆ=M3ˆ ; M2ˆ=M4ˆ (các cặp  góc đối đỉnh)

N1ˆ=N3ˆ ; N2ˆ=N4ˆ (các cặp  góc đối đỉnh)

E1ˆ=E3ˆ ; E2ˆ=E4ˆ (các cặp  góc đối đỉnh)

F1ˆ=F3ˆ ; F2ˆ=F4ˆ (các cặp  góc đối đỉnh)

 Vì d // h 

=> M1ˆ=N1ˆ ; M2ˆ=N2ˆ ; E1ˆ=F1ˆ; E4ˆ=F2ˆ(các cặp góc so le trong)

M1ˆ=N3ˆ ; M4ˆ=N2ˆ ; M3ˆ=N1ˆ ; M2ˆ=N4ˆ (các cặp góc đồng vị)

E1ˆ=F3ˆ ; E2ˆ=F2ˆ;  E3ˆ=F1ˆ; E4ˆ=F4ˆ;(các cặp góc đồng vị)

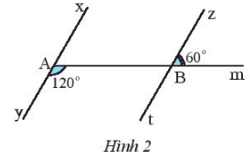
Bài tập 3: Quan sát Hình 2. Chứng minh rằng xy // zt.

Lời giải:

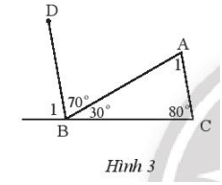
Bài tập 4: Quan sát Hình 3.

a) Tính ${\hat{B}}_1$.

b) Chứng minh rằng AC // BD.

c) Tính ${\hat{A}}_1$.

Lời giải:

a) Ta có ${\mathrm{CBD^\backslash widehat\{CBD\}CBD}}^{}={\mathrm{CBA^\backslash widehat\{CBA\}CBA}}^{}+$$\widehat{CBA}$.

Suy ra ${\mathrm{CBD^\backslash widehat\{CBD\}CBD}}^{}={30}^o+{70}^o={100}^o$.

Vì ${\mathrm{CBD^\backslash widehat\{CBD\}CBD}}^{}$ và ${\hat{B}}_1$ là hai góc kề bù nên:

${\mathrm{CBD^\backslash widehat\{CBD\}CBD}}^{}+{\hat{B}}_1={180}^o$

${100}^o+{\hat{B}}_1={180}^o$

Suy ra: ${\hat{B}}_1={180}^o-{100}^o={80}^o$.

Vậy ${\hat{B}}_1={80}^o$.

b) Ta có ${\mathrm{CBA^\backslash widehat\{CBA\}CAB}}^{}={\hat{B}}_1={80}^o$.

Mà ${\mathrm{CBA^\backslash widehat\{CBA\}CBD}}^{}$ và ${\hat{B}}_1$ là hai góc đồng vị nên AC // BD..

Vậy AC // BD.

c) Vì AC // BD nên ${\hat{A}}_1={\mathrm{CBA^\backslash widehat\{CBA\}ABD}}^{}={70}^o$ (hai góc so le trong)

Vậy ${\hat{A}}_1={70}^o$.

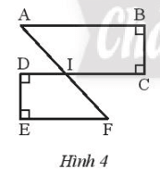
Bài tập 5: Quan sát Hình 4. Chứng minh rằng:

a) AB // CD và EF // CD.

b) AB // EF.

Lời giải:

a) AB⊥BC;CD⊥BC⇒AB//CD ( Từ vuông góc đến song song)

EF⊥DE;CD⊥DE⇒EF//CD ( Từ vuông góc đến song song)

b) Vì AB // CD ; EF // CD => AB // EF 

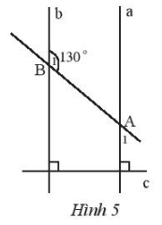
Bài tập 6: Cho Hình 5 có ${\hat{B}}_1={130}^o$. Số đo của ${\hat{A}}_1$ là bao nhiêu?

Lời giải:

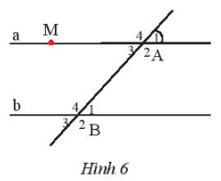
Bài tập 7: Cho Hình 6, biết hai đường thẳng a và b song song với nhau và ${\hat{A}}_1={50}^o$.

a) Hãy viết tên các cặp góc so le trong và các cặp góc đồng vị.

b) Tính số đo của ${\hat{A}}_3,{\hat{B}}_3$.

c) Kẻ đường thẳng c vuông góc với đường thẳng a tại M. Chứng minh rằng c ⊥ b.

Lời giải:

a) Các cặp góc so le trong là: ${\hat{A}}_2$ và ${\hat{B}}_4$; ${\hat{A}}_3$ và ${\hat{B}}_1$.

Các cặp góc đồng vị là: ${\hat{A}}_1$ và ${\hat{B}}_1$; ${\hat{A}}_2$ và ${\hat{B}}_2$; ${\hat{A}}_3$ và ${\hat{B}}_3$; ${\hat{A}}_4$ và ${\hat{B}}_4$ .

b) Ta có: ${\hat{A}}_1={\hat{A}}_3={50}^o$ (hai góc đối đỉnh).

Vì a // b nên ${\hat{A}}_3={\hat{B}}_3={50}^o$ (hai góc đồng vị).

Vậy ${\hat{A}}_3={50}^o,{\hat{B}}_3={50}^o$.

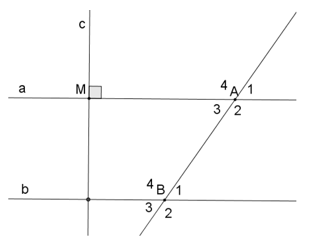
c) Vẽ đường thẳng c vuông góc với đường thẳng a tại M.

Ta có hình vẽ:

Vì a // b và a ⊥ c nên c ⊥ b.

Vậy c ⊥ b.

Bài tập 8: Vẽ đường thẳng m song song với đường thẳng n. Vẽ đường thẳng d cắt đường thẳng m tại điểm I.

a) Hỏi nếu d // n thì điều này có trái với tiên đề Euclid không?

b) Sử dụng kết quả của câu a để chứng minh d cắt n.

Lời giải:

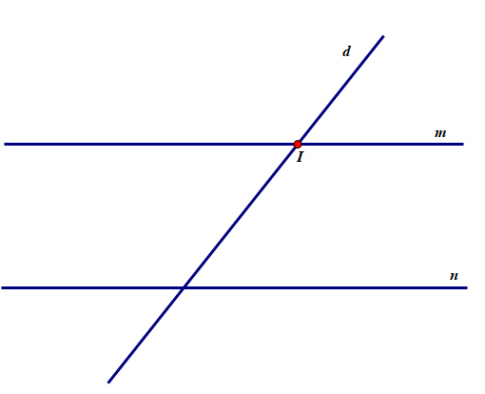
a) Nếu d // n thì qua điểm I nằm ngoài đường thẳng n, có 2 đường thẳng là m và d song song với n ( Trái với tiên đề Euclid)

b) Vì d không thể song song với n (câu a) và d khác n nên d cắt n.

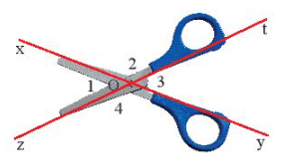
Bài tập 9: Qua điểm O là chốt xoay của một cái kéo, kẻ hai đường thẳng xOy và zOt lần lượt song song với hai lưỡi kéo (Hình 7). Tìm các góc kề bù và các góc đối đỉnh có trong hình vừa vẽ.

Lời giải: