Giải SGK Toán 8 Cánh Diều Bài 1: Đơn thức nhiều biến. Đa thức nhiều biến

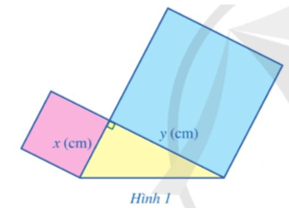
Khởi động: Trong giờ học Mĩ thuật, bạn Hạnh dán lên trang vở hai hình vuông và một tam giác vuông có độ dài hai cạnh hình vuông và một tam giác vuông có độ dài hai cạnh góc vuông là x (cm), y (cm) như Hình 1.

Tổng diện tích của hai hình vuông và tam giác vuông là:

$x^2+y^2+\frac{1}{2}xy$ (cm2).

Biểu thức đại số $x^2+y^2+\frac{1}{2}xy$ còn được gọi là gì?

Trả lời:

- Biểu thức đại số $x^2+y^2+\frac{1}{2}xy$ còn được gọi đa thức nhiều biến.

I. Đơn thức nhiều biến

Hoạt động 1:

a) Viết biểu thức biểu thị:

- Diện tích của hình vuông có độ dài cạnh là x (cm);

- Diện tích của hình chữ nhật có độ dài hai cạnh lần lượt là 2x (cm), 3y (cm);

- Thể tích của hình hộp chữ nhật có ba kích thước lần lượt là x (cm), 2y (cm), 3z (cm).

b) Cho biết mỗi biểu thức trên gồm những số, biến và phép tính nào.

Trả lời:

Luyện tập, vận dụng 1: Trong những biểu thức sau, biểu thức nào là đơn thức?

5y; y+3z; $\frac{1}{2}{x}^3{y}^2{x}^{2}z$

Trả lời:

Trong các biểu thức đó, biểu thức là đơn thức sẽ là: 5y; 12x3y2x2z

Hoạt động 2: Xét đơn thức 2x3y4. Trong đơn thức này, các biến x, y được viết bao nhiêu lần dưới dạng một lũy thừa với số mũ nguyên dương?

Trả lời:

Trong đơn thức 2x3y4

• Biến x được viết một lần dưới dạng một lũy thừa với số mũ nguyên dương là 3.

• Biến y được viết một lần dưới dạng một lũy thừa với số mũ nguyên dương là 4.

Luyện tập, vận dụng 2: Thu gọn mỗi đơn thức sau:

$y^3{y}^{2}z;\frac{1}{3}x{y}^2{x}^{3}z$

Trả lời:

Thu gọn mỗi đơn thức:

y3y2z = y5z;

13x4y2z

Hoạt động 3: Cho hai đơn thức: 2x3y4 và −3x3y4.

a) Nêu hệ số của mỗi đơn thức trên.

b) So sánh phần biến của hai đơn thức trên.

Trả lời:

Luyện tập, vận dụng 3: Các đơn thức trong mỗi trường hợp sau có đồng dạng hay không? Vì sao?

a) x2y4; −3x2y4 và $\sqrt{5}{x}^2{y}^4$.

b) −x2y2z2 và −2x2y2z3.

Trả lời:

a) Các đơn thức x2y4; −3x2y4 và $\sqrt{5}{x}^2{y}^4$ có cùng phần biến là x2y4.

Do đó, các đơn thức x2y4; −3x2y4 và $\sqrt{5}{x}^2{y}^4$ đồng dạng.

b) Đơn thức −x2y2z2 có phần biến là x2y2z2 và đơn thức −2x2y2z3 có phần biến là x2y2z3.

Vì hai đơn thức −x2y2z2 và −2x2y2z3 có phần biến khác nhau nên hai đơn thức này không đồng dạng.

Hoạt động 4:

a) Tính tổng: 5x3 + 8x3.

b) Tính hiệu: 10y7 − 15y7.

Trả lời:

a. Tính tổng: 5x3 + 8x3 = (5+8) x3 = 13x3

b. Tính hiệu: 10y7 - 15y7 =(10-15)y7 = - 5y7

Luyện tập, vận dụng 4: Thực hiện phép tính:

a) 4x4y6 + 2x4y6;

b) 3x3y5 – 5x3y5.

Trả lời:

a. 4x4y6 + 2x4y6= (4+2) x4y6 = 6x4y6 

b. 3x3y5 - 5x3y5 = (3-5) x3y5 = -2x3y5

II. Đa thức nhiều biến

Hoạt động 5: Cho biểu thức x2 + 2xy + y2.

a) Biểu thức trên có bao nhiêu biến?

b) Mỗi số hạng xuất hiện trong biểu thức có dạng như thế nào?

Trả lời:

a) Biểu thức x2 + 2xy + y2 có hai biến x, y.

b) Mỗi số hạng xuất hiện trong biểu thức là các đơn thức (lũy thừa, tích giữa số và các biến).

Luyện tập, vận dụng 5: Trong những biểu thức sau, biểu thức nào là đa thức?

$y+3z+\frac{1}{2}{y}^{2}z;\frac{x^2+y^2}{x+y}$

Trả lời:

Biểu thức: y+3z+12y2z là một đa thức.

Hoạt động 6: Cho đa thức: P = x3 + 2x2y + x2y + 3xy2 + y3.

Thực hiện phép cộng các đơn thức đồng dạng sao cho trong đa thức P không còn hai đơn thức nào đồng dạng.

Trả lời:

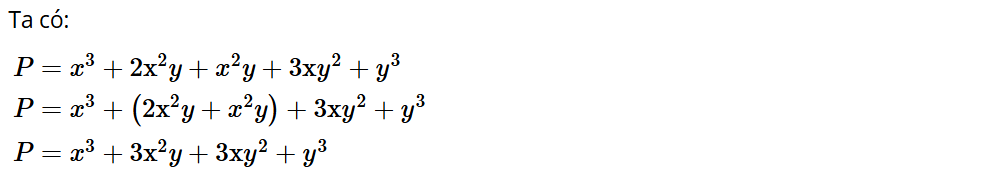
Luyện tập, vận dụng 6: Thu gọn đa thức:

R = x3 – 2x2y – x2y + 3xy2 – y3.

Trả lời:

Ta có R = x3 – 2x2y – x2y + 3xy2 – y3

= x3 – (2x2y + x2y) + 3xy2 – y3

= x3 – 3x2y + 3xy2 – y3.

Hoạt động 7: Cho đa thức: P = x2 – y2. Đa thức P được xác định bằng biểu thức nào? Tính giá trị của P tại x = 1; y = 1.

Trả lời:

Đa thức P được xác định bằng biểu thức: x2−y2.

Tại x= 1; y= 1, giá trị của P là: P = 12−12 = 0.

Luyện tập, vận dụng 7: Tính giá trị của đa thức

Q = x3 – 3x2y + 3xy2 – y3 tại x = 2; y = 1.

Trả lời:

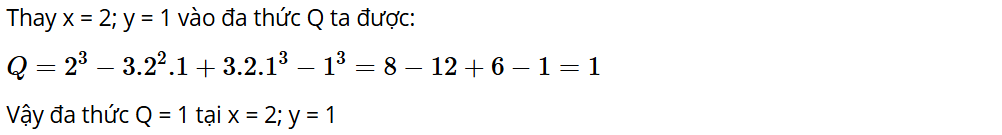
Bài tập

Bài tập 1:

a) Trong những biểu thức sau, biểu thức nào là đơn thức?

$\frac{1}{5}x{y}^2{z}^3;3-2x^3{y}^{2}z;-\frac{3}{2}{x}^{4}yx{z}^2;\frac{1}{2}{x}^2(y^3-z^3).$

b) Trong những biểu thức sau, biểu thức nào là đa thức?

2-x+y; $-5x^{2}y{z}^3+\frac{1}{3}x{y}^{2}z+x+1;\frac{x-y}{x{y}^2};\frac{1}{x}+2y-3z.$

Trả lời:

a)

• $\frac{1}{5}x{y}^2{z}^3$ là đơn thức;

• 3 - 2x3y2z không phải là đơn thức;

• $-\frac{3}{2}{x}^{4}yx{z}^2$ là đơn thức;

• $\frac{1}{2}{x}^2(y^3-z^3)$ không phải là đơn thức.

Vậy các biểu thức $\frac{1}{5}x{y}^2{z}^3;-\frac{3}{2}{x}^{4}yx{z}^2$ là đơn thức.

b)

• 2 – x + y là đa thức;

• $-5x^{2}y{z}^3+\frac{1}{3}x{y}^{2}z+x+1$ là đa thức;

• $\frac{x-y}{x{y}^2}$ không là đa thức;

• $\frac{1}{x}+2y-3z$ không là đa thức.

Vậy các biểu thức 2-x+y; $-5x^{2}y{z}^3+\frac{1}{3}x{y}^{2}z+x+1$ là đa thức.

Bài tập 2: Thu gọn mỗi đơn thức sau:

a) $-\frac{1}{2}{x}^{2}yx{y}^3$;

b) 0,5x2yzxy3.

Trả lời:

Thu gọn mỗi đơn thức sau: 

a. −12x2yxy3 = −12x2+1y3+1 = −12x3y4

b. 0,5x2yzxy3 = 0,5x2+1y3+1z = 0,5x3y4z 

Bài tập 3: Các đơn thức trong mỗi trường hợp sau có đồng dạng hay không? Vì sao?

a) $x^3{y}^5;-\frac{1}{6}{x}^3{y}^5$ và $\sqrt{3}{x}^3{y}^5$;

b) x2y3 và x2y7.

Trả lời:

Bài tập 4: Thực hiện phép tính:

a) 9x3y6 + 4x3y6 + 7x3y6;

b) 9x5y6 – 14x5y6 + 5x5y6.

Trả lời:

a) 9x3y6 + 4x3y6 + 7x3y6 = (9 + 4 + 7)x3y6 = 20x3y6;

b) 9x5y6 – 14x5y6 + 5x5y6 = (9 – 14 + 5)x5y6 = 0.

Bài tập 5: Thu gọn mỗi đa thức sau:

a) A = 13x2y + 4 + 8xy – 6x2y – 9;

b) B = 4,4x2y – 40,6xy2 + 3,6xy2 – 1,4x2y – 26.

Trả lời:

Thu gọn mỗi đa thức sau:

a. A = 13x2y+4+8xy−6x2y−9 = (13−6)x2y+8xy+(4−9) =  7x2y+8xy−5

b. B = 4,4x2y−40,6xy2+3,6xy2−1,4x2y−26 = (4,4−1,4)x2y−(40,6−3,6)xy2−26  = 3x2y−37xy2−26

Bài tập 6: Tính giá trị của đa thức P = x3y – 14y3 – 6xy2 + y + 2 tại x = –1; y = 2.

Trả lời:

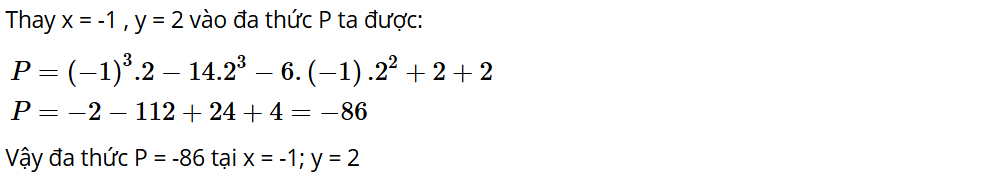
Bài tập 7:

a) Viết đa thức S biểu thị tổng diện tích các mặt của hình hộp chữ nhật có ba kích thước lần lượt là x (cm), 2y (cm), 3z (cm).

b) Tính giá trị của S tại x = 6; y = 2; z = 3.

Trả lời:

a) Hình hộp chữ nhật có ba kích thước lần lượt là x (cm), 2y (cm), 3z (cm). Khi đó:

Diện tích xung quanh của hình hộp chữ nhật đó là:

(x + 2y) . 3z = 3xz + 6yz (cm2).

Diện tích hai đáy của hình hộp chữ nhật đó là:

2 . x . 2y = 4xy (cm2).

Tổng diện tích các mặt của hình hộp chữ nhật là:

4xy + 3xz + 6yz (cm2).

Vậy đa thức S biểu thị tổng diện tích các mặt của hình hộp chữ nhật đã cho là:

S = 4xy + 3xz + 6yz (cm2).

b) Giá trị của S tại x = 6; y = 2; z = 3 là:

4 . 6 . 2 + 3 . 6 . 3 + 6 . 2 . 3 = 48 + 54 + 36 = 138.