Giải SGK Toán 8 Cánh Diều Bài 6: Hình thoi

Khởi động: Hoạ tiết trên vải ở Hình 55 gợi lên hình ảnh của hình thoi.

Hình thoi có những tính chất gì? Có những dấu hiệu nào để nhận biết một tứ giác là hình thoi?

Lời giải:

* Hình thoi có những tính chất:

- Các cạnh đối song song.

- Các góc đối bằng nhau.

- Hai đường chéo vuông góc với nhau và cắt nhau tại trung điểm của mỗi đường.

- Hai đường chéo là các đường phân giác của các góc ở đỉnh.

* Dấu hiệu nhận biết hình thoi:

- Hình bình hành có hai cạnh kề bằng nhau là hình thoi.

- Hình bình hành có hai đường chéo vuông góc với nhau là hình thoi.

I. Định nghĩa

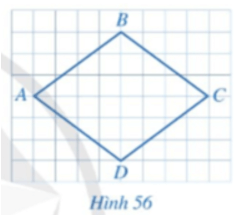
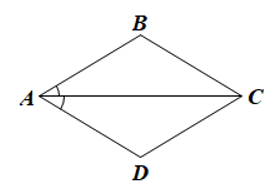
Hoạt động 1: So sánh độ dài các cạnh của tứ giác ABCD ở Hình 56.

Lời giải:

- Các cạnh của tứ giác ABCD ở hình 56 có độ dài bằng nhau.

II. Tính chất

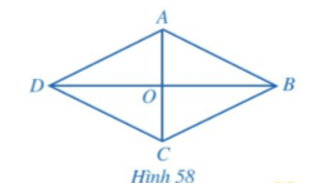
Hoạt động 2: Cho hình thoi ABCD có hai đường chéo AC và BD cắt nhau tại O (Hình 58).

a) Hình thoi ABCD có là hình bình hành hay không?

b) Hai đường chéo AC và BD có vuông góc với nhau hay không?

c) Hai tam giác ABC và ADC có bằng nhau hay không? Tia AC có phải là tia phân giác của ${\mathrm{BAD^\backslash widehat\{BAD\}BAD}}^{}$ hay không?

Lời giải:

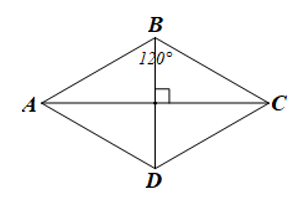
Luyện tập, vận dụng 1: Cho hình thoi ABCD có ${\mathrm{BAD^\backslash widehat\{BAD\}ABC}}^{}=120°$. Chứng minh tam giác ABD là tam giác đều.

Lời giải:

Do ABCD là hình thoi nên AB = AD

Tam giác ABD có AB = AD nên là tam giác cân tại A.

Do ABCD là hình thoi nên BD là tia phân giác của góc ABC.

Suy ra ${\mathrm{ABD^\backslash widehat\{ABD\}ABD}}^{}=\frac{1}{2}{\mathrm{ABD^\backslash widehat\{ABD\}ABC}}^{}=\frac{1}{2}.120°=60°$.

Xét ΔABD cân có $ABD^\backslash widehat\{ABD\}ABD=60°$ nên là tam giác đều.

III. Dấu hiệu nhận biết

Hoạt động 3: 

a) Cho hình bình hành ABCD có hai cạnh kề AB và BC bằng nhau. ABCD có phải là hình thoi hay không?

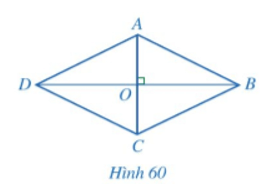
b) Cho hình bình hành ABCD có hai đường chéo AC và BD vuông góc với nhau (Hình 60).

• Đường thẳng AC có phải là đường trung trực của đoạn thẳng BD hay không?

• ABCD có phải là hình thoi hay không?

Lời giải:

a. ABCD là hình bình hành nên 2 cặp cạnh đối AB = DC và AD = BC. Mà theo giả thiết thì AB = BC => AB = DC = AD = BC. Vậy tứ giác ABCD có 4 cạnh bằng nhau nên là hình thoi. 

b. AC và BD là 2 đường chéo của hình bình hành nên giao điểm O là trung điểm của mỗi đường chéo => OD = OB. 

Kết hợp với AC vuông góc với BD tại O nên đường thẳng AC là đường trung trực của đoạn thẳng BD. 

Xét 2 tam giác vuông AOD và AOB có:

OA chung

OB = OD 

=> 2 tam giác vuông AOD và AOB bằng nhau theo trương hợp 2 cạnh góc vuông.

=> 2 cạnh tương ứng AD = AB (1)

Mặt khác ABCD là hình bình hành nên AD = BC, AB = DC. Kết hợp với (1)=> AD = BC =  AB = DC=> Tứ giác ABCD có 4 cạnh bằng nhau nên là hình thoi.

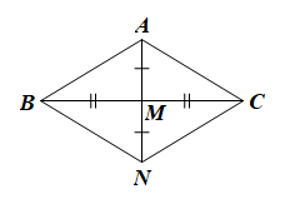
Luyện tập, vận dụng 2: Cho tam giác ABC cân tại A có M là trung điểm BC. Trên tia đối của tia MA lấy điểm N sao cho MN = MA. Chứng minh tứ giác ABNC là hình thoi.

Lời giải:

Tứ giác ABNC có: M là giao điểm của AN và BC

MN = MA

MB = MC (do M là trung điểm của BC)

Suy ra: tứ giác ABNC là hình bình hành (Tứ giác có 2 đường chéo cắt nhau tại trung điểm của mỗi đường)

Mà: AB = AC (do tam giác ABC cân tại A)

Suy ra: hình bình hành ABNC là hình thoi (Hình bình hành có 2 cạnh kề bằng nhau)

Bài tập

Bài tập 1: Cho hình bình hành ABCD có tia AC là tia phân giác của góc DAB. Chứng minh ABCD là hình thoi .

Lời giải:

Do AC là tia phân giác của góc DAB nên ${\mathrm{BAC^\backslash widehat\{BAC\}BAC}}^{}={\mathrm{DAC^\backslash widehat\{DAC\}DAC}}^{}$.

Mặt khác do ABCD là hình bình hành nên AB // CD

Suy ra ${\mathrm{BAC^\backslash widehat\{BAC\}BAC}}^{}={\mathrm{DCA^\backslash widehat\{DCA\}DCA}}^{}$ (so le trong).

Do đó ${\mathrm{DAC^\backslash widehat\{DAC\}DAC}}^{}={\mathrm{DCA^\backslash widehat\{DCA\}DCA}}^{}$ 

Xét ΔDAC có ${\mathrm{DAC^\backslash widehat\{DAC\}DAC}}^{}={\mathrm{DCA^\backslash widehat\{DCA\}DCA}}^{}$ nên ΔDAC cân tại D .

Suy ra DA = DC.

Hình bình hành ABCD có hai cạnh kề DA và DC bằng nhau nên là hình thoi.

Bài tập 2: Cho hình thoi ABCD có hai đường chéo AC và BD cắt nhau tại O. Chứng minh:

AC2 + BD2 = 4(OA2 + OB2) = 4AB2.

Lời giải:

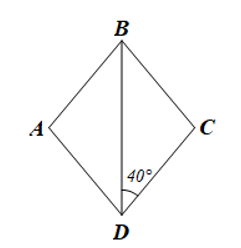
Bài tập 3: Cho hình thoi ABCD có $CDB^\backslash widehat\{CDB\}CDB=40°$. Tính số đo mỗi góc của hình thoi ABCD.

Lời giải:

Vì ABCD là hình thoi nên BD là phân giác của ${\mathrm{ADC^\backslash widehat\{ADC\}ADC}}^{}$ 

Do đó ${\mathrm{ADC^\backslash widehat\{ADC\}ADC}}^{}=2{\mathrm{CDB^\backslash widehat\{CDB\}CDB}}^{}=2.40°=80°$.

Suy ra ${\mathrm{ABC^\backslash widehat\{ABC\}ABC}}^{}={\mathrm{ADC^\backslash widehat\{ADC\}ADC}}^{}=80°$.

Do ABCD là hình thoi nên AB // CD, do đó ${\mathrm{BCD^\backslash widehat\{BCD\}BAD}}^{}+{\mathrm{ADC^\backslash widehat\{ADC\}ADC}}^{}=180°$

Suy ra $BCD^\backslash widehat\{BCD\}BAD=180°-{\mathrm{ADC^\backslash widehat\{ADC\}ADC}}^{}=180°-80°=100°$.

Do đó ${\mathrm{BCD^\backslash widehat\{BCD\}BCD}}^{}={\mathrm{BCD^\backslash widehat\{BCD\}BAD}}^{}=100°$.

Vậy ${\mathrm{ABC^\backslash widehat\{ABC\}ABC}}^{}={\mathrm{ADC^\backslash widehat\{ADC\}ADC}}^{}=80°$ và ${\mathrm{BCD^\backslash widehat\{BCD\}BCD}}^{}={\mathrm{BCD^\backslash widehat\{BCD\}BAD}}^{}=100°$.

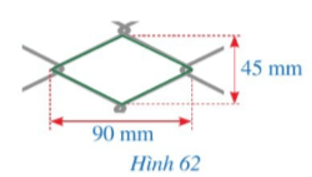
Bài tập 4: Hình 62 mô tả một lưới mắt cáo có dạng hình thoi với độ dài của hai đường chéo là 45 mm và 90 mm. Độ dài cạnh của ô lưới mắt cáo đó là bao nhiêu milimét (Làm tròn kết quả đến hàng đơn vị)?

Lời giải:

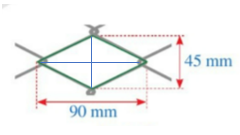
Độ dài cạnh của ô lưới mắt cáo đó là: 

(12.45)2+(12.90)2−−−−−−−−−−−−−−−√=50,3 (mm)

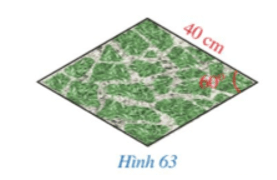
Bài tập 5: Một viên gạch trang trí có dạng hình thoi với độ dài cạnh là 40 cm và số đo một góc là 60° (Hình 63). Diện tích của viên gạch đó là bao nhiêu centimét vuông (làm tròn kết quả đến hàng phần trăm)?

Lời giải: