Giải SGK Toán 8 Cánh Diều Bài tập cuối chương I - Giải SGK Toán 8 - Cánh Diều

Bài tập 1: Cho hai đa thức: A = 4x6 – 2x2y3 – 5xy + 2; B = 3x2y3 + 5xy – 7.

a) Tính giá trị của mỗi đa thức A, B tại x = –1; y = 1.

b) Tính A + B; A – B.

Lời giải:

a. Tại x = -1, y = 1 thì:

A = 4x6−2x2y3−5xy+2

= 4(−1)6−2(−1)2.13−5(−1).1+2

= 4−2+5+2 = 9

B = 3x2y3+5xy−7.

= 3(−1)2.13+5(−1).1−7

= 3−5−7 =-5

A + B = (4x6−2x2y3−5xy+2)+(3x2y3+5xy−7)

= 4x6−2x2y3−5xy+2+3x2y3+5xy−7

= 4x6+x2y3−5

A - B = (4x6−2x2y3−5xy+2)-(3x2y3+5xy−7)

= 4x6−2x2y3−5xy+2−3x2y3−5xy+7

= 4x6−5x2y3−10xy+9

Bài tập 2: Thực hiện phép tính:

a) $- \frac{1}{3} a^{2} b (- 6 a b^{2} - 3 a + 9 b^{3})$ ;

b) (a2 + b2)(a4 – a2b2 + b4);

c) $(- 5 x y_{2}^{3} z) : (\frac{15}{2} x y^{2} z)$ ;

d) (8x4y2 – 10x2y4 + 12x3y5) : (– 2x2y2).

Lời giải:

a) $- \frac{1}{3} a^{2} b (- 6 a b^{2} - 3 a + 9 b^{3})$

$= (- \frac{1}{3} a^{2} b) . (- 6 a b^{2}) - (- \frac{1}{3} a^{2} b) . 3 a + (- \frac{1}{3} a^{2} b) . 9 b^{3}$

$= \frac{1}{3} a^{2} b . 6 a b^{2} + \frac{1}{3} a^{2} b . 3 a - \frac{1}{3} a^{2} b . 9 b^{3}$

= 2a3b3 + a3b – 3a2b4;

b) (a2 + b2)(a4 – a2b2 + b4);

= (a2 + b2)[(a2)2 – a2b2 + (b2)2]

= a3 + b3;

c) $(- 5 x y_{2}^{3} z) : (\frac{15}{2} x y^{2} z)$

$= ((- 5) : \frac{15}{2}) (x^{3} : x) (y^{2} : y^{2}) (z : z)$ ;

d) (8x4y2 – 10x2y4 + 12x3y5) : (– 2x2y2)

= 8x4y2 : (– 2x2y2) – 10x2y4 : (– 2x2y2) + 12x3y5 : (– 2x2y2)

= – 4x2 + 5y2 – 6xy3.

Bài tập 3: Viết mỗi hiệu sau dưới dạng bình phương, lập phương của một tổng hoặc một hiệu:

a) $x^{2} + \frac{1}{2} x + \frac{1}{16}$ ;

b) 25x2 – 10xy + y2;

c) x3 + 9x2y + 27xy2 + 27y3;

d) 8x3 – 12x2y + 6xy2 – y3.

Lời giải:

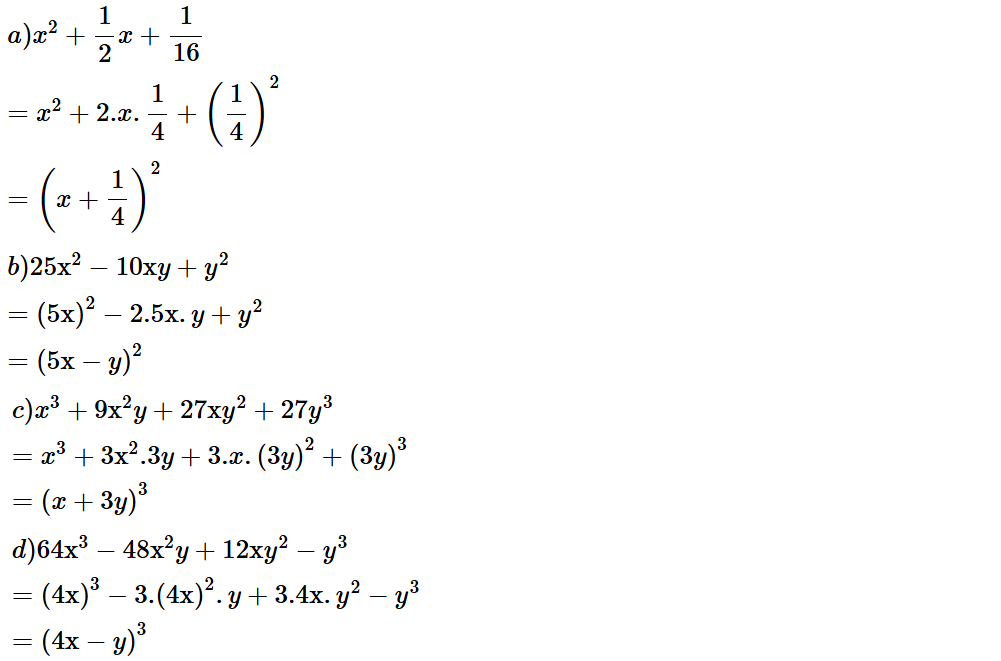
Bài tập 5: Chứng minh giá trị của mỗi biểu thức sau không phụ thuộc vào giá trị của biến:

a) A = 0,2(5x-1) - $\frac{1}{2} (\frac{2}{3} x + 4) + \frac{2}{3} (3 - x)$ ;

b) B = (x – 2y)(x2 + 2xy + 4y2) – (x3 – 8y3 + 10);

c) C = 4(x + 1)2 + (2x – 1)2 – 8(x – 1)(x + 1) – 4x.

Lời giải:

a) A = 0,2(5x-1) - $\frac{1}{2} (\frac{2}{3} x + 4) + \frac{2}{3} (3 - x)$

= x - 0,2 - $\frac{1}{3}$ x - 2 + 2 - $\frac{2}{3}$ x

= $= (x - \frac{1}{3} x - \frac{2}{3} x)$ + (2 - 0,2 - 2) = -0,2.

Vậy biểu thức A không phụ thuộc vào giá trị của biến.

b) B = (x – 2y)(x2 + 2xy + 4y2) – (x3 – 8y3 + 10)

= x3 – (2y)3 – x3 + 8y3 – 10 = – 8y3 + 8y3 – 10 = – 10.

Vậy biểu thức B không phụ thuộc vào giá trị của biến.

c) C = 4(x + 1)2 + (2x – 1)2 – 8(x – 1)(x + 1) – 4x.

= [2(x + 1)]2 + (2x – 1)2 – 8(x2 – 1) – 4x

= [2(x + 1)]2 + (2x – 1)2 – 8x2 + 8 – 4x

= [2(x + 1)]2 + (2x – 1)2 – 8x2 – 8x + 4x + 4 + 4

= [2(x + 1)]2 + (2x – 1)2 – 8x(x + 1) + 4(x + 1) + 4

= [2(x + 1)]2 + (2x – 1)2 + (x + 1)(4 – 8x) + 4

= [2(x + 1)]2 + (2x – 1)2 – 4(x + 1)(2x – 1) + 4

= [2(x + 1)]2 + (2x – 1)2 – 2 . 2(x + 1)(2x – 1) + 4

= [2(x + 1) – (2x – 1)]2 + 4

= (2x + 2 – 2x + 1)2 + 4

= 32 + 4 = 9 + 4 = 13.

Vậy biểu thức C không phụ thuộc vào giá trị của biến.

Bài tập 5: Phân tích mỗi đa thức sau thành nhân tử:

a) (x + 2y)2 – (x – y)2;

b) (x + 1)3 + (x – 1)3;

c) (2y – 3)x + 4y(2y – 3);

d) 10x(x – y) – 15x2(y – x);

e) x3 + 3x2 + 3x + 1 – y3;

g) x3 – 2x2y + xy2 – 4x.

Lời giải:

a) (x + 2y)2 – (x – y)2

= [(x + 2y) + (x – y)][(x + 2y) – (x – y)

= (x + 2y + x – y)(x + 2y – x + y)

= 3y(2x + y).

b) (x + 1)3 + (x – 1)3

= x3 + 3x2 + 3x + 1 + x3 – 3x2 + 3x – 1

= (x3 + x3) + (3x2 – 3x2) + (3x + 3x) + (1 – 1)

= 2x3 + 6x = 2x(x2 + 3);

c) (2y – 3)x + 4y(2y – 3) = (2y – 3)(x + 4y);

d) 10x(x – y) – 15x2(y – x) = 10x(x – y) + 15x2(x – y)

= (x – y)(10x + 15x2) = 5x(x – y)(2 + 3x) ;

e) x3 + 3x2 + 3x + 1 – y3 = (x + 1)3 – y3

= (x + 1 – y)[(x + 1)2 + (x + 1)y + y2]

= (x – y + 1)(x2 + 2x + 1 + xy + y + y2);

g) x3 – 2x2y + xy2 – 4x = x(x2 – 2xy + y2 – 4)

= x[(x – y)2 – 22] = x(x – y + 2)(x – y – 2).

Bài tập 6: Một mảnh vườn có dạng hình chữ nhật với chiều rộng là x (m), chiều dài là y (m).

a) Viết đa thức biểu thị diện tích của mảnh vườn.

b) Nếu tăng chiều rộng lên 2 m và giảm chiều dài đi 3 m thì được mảnh vườn mới. Viết đa thức biểu thị diện tích của mảnh vườn mới.

c) Viết đa thức biểu thị phần diện tích lớn hơn của mảnh vườn mới so với mảnh vườn ban đầu.

Lời giải:

a. Diện tích của mảnh vườn là: S=x.y

b. Diện tích của mảnh vườn mới là S1=(x+2)(y-3)

c. Phần diện tích lớn hơn của mảnh vườn mới so với mảnh vườn ban đầu:

S2 = S1 - S = (x+2)(y-3) - xy = xy - 3x + 2y - 6 - xy = - 3x + 2y - 6