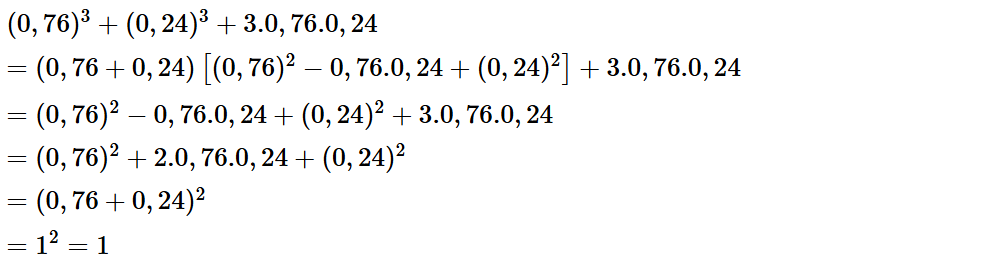Giải SGK Toán 8 Cánh Diều Bài 3: Hằng đẳng thức đáng nhớ

Khởi động: Diện tích của hình vuông MNPQ (Hình 4) có thể được tính theo những cách nào?

Lời giải:

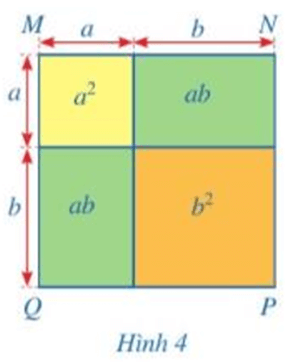
Ta đặt tên các điểm A, B, C, D như hình vẽ:

Diện tích của hình vuông MNPQ có thể được tính theo những cách sau:

- Cách 1. Tính theo tổng diện tích của 4 hình AMCE, ANDE, BEDP, BECQ.

- Cách 2. Tính theo tổng diện tích của 2 hình: MNDC, CDPQ.

- Cách 3. Tính theo tổng diện tích của 2 hình: ABQM, ABPN.

- Cách 4. Tìm độ dài một cạnh của hình vuông MNPQ rồi tính diện tích.

I. Hằng đẳng thức

Hoạt động 1: Xét hai biểu thức: P = 2(x + y) và Q = 2x + 2y. Tính giá trị của mỗi biểu thức P và Q rồi so sánh hai giá trị đó trong mỗi trường hợp sau:

a) Tại x = 1; y = −1;

b) Tại x = 2; y = −3.

Lời giải:

a. Tại x = 1; y = - 1

P = 2(1-1) = 0

Q = 2.1-2.1 = 0

=> P = Q

b. Tại x = 2; y = - 3

P = 2(2-3) = -2

Q = 2.2+2.(-3) = -2

=> P = Q

Luyện tập, vận dụng 1: Chứng minh rằng: x(xy2 + y) – y(x2y + x) = 0.

Lời giải:

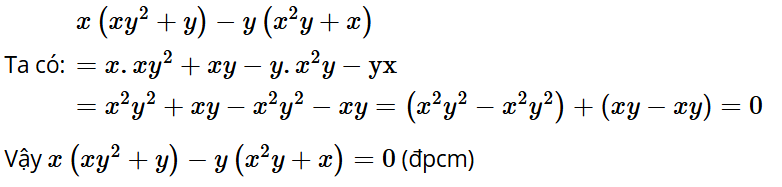
II. Hằng đẳng thức đáng nhớ

Hoạt động 2: Với a, b là hai số thực bất kì, thực hiện phép tính:

a) (a + b)(a + b);

b) (a – b)(a – b).

Lời giải:

a) (a + b)(a + b) = a . a + a . b + b . a + b . b = a2 + 2ab + b2;

b) (a – b)(a – b) = a . a – a . b – b . a + b . b = a2 – 2ab + b2.

Luyện tập, vận dụng 2: Tính:

a) ${\left(x+\frac{1}{2}\right)}^2$;

b) (2x + y)2;

c) (3 – x)2;

d) (x – 4y)2.

Lời giải:

a. (x+12)2 = x2+2.12x+(12)2 = x2+x+14

b. (2x+y)2 = (2x)2+2.2x.y+y2 = 4x2+4xy+y2 

c. (3−x)2 = 32−2.3.x+x2 = 32−6x+x2

d. (x−4y)2 = x2−2.x.4y+(4y)2 = x2−8xy+16y2

Luyện tập, vận dụng 3: Viết mỗi biểu thức sau dưới dạng bình phương của một tổng dạng bình phương của một tổng hoặc một hiệu:

a) $y^2+y+\frac{1}{4}$;

b) y2 + 49 – 14y.

Lời giải:

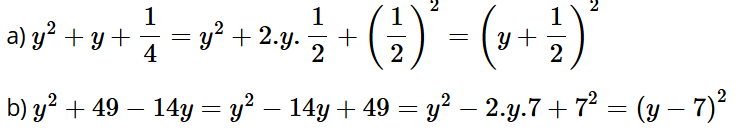
Luyện tập, vận dụng 4: Tính nhanh: 492.

Lời giải:

Ta có 492 = (50 – 1)2 = 502 – 2 . 50 . 1 + 12

= 2500 – 100 + 1 = 2400 + 1 = 2401.

Hoạt động 3: Với a, b là hai số thực bất kì, thực hiện phép tính: (a – b)(a + b).

Lời giải:

(a−b)(a+b)=a.a+a.b−b.a−b.b= a2−b2

Luyện tập, vận dụng 5: Viết mỗi biểu thức sau dưới dạng tích:

a) 9x2 – 16;

b) 25 – 16y2.

Lời giải:

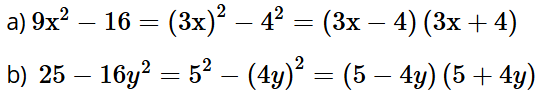
Luyện tập, vận dụng 6: Tính:

a) (a – 3b)(a + 3b);

b) (2x + 5)(2x – 5);

c) (4y – 1)(4y + 1).

Lời giải:

a) (a – 3b)(a + 3b) = a2 – (3b)2 = a2 – 9b2;

b) (2x + 5)(2x – 5) = (2x)2 – 52 = 4x2 – 25;

c) (4y – 1)(4y + 1) = (4y)2 – 1 = 16y2 – 1.

Luyện tập, vận dụng 7: Tính nhanh: 48 . 52.

Lời giải:

48 . 52 = (50-2)(50+2) = 502−22 = 2 500 - 4 = 2496

Hoạt động 4: Với a, b là hai số thực bất kì, thực hiện phép tính:

a) (a + b)(a + b)2;

b) (a – b)(a – b)2.

Lời giải:

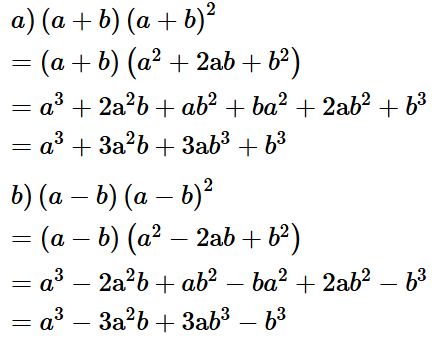
Luyện tập, vận dụng 8: Tính:

a) (3 + x)3;

b) (a + 2b)3;

c) (2x – y)3.

Lời giải:

a) (3 + x)3 = 33 + 3 . 32 . x + 3 . 3 . x2 + x3 = 27 + 27x + 9x2 + x3;

b) (a + 2b)3 = a3 + 3 . a2 . 2b + 3 . a . (2b)2 + (2b)3

= a3 + 6a2b + 12ab2 + 8b3;

c) (2x – y)3 = 2x3 – 3 . (2x)2 . y + 3 . 2x . y2 – y3

= 2x3 – 12x2y + 6xy2 – y3.

Luyện tập, vận dụng 9: Viết biểu thức sau dưới dạng lập phương của một hiệu: 8x3 – 36x2y + 54xy2 – 27y3.

Lời giải:

8x3−36x2y+54xy2−27y3 = (2x)3−3.(2x)2.3y+3.2x.(3y)2−(3y)3 = (2x−3y)3

Luyện tập, vận dụng 10: Tính nhanh: 1013 – 3 . 1012 + 3 . 101 – 1.

Lời giải:

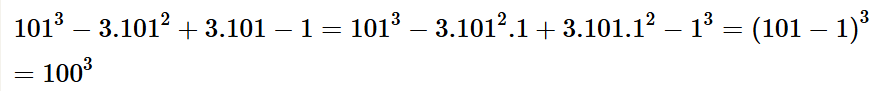
Hoạt động 5: Với a, b là hai số thực bất kì, thực hiện phép tính:

a) (a + b)(a2 – ab + b2);

b) (a – b)(a2 + ab + b2).

Lời giải:

a) (a + b)(a2 – ab + b2) = a . a2 – a . ab + a . b2 + b . a2 – b . ab + b . b2

= a3 – a2b + ab2 + a2b – ab2 + b3 = a3 + b3.

b) (a – b)(a2 + ab + b2) = a . a2 + a . ab + a . b2 – b . a2 – b . ab – b . b2

= a3 + a2b + a2b – a2b – a2b – b3 = a3 – b3.

Luyện tập, vận dụng 11: Viết mỗi biểu thức sau dưới dạng tích:

a) 27x3 + 1;

b) 64 – 8y3.

Lời giải:

Viết mỗi biểu thức sau dưới dạng tích:

a. 27x3+1 = (3x)3+13=(3x+1)((3x)2−3x.1+12)=(3x+1)(9x2−3x+1)

b. 64−8y3 = 43−8y3 = (4−8y)(42+4.8y+(8y)2) = (4−8y)(16+32y+64y2)

Bài tập

Bài tập 1: Viết mỗi biểu thức sau dưới dạng bình phương của một tổng hoặc một hiệu:

a) 4x2 + 28x + 49;

b) 4a2 + 20ab + 25b2;

c) 16y2 – 8y + 1;

d) 9x2 – 6xy + y2.

Lời giải:

a) 4x2 + 28x + 49 = (2x)2 + 2 . 2x . 7 + 72 = (2x + 7)2;

b) 4a2 + 20ab + 25b2 = (2a)2 + 2 . 2a . 5b + (5b)2 = (2a + 5b)2;

c) 16y2 – 8y + 1 = (4y)2 – 2 . 4y . 1 + 12 = (4y – 1)2;

d) 9x2 – 6xy + y2 = (3x)2 – 2 . 3x . y + y2 = (3x – y)2.

Bài tập 2: Viết mỗi biểu thức sau dưới dạng bình phương của một tổng hoặc một hiệu:

a) a3 +12a2 + 48a + 64;

b) 27x3 + 54x2y + 36xy2 + 8y3;

c) x3 – 9x2 + 27x – 27;

d) 8a3 – 12a2b + 6ab2 – b3.

Lời giải:

a. a3+12a2+48a+64

= a3+3.a2.4+3.a.42+43

= (a+4)3

b. 27x3+54x2y+36xy2+8y3

= (3x)3+3.(3x)2.2y+3.3x.(2y)2+(2y)3

= (3x+2y)3

c. x3−9x2y+27x−27

= x3−3.x2.3+3.x.32+33

= (x−3)3

d. 8a3−12a2b+6ab2−b3

= (2a)3−3.(2a)2b+3.2a.b2−b3

= (2a−b)3

Bài tập 3: Viết mỗi biểu thức sau dưới dạng tích:

a) 25x2 – 16;

b) 16a2 – 9b2;

c) 8x3 + 1;

d) 125x3 + 27y3;

e) 8x3 – 125;

g) 27x3 – y3.

Lời giải:

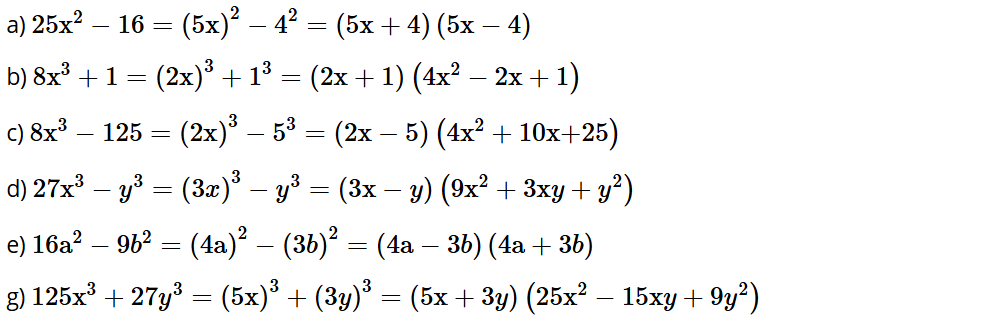
Bài tập 4: Tính giá trị của mỗi biểu thức:

a) A = x2 + 6x + 10 tại x = −103;

b) B = x3 + 6x2 + 12x + 12 tại x = 8.

Lời giải:

a) Ta có A = x2 + 6x + 10 = x2 + 6x + 9 + 1 = (x + 3)2 + 1.

Thay x = −103 vào biểu thức A, ta được:

A = (−103 + 3)2 + 1 = (−100)2 + 1 = 10 000 + 1 = 10 001.

Vậy A = 10 001 tại x = −103.

b) Ta có B = x3 + 6x2 + 12x + 12 = x3 + 3 . x2 . 2 + 3 . x . 22 + 23 + 4

= (x + 2)3 + 4.

Thay x = 8 vào biểu thức B, ta được:

B = (8 + 2)3 + 4 = 103 + 4 = 1004.

Vậy B = 1004 tại x = 8.

Bài tập 5: Chứng minh giá trị của mỗi biểu thức sau không phụ thuộc vào giá trị của biến x:

a) C = (3x – 1)2 + (3x + 1)2 – 2(3x – 1)(3x + 1);

b) D = (x + 2)3 – (x – 2)3 – 12(x2 + 1);

c) E = (x + 3)(x2 – 3x + 9) – (x – 2)(x2 + 2x + 4);

d) G = (2x – 1)(4x2 + 2x + 1) – 8(x + 2)(x2 – 2x + 4).

Lời giải:

a.

C= (3x−1)2+(3x+1)2−2(3x−1)(3x+1) 

= (3x−1)2+(3x+1)2−2(3x−1)(3x+1) 

=(3x−1)2−2(3x−1)(3x+1)+(3x+1)2 

= (3x−1−3x−1)2 

= (−2)2 

=4. 

Giá trị của biểu thức C luôn luôn bằng 4 với mọi x

b.

D = (x+2)3−(x−2)3−12(x2+1)

= (x+2)3−(x−2)3−12(x2+1)

= (x3+3.x2.2+3.x.22+23)−(x3−3.x2.2+3.x.22−23)−12x2−12

= x3+6x2+12.x+23−x3+6x2−12x+8−12x2−12=−4.

Giá trị của biểu thức D luôn luôn bằng -4 với mọi x

c.

E = (x+3)(x2−3x+9)−(x−2)(x2+2x+4)

= (x+3)(x2−3x+9)−(x−2)(x2+2x+4)

= (x.x2−x.3x+9x+3x2−9x+27)−(x.x2+x.2x+4x−2x2−2.2x−2.4)

= (x3−3x2+9x+3x2−9x+27)−(x3+2x2+4x−2x2−4x−8)

=(x3+27)−(x3−8)

= x3+27−x3+8

= 35

Giá trị của biểu thức E luôn luôn bằng 35 với mọi x

d.

G = (2x−1)(4x2+2x+1)−8(x+2)(x2−2x+4)

= (2x−1)(4x2+2x+1)−8(x+2)(x2−2x+4)

=(8x3+4x2+2x−4.x2−2x−1)−(8x3−16x2+32x+16x2−32x+64)

=(8x3−1)−(8x3+64)

=8x3−1−8x3−64

=−65.

Giá trị của biểu thức G luôn luôn bằng -65 với mọi x

Bài tập 6: Tính nhanh: (0,76)3 + (0,24)3 + 3.0,76.0,24.

Lời giải: