Giải SGK Toán 9 Chân trời sáng tạo Bài 1: Căn bậc hai

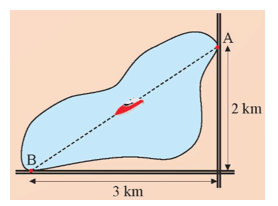
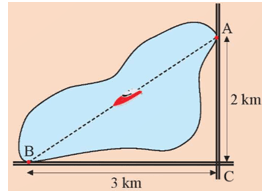
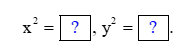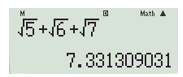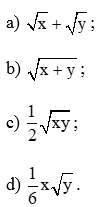Khởi động: Hai bến thuyền A và B nằm sát con đường vuông góc với nhau cách chỗ giao nhau lần lượt là 2 km và 3 km (hình bên). Một ca nô chạy thẳng từ A đến B. Quãng đường ca nô đi được dài bao nhiêu kilômét?

Trả lời:

Gọi C là giao điểm của hai con đường.

Xét tam giác ABC vuông tại C, áp dụng định lí Pythagore, ta có:

AB2 = AC2 + BC2 = 22 + 32 = 13.

Suy ra $AB=\sqrt{13}$ km .

Vậy quãng đường ca nô đi được dài $\sqrt{13}$  kilômét.

1. Căn bậc hai

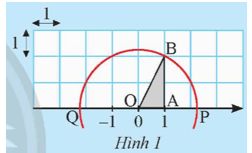
Khám phá 1: Cho trục số được vẽ trên lưới ô vuông đơn vị như Hình 1.

a) Tính độ dài cạnh huyền OB của tam giác vuông OAB.

b) Vẽ đường tròn tâm O bán kính OB, đường tròn này cắt trục số tại hai điểm P và Q.

Gọi x là số thực được biểu diễn bởi P, y là số thực được biểu diễn bởi Q.

Thay mỗi  bằng số thích hợp để có các đẳng thức:

Trả lời:

Thực hành 1: Tìm các căn bậc hai của mỗi số sau:

a) 36;

b) $\frac{4}{49}$ ;

c) 1,44;

d) 0.

Trả lời:

a) 36

b) 

c) 1,44

d) 0

Thực hành 2: Sử dụng dấu căn bậc hai để viết các căn bậc hai của mỗi số:

a) 11;

b) 2,5;

c) −0,09.

Trả lời:

a) Các căn bậc hai của 11 là $\sqrt{5}$ và - $\sqrt{5}$ .

b) Các căn bậc hai của 2,5 là $\sqrt{2,5}$  và -$\sqrt{2,5}$ .

c) Do −0,09 là số âm nên nó không tồn tại căn bậc hai.

Thực hành 3: Tính:

a) $\sqrt{1600}$ ;

b) $\sqrt{0,81}$ ;

c) $\sqrt{\frac{9}{25}}$ .

Trả lời:

a) $\sqrt{1600}$ = $\sqrt{{40}^2}=40$;

b) $\sqrt{0,81}$ $=\sqrt{0,9^2}=0,9$;

c) $\sqrt{\frac{9}{25}}$= ${\sqrt{{\left(\frac{3}{5}\right)}^2}}^{}=\frac{3}{5}$

Thực hành 4: Tính giá trị của các biểu thức:

a) ${\left(\sqrt{12}\right)}^2$;

b) ${\left(-\sqrt{0,36}\right)}^2$;

c) ${\left(\sqrt{5}\right)}^2+{\left(-\sqrt{1,21}\right)}^2$

Trả lời:

a) ${\left(\sqrt{12}\right)}^2$= 12

b) ${\left(-\sqrt{0,36}\right)}^2$= 0,36

c) ${\left(\sqrt{5}\right)}^2+{\left(-\sqrt{1,21}\right)}^2$ = 5+ 1,21 = 6,21

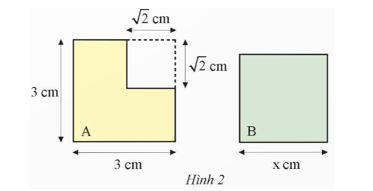
Vận dụng 1: Biết rằng hình A và hình vuông B trong Hình 2 có diện tích bằng nhau. Tính độ dài cạnh x của hình vuông B.

Trả lời:

Ta có diện tích hình A là:

3.3 - .  = 9 – 2 = 7

Mà diện tích hình A bằng diện tích hình vuông B:

=> x2 = 7

=> x =  

2.Tính căn bậc hai bằng máy tính cầm tay

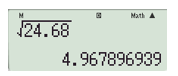
Thực hành 5: Sử dụng máy tính cầm tay, tính gần đúng các số sau (kết quả làm tròn đến chữ số thập phân thứ ba):

a) $\sqrt{11}$ ;

b) $\sqrt{7,64}$ ;

c) $\sqrt{\frac{2}{3}}$ .

Trả lời:

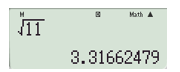
a) Để tính $\sqrt{11}$ , ấn liên tiếp các nút: 

Ta được kết quả như hình bên dưới:

Vậy $\sqrt{11}\approx 3,317$  (kết quả làm tròn đến chữ số thập phân thứ ba).

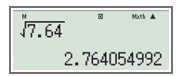
b) Để tính $\sqrt{7,64}$ ấn liên tiếp các nút:  

Ta được kết quả như hình bên dưới:

Vậy $\sqrt{7,64}\approx 2,764$ < (kết quả làm tròn đến chữ số thập phân thứ ba).

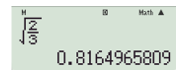
c) Để tính $\sqrt{\frac{2}{3}}$ , ấn liên tiếp các nút:        

Ta được kết quả như hình bên dưới:

Vậy $\sqrt{\frac{2}{3}}\approx 0,816$  (kết quả làm tròn đến chữ số thập phân thứ ba).

Thực hành 6: Sử dụng máy tính cầm tay để:

 a) Tìm các căn bậc hai của 10,08 (kết quả làm tròn đến chữ số thập phân thứ tư).

b) Tính giá trị của biểu thức $\frac{\sqrt{5}-1}{2}$ (kết quả làm tròn đến chữ số thập phân thứ năm).

Trả lời:

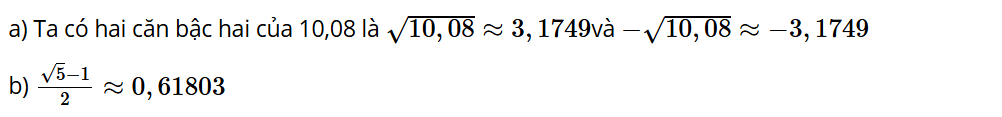
3. Căn thức bậc hai

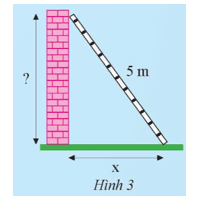
Khám phá 2: Một chiếc thang dài 5 m tựa vào bức tường như Hình 3.

a) Nếu chân thang cách chân tường x (m) thì đỉnh thang ở độ cao bao nhiêu so với chân tường?

b) Tính độ cao trên khi x nhận giá trị lần lượt là 1; 2; 3; 4.

Trả lời:

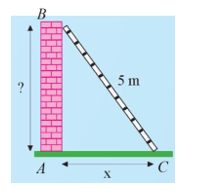
a) Gọi tam giác ABC như hình vẽ.

Trong thực tế bức tường vuông góc với mặt đất nên AB ⊥ AC.

Xét tam giác ABC vuông tại A, áp dụng định lí Pythagore, ta có:

BC2 = AB2 + AC2

 Suy ra AC2 = BC2 – AB2 = 52 – x2 = 25 – x2.

Do đó $AC=\sqrt{25-x^2}$(m) .

Vậy nếu chân thang cách chân tường x (m) thì đỉnh thang ở độ cao $\sqrt{25-x^2}$(m)  so với chân tường.

b) • Khi x = 1 thì độ cao đỉnh thang so với chân tường là: $\sqrt{25-1^2}=\sqrt{24}\left(m\right)$

• Khi x = 2 thì độ cao đỉnh thang so với chân tường là: $\sqrt{25-2^2}=\sqrt{25-4}=\sqrt{21}\left(m\right)$

• Khi x = 3 thì độ cao đỉnh thang so với chân tường là: $\sqrt{25-3^2}=\sqrt{25-9}=\sqrt{16}=4\left(m\right)$

• Khi x = 4 thì độ cao đỉnh thang so với chân tường là:$\sqrt{25-4^2}=\sqrt{25-16}=\sqrt{9}=3\left(m\right)$

Vậy x nhận giá trị lần lượt là 1; 2; 3; 4 thì độ cao đỉnh thang so với chân tường lần lượt là$\sqrt{24}m,\sqrt{21}m,4m,3m.$

Thực hành 7: Với giá trị nào của x thì biểu thức $A=\sqrt{3x+6}$ xác định? Tính giá trị của A khi x = 5 (kết quả làm tròn đến chữ số thập phân thứ hai)

Trả lời:

Để biểu thức A xác định thì 3x + 6  0

<=>3x  -6

<=>x  -2

Khi x = 5 ta có A =  =  = 4,58

Thực hành 8: Cho biểu thức $P=\sqrt{a^2-b^2}$Tính giá trị của P khi:

a) a = 5, b = 0;

b) a = 5, b = −5;

c) a = 2, b = −4.

Trả lời:

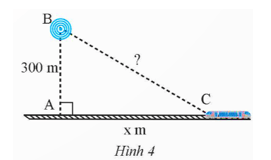
Vận dụng 2: Một trạm phát sóng được đặt ở vị trí B cách đường tàu một khoảng AB = 300 m. Đầu tàu đang ở vị trí C, cách vị trí A một khoảng AC = x (m) (Hình 4).

a) Viết biểu thức (theo x) biểu thị khoảng cách từ trạm phát sóng đến đầu tàu.

b) Tính khoảng cách trên khi x = 400, x = 1 000 (kết quả làm tròn đến hàng đơn vị của mét).

Trả lời:

a) Áp dụng định lí Pythagore vào tam giác vuông ABC, ta có:

BC2 = AB2 + AC2 = 3002 + x2.

Suy ra BC =  $\sqrt{{300}^2+x^2}$(m)

Vậy biểu thức (theo x) biểu thị khoảng cách từ trạm phát sóng đến đầu tàu là $\sqrt{{300}^2+x^2}$

b) Thay x = 400 thì khoảng cách từ trạm phát sóng đến đầu tàu là:

$\sqrt{{300}^2+{400}^2}=\sqrt{250000}=500$(m)

Thay x = 1 000 thì khoảng cách từ trạm phát sóng đến đầu tàu là:

$\sqrt{{300}^2+1{000}^2}=\sqrt{1090000}\approx 1044\left(m\right)$

Bài tập

Bài tập 1: Tìm các căn bậc hai của mỗi số sau:

a) 16;

b) 2 500;

c) $\frac{4}{81}$;

d) 0,09.

Trả lời:

a) 16;

b) 2 500;

c) 

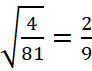
d) 0,09.

Bài tập 2: Tính:

a) $\sqrt{100}$ ;

b) $\sqrt{225}$ ;

c) $\sqrt{2,25}$ ;

d) $\sqrt{\frac{16}{225}}$ .

Trả lời:

a) $\sqrt{100}$= $\sqrt{{10}^2}=10$;

b) $\sqrt{225}$= $\sqrt{{15}^2}=15$;

c) $\sqrt{2,25}$= $\sqrt{{\left(1,5\right)}^2}$= 1,5;

d) $\sqrt{\frac{16}{225}}$= $\sqrt{{\left(\frac{4}{15}\right)}^2}=\frac{4}{15}$

Bài tập 3: Biết rằng 252 = 625, tìm các căn bậc hai của các số 625 và 0,0625.

Trả lời:

625 có hai căn bậc hai là 25 và – 25

0,0625 có hai căn bậc hai là 0,25 và – 0,25.

Bài tập 4: Sử dụng máy tính cầm tay, tính (kết quả làm tròn đến chữ số thập phân thứ tư):

a) $\sqrt{54}$ ;

b) $\sqrt{24,68}$ ;

c) $\sqrt{5}+\sqrt{6}+\sqrt{7}$.

Trả lời:

a) Để tính $\sqrt{54}$ , ấn liên tiếp các nút:      

Ta được kết quả như hình bên dưới:

Vậy $\sqrt{54}\approx 7,3485$  (kết quả làm tròn đến chữ số thập phân thứ tư).

b) Để tính $\sqrt{24,68}$ , ấn liên tiếp các nút:            

Ta được kết quả như hình bên dưới:

Vậy $\sqrt{24,68}\approx 4,9679$  (kết quả làm tròn đến chữ số thập phân thứ tư).

c) Để tính $\sqrt{5}+\sqrt{6}+\sqrt{7}$ , ấn liên tiếp các nút:

Ta được kết quả như hình bên dưới:

Vậy $\sqrt{5}+\sqrt{6}+\sqrt{7}\approx 7,3313$  (kết quả làm tròn đến chữ số thập phân thứ tư).

Bài tập 5: Tính giá trị của các biểu thức:

a) ${\left(\sqrt{5,25}\right)}^2+{(-\sqrt{1,75})}^2$ ;

b) ${\left(\sqrt{102}\right)}^2-\sqrt{{98}^2}$

Trả lời:

a) ${\left(\sqrt{5,25}\right)}^2+{(-\sqrt{1,75})}^2$ = 5, 25 + 1, 75 = 7

b) ${\left(\sqrt{102}\right)}^2-\sqrt{{98}^2}$= 102 - 98 = 4

Bài tập 6: Tìm x, biết:

a) x2 = 121;

b) 4x2 = 9;

c) x2 = 10.

Trả lời:

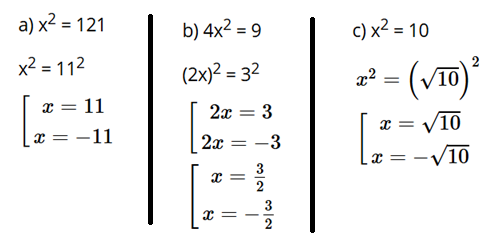
Bài tập 7: Tính giá trị của các biểu thức sau khi x = 16, y = 9:

Trả lời:

a) Thay x = 16, y = 9 vào biểu thức $\sqrt{x}+\sqrt{y}$ , ta có:

$\sqrt{16}+\sqrt{9}=\sqrt{4^2}+\sqrt{3^2}=4+3=7$

Vậy khi x = 16, y = 9 giá trị của các biểu thức bằng 7.

b) Thay x = 16, y = 9 vào biểu thức $\sqrt{x+y}$ , ta có:

$\sqrt{16+9}=\sqrt{25}=\sqrt{5^2}=5$

Vậy khi x = 16, y = 9 giá trị của các biểu thức bằng 5.

c) Thay x = 16, y = 9 vào biểu thức $\frac{1}{2}\sqrt{xy}$ , ta có:

$\frac{1}{2}\sqrt{16.9}=\frac{1}{2}\sqrt{144}=\frac{1}{2}\sqrt{{12}^2}=\frac{1}{2}.12=6$

Vậy khi x = 16, y = 9 giá trị của các biểu thức bằng 6.

d) Thay x = 16, y = 9 vào biểu thức $\frac{1}{6}x\sqrt{y}$ , ta có:

$\frac{1}{6}16\sqrt{9}=\frac{1}{6}.16.3=\frac{8}{3}.3=8$

Vậy khi x = 16, y = 9 giá trị của các biểu thức bằng 8.

Bài tập 8: Cho biểu thức $P=\sqrt{x^2-xy+1}$ Tính giá trị của P khi:

a) x = 3, y = −2;

b) x = 1, y = 4.

Trả lời:

a) x = 3, y = -2

P = 

b) x = 1, y = 4

P = 

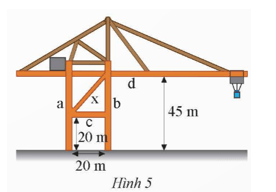
Bài tập 9: Trên cần trục ở Hình 5, hai trụ a và b đứng cách nhau 20 m, hai xà ngang c và d lần lượt có độ cao 20 m và 45 m so với mặt đất. Xà chéo x có độ dài bao nhiêu mét (kết quả làm tròn đến hàng đơn vị)?

Trả lời: