Giải SGK Toán 9 Chân trời sáng tạo Bài 2: Phương trình bậc nhất hai ẩn và hệ hai phương trình bậc nhất hai ẩn

Khởi động: Bài toán cổ:

Một đàn em nhỏ đứng bên sông

To nhỏ bàn nhau chuyện chia hồng

Mỗi người năm trái thừa năm trái

Mỗi người sáu trái một người không

Hỡi người bạn trẻ đang dừng bước

Có mấy em thơ, mấy trái hồng?

Làm thế nào để tính được số em nhỏ (em thơ) và số trái hồng?

Trả lời:

Gọi x là số em nhỏ, y là số quả hồng (x, y ∈ ℕ*).

– Câu “Mỗi người năm trái thừa năm trái” nên ta có 5x = y – 5.          (1)

– Câu “Mỗi người sáu trái một người không” nên ta có 6(x – 1) = y.    (2)

Để tính được số em nhỏ (em thơ) và số trái hồng thì ta tìm giá trị x, y thỏa mãn phương trình (1) và phương trình (2).

1. Phương trình bậc nhất hai ẩn

Khám phá 1: Để chuyển đổi từ độ F (kí hiệu x) sang độ C (kí hiệu y), ta dùng công thức: $y=\frac{5}{9}\left(x-32\right).$

a) Biến đổi công thức trên về dạng x – 1,8y = 32. (1)

b) Hỏi 20°C tương ứng với bao nhiêu độ F?

c) Hỏi 98,6°F tương ứng với bao nhiêu độ C?

Trả lời:

a) Ta có 

Nhân cả 2 vế với  ta có:

1,8y = x – 32

=> x – 1,8y = 32 (1)

b) Từ (1) ta có x = 32 + 1,8y

=> 20oC sẽ tương ứng với x = 32 + 1,8 . 20 = 68oF

c) Ta có 

=> 98,6oF sẽ tương ứng với y = = 37oC

Thực hành 1: Xác định các hệ số a, b, c của mỗi phương trình bậc nhất hai ẩn sau:

a) x + 5y = –4;

b) $\sqrt{3}x+y=0$;

c) $0x-\frac{3}{2}y=6$;

d) 2x + 0y = –1,5.

Trả lời:

a) x + 5y = –4 là phương trình bậc nhất hai ẩn với a = 1, b = 5, c = –4.

b) $\sqrt{3}x+y=0$ là phương trình bậc nhất hai ẩn với $a=\sqrt{3},b=\mathrm{1,}c=0$.

c) $0x-\frac{3}{2}y=6$ là phương trình bậc nhất hai ẩn với $a=\mathrm{0,}b=-\frac{3}{2},c=6$.

d) 2x + 0y = –1,5 là phương trình bậc nhất hai ẩn với a = 2, b = 0, c = –1,5.

Thực hành 2: Cho phương trình 3x + 2y = 4. (1)

a) Trong hai cặp số (1; 2) và (2; –1), cặp số nào là nghiệm của phương trình (1)?

b) Tìm y0 để cặp số (4; y0) là nghiệm của phương trình (1).

c) Tìm thêm hai nghiệm của phương trình (1).

d) Hãy biểu diễn tất cả các nghiệm của phương trình (1) trên mặt phẳng tọa độ Oxy.

Trả lời:

2. Hệ hai phương trình bậc nhất hai ẩn

Khám phá 2: Một ô tô từ A đến B, cùng lúc đó một xe máy đi từ B về A. Gọi x (km/h) là tốc độ của ô tô, y (km/h) là tốc độ của xe máy (x > 0, y > 0). Biết rằng:

(1) Tốc độ của ô tô hơn tốc độ xe máy 15 km/h;

(2) Quãng đường AB dài 210 km và hai xe gặp nhau sau 2 giờ.

a) Từ dữ kiện (1), hãy lập một phương trình hai ẩn x, y?

b) Từ dữ kiện (2), hãy lập thêm một phương trình hai ẩn x, y?

c) Bạn An khẳng định rằng tốc độ của ô tô và xe máy lần lượt là 60 km/h và 45 km/h. Có thể dùng hai phương trình lập được để kiểm tra khẳng định của bạn An là đúng hay sai không?

Trả lời:

a) Từ dữ kiện (1), ta có phương trình:

x = y + 15

b) Từ dữ kiện (2), ta có phương trình liên quan đến thời gian và quãng đường:

2x + 2y = 210

c) Bạn An khẳng định rằng tốc độ của ô tô và xe máy lần lượt là 60 km/h và 45 km/h. Để kiểm tra khẳng định này, ta thay vào phương trình (a) và phương trình (b):

Thay x = 60 và y = 45 vào phương trình (a):

60 = 45 + 15

60 = 60

Phương trình (a) đúng.

Thay x = 60 và y = 45 vào phương trình (b):

2.60 + 2.45 = 210

120 + 90 = 210

Phương trình (b) cũng đúng.

Vậy, dựa trên hai phương trình lập được và việc thay vào giá trị tốc độ của ô tô và xe máy, khẳng định của bạn An là đúng.

Thực hành 3: Trong các hệ phương trình sau, hệ phương trình nào là hệ hai phương trình bậc nhất hai ẩn?

a) $\{\begin{array}{c}x+3y=0\\ 4x-3y=-4;\end{array}$

b) $\{\begin{array}{c}\sqrt{3}x+0y=-5\\ 0x+\frac{4}{5}y=3;\end{array}$

c) $\{\begin{array}{c}7x+2y=-5\\ 0x+0y=9.\end{array}$

Trả lời:

Thực hành 4: Cho hệ phương trình $\{\begin{array}{c}x+5y=10\\ 2x-y=-13.\end{array}$. Trong hai cặp số (0; 2) và (–5; 3), cặp số nào là nghiệm của hệ phương trình đã cho?

Trả lời:

Cặp số (0; 2) không phải là nghiệm của hệ phương trình đã cho vì $\{\begin{array}{c}\left(-5\right)+5\cdot 3=10\\ 2\cdot \left(-5\right)-3=-13.\end{array}$

Cặp số (–5; 3) là nghiệm của hệ phương trình đã cho vì $\{\begin{array}{c}\left(-5\right)+5\cdot 5=10\\ 2\cdot \left(-5\right)-3=-13.\end{array}$

Vậy trong hai cặp số (0; 2) và (–5; 3), cặp số (–5; 3) là nghiệm của hệ phương trình đã cho.

Vận dụng: Đối với bài toán trong Hoạt động khởi động (trang 10), nếu gọi x là số em nhỏ, y là số quả hồng thì ta nhận được hệ hai phương trình bậc nhất hai ẩn nào?

Trả lời:

Ta có câu: “Mỗi người năm trái thừa năm trái”

=> 5x = y – 5

=> 5x – y = -5

Lại có “Mỗi người sáu trái một người không”

=> 6x = y + 6

=> 6x – y = 6

=> Ta có hệ hai phương trình bậc nhất hai ẩn

Bài tập

Bài tập 1: Trong các phương trình sau, phương trình nào là phương trình bậc nhất hai ẩn? Xác định các hệ số a, b, c của mỗi phương trình bậc nhất hai ẩn đó.

a) 2x + 5y = –7;

b) 0x – 0y = 5;

c) $0x-\frac{5}{4}y=3$;

d) 0,2x + 0y = –1,5.

Trả lời:

Bài tập 2: Trong các cặp số (1; 1), (–2; 5), (0; 2), cặp số nào là nghiệm của mỗi phương trình sau?

a) 4x + 3y = 7;

b) 3x – 4y = –1.

Trả lời:

a) Cặp số (1; 1) là nghiệm của phương trình 4x + 3y = 7 vì 4 . 1 + 3 . 1 = 4 + 3 = 7.

Cặp số (–2; 5) là nghiệm của phương trình 4x + 3y = 7 vì 4 . (–2) + 3 . 5 = –8 + 15 = 7.

Cặp số (0; 2) không phải là nghiệm của phương trình 4x + 3y = 7 vì 4 . 0 + 3 . 2 = 6 ≠ 7.

Vậy trong các cặp số đã cho thì có hai cặp số (1; 1) và (–2; 5) là nghiệm của phương trình 4x + 3y = 7.

a) Cặp số (1; 1) là nghiệm của phương trình 3x – 4y = –1 vì 3 . 1 – 4 . 1 = 3 – 4 = –1.

Cặp số (–2; 5) không phải là nghiệm của phương trình 3x – 4y = –1 vì 3 . (–2) – 4 . 5 = -6 – 20 = –26 ≠ –1.

Cặp số (0; 2) không phải là nghiệm của phương trình 3x – 4y = –1 vì 3 . 0 – 4 . 2 = 0 – 8 = –8 ≠ –1.

Vậy trong các cặp số đã cho thì có cặp số (1; 1) là nghiệm của phương trình 3x – 4y = –1.

Bài tập 3: Hãy biểu diễn tất cả các nghiệm của mỗi phương trình sau trên mặt phẳng tọa độ Oxy.

a) 2x + y = 3;

b) 0x – y = 3;

c) –3x + 0y = 2;

d) –2x + y = 0.

Trả lời:

a)

b)

c)

d)

Bài tập 4: Cho hệ phương trình $\{\begin{array}{c}4x-y=2\\ x+3y=7.\end{array}$. Cặp số nào dưới đây là nghiệm của hệ phương trình đã cho?

a) (2; 2);

b) (1; 2);

c) (–1; –2).

Trả lời:

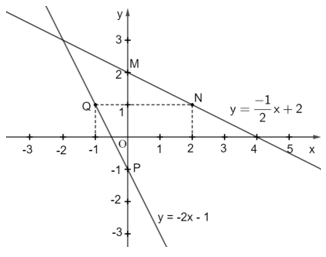
Bài tập 5: Cho hai đường thẳng $y=-\frac{1}{2}x+2$ và y = –2x – 1.

a) Vẽ hai đường thẳng đó trên cùng mặt phẳng tọa độ Oxy.

b) Xác định tọa độ giao điểm A của hai đường thẳng trên.

c) Tọa độ của điểm A có là nghiệm của hệ phương trình $\{\begin{array}{c}x+2y=4\\ 2x+y=-1\end{array}$ không? Tại sao?

Trả lời:

a) Đường thẳng $y=-\frac{1}{2}x+2$ đi qua điểm M(0; 2) và điểm N(2; 1).

Đường thẳng y = –2x – 1 đi qua điểm P(0; –1) và điểm Q(–1; 1).

Ta vẽ hai đường thẳng đó trên cùng mặt phẳng tọa độ Oxy như sau:

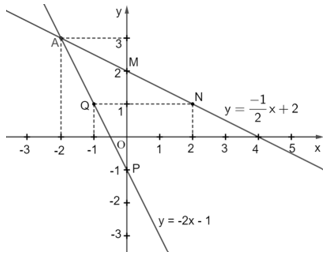
b) Giao điểm A của hai đường thẳng $y=-\frac{1}{2}x+2$ và y = –2x – 1 được biểu diễn như sau:

Dóng điểm A lên hai trục Ox và Oy, ta có A(–2; 3).

Vậy tọa độ giao điểm A của hai đường thẳng $y=-\frac{1}{2}x+2$ và y = –2x – 1 là A(–2; 3).

c) Cặp số (–2; 3) là nghiệm của hệ phương trình đã cho vì $\{\begin{array}{c}\left(-2\right)+2\cdot 3=4\\ 2\cdot \left(-2\right)+3=-1\end{array}$.

Do đó, tọa độ của điểm A có là nghiệm của hệ phương trình $\{\begin{array}{c}x+2y=4\\ 2x+y=-1\end{array}$.