Giải SGK Toán 9 Chân trời sáng tạo Bài tập cuối chương V

Câu hỏi trắc nghiệm

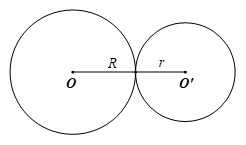
Bài tập 1: Cho hai đường tròn (O; 5 cm), (O’; 4 cm) với OO’ = 9 cm. Kết luận nào sau đây đúng về vị trí tương đối của hai đường tròn?

A. Hai đường tròn cắt nhau.

B. Hai đường tròn ở ngoài nhau.

C. Hai đường tròn tiếp xúc ngoài.

D. Hai đường tròn tiếp xúc trong.

Đáp án: C

Giải thích:

Ta có: 9 = 5 + 4 nên OO’ = R + r, suy ra hai đường tròn (O; 5 cm) và (O’; 4 cm) tiếp xúc ngoài.

Bài tập 2: Cho đường tròn (O; 6 cm) và đường thẳng a với khoảng cách từ O đến a là 4 cm. Kết luận nào sau đây đúng về vị trí giữa đường tròn (O) và đường thẳng a?

A. (O) và a cắt nhau tại hai điểm.

B. (O) và a tiếp xúc.

C. (O) và a không có điểm chung.

D. (O) và a có duy nhất điểm chung.

Đáp án: A

Giải thích:

Bài tập 3: Góc ở tâm là góc

A. có đỉnh nằm trên đường tròn

B. có đỉnh nằm trên bán kính của đường tròn.

C. có hai cạnh là hai đường kính của đường tròn.

D. có đỉnh trùng với tâm đường tròn.

Đáp án: C

Giải thích: Góc ở tâm là góc có đỉnh trùng với tâm đường tròn.

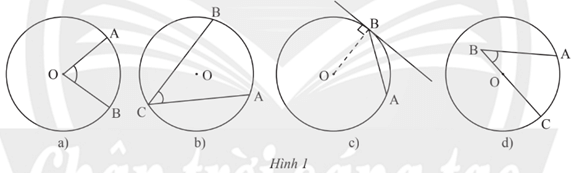
Bài tập 4: Hình nào dưới đây biểu diễn góc nội tiếp?

A. Hình 1a.

B. Hình 1b.

C. Hình 1c.

D. Hình 1d.

Đáp án: B

Giải thích: Góc nội tiếp là góc có đỉnh nằm trên đường tròn và hai cạnh chứa hai dây cung của đường tròn đó.

Bài tập 5: Góc nội tiếp chắn nửa đường tròn có số đo là

A. 180°.

B. 120°.

C. 90°.

D. 60°.

Đáp án: C

Giải thích: Góc nội tiếp chắn nửa đường tròn là góc vuông.

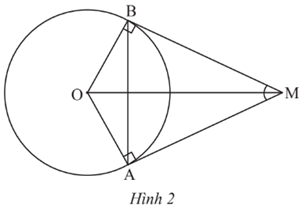
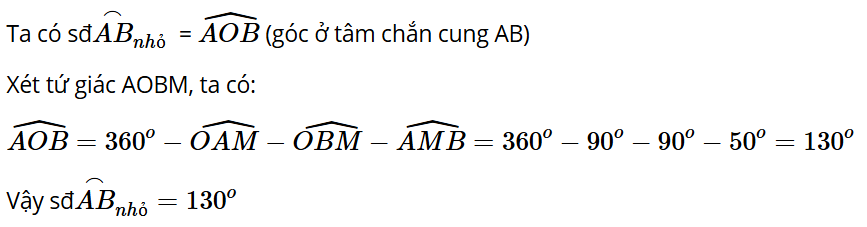
Bài tập 6: Cho hai tiếp tuyến của đường tròn (O) tại A và B cắt nhau tại M (Hình 2).

Biết ${\mathrm{AMB^\backslash widehat\{AMB\}AMB}}^{}=50°.$ Số đo cung nhỏ AB là

A. 140°.

B. 230°.

C. 130°.

D. 150°.

Đáp án: B

Giải thích: 

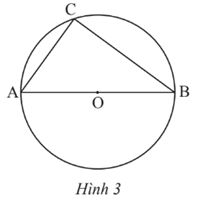
Bài tập 7: Trong Hình 3, $\widehat{\text{ACB}}$ là góc

A. vuông.

B. tù.

C. nhọn.

D. bẹt.

Đáp án: A

Giải thích:

Xét đường tròn (O) đường kính AB, có ${\text{ACB^widehat{ACB}ACB}}^{}$ là góc nội tiếp chắn nửa đường tròn nên ${\text{ACB^widehat{ACB}ACB}}^{}=90°.$

Bài tập 8: Trong một đường tròn, khẳng định nào sau đây là sai?

A. Các góc nội tiếp chắn nửa đường tròn là góc vuông.

B. Hai góc nội tiếp bằng nhau chắn hai cung bằng nhau.

C. Hai góc nội tiếp cùng chắn một cung thì bằng nhau.

D. Hai góc nội tiếp bằng nhau thì cùng chắn một cung.

Đáp án: D

Giải thích: Hai góc nội tiếp bằng nhau nhưng chưa chắc đã cùng chắn một cung.

Bài tập 9: Hình quạt tròn bán kính R, ứng với cung 90° có diện tích bằng

A. πR2.

B. $\frac{\pi {\text{R}}^2}{2}.$

C. $\frac{\pi {\text{R}}^2}{4}.$

D. $\frac{\pi {\text{R}}^2}{8}.$

Đáp án: C

Giải thích:

Diện tích hình quạt tròn bán kính R, ứng với cung 90° là:

$S=\frac{\pi R^{2}n}{360}=\frac{\pi R^2\cdot 90}{360}=\frac{\pi R^2}{4}.$

Bài tập 10: Hình vành khuyên giới hạn bởi hai đường tròn (O; 2 cm) và (O; 4 cm) có diện tích bằng

A. 12 cm2.

B. 24 cm2.

C. 4π cm2.

D. 12π cm2.

Đáp án: D

Giải thích:

Bài tập tự luận

Bài tập 11: Quan sát Hình 4. Biết ${\mathrm{DOA^\backslash widehat\{DOA\}DOA}}^{}=120°$, OA ⊥ OC, OB ⊥ OD.

a) Đọc tên các góc ở tâm có trong hình.

b) Tính số đo của mỗi góc ở tâm tìm được ở câu a.

c) Tìm các cặp cung bằng nhau và có số đo nhỏ hơn 180°.

d) So sánh hai cung nhỏ $\stackrel{}{AB}$ và $\stackrel{}{CD}.$

Trả lời:

Bài tập 12: Cho tam giác ABC có ba đỉnh nằm trên đường tròn (O) và AH là đường cao. Đường thẳng AO cắt đường tròn (O) tại điểm thứ hai D. Chứng minh rằng:

a) AC vuông góc với DC;

b) ${\mathrm{ABC^\backslash widehat\{ABC\}ABC}}^{}={\mathrm{ADC^\backslash widehat\{ADC\}ADC}}^{};$

c) AB.AC = AH.AD.

Trả lời:

a) Vì AD là đường kính của đường tròn (đường thẳng đi qua tâm và cắt đường tròn), nên góc ADC là góc nội tiếp chắn cung AC. Do đó, ADC là tam giác nội tiếp.

=> Tam giác ADC vuông tại C

=> AC vuông góc với DC

b) Ta có ADC là góc nội tiếp chắn cung AC

ABC là góc nội tiếp chắn cung AC

=> ABC = ADC

c) Xét tam giác ABH và tam giác ADC:

ABH = ADC

AHB = ACD = 90o

=> Tam giác ABH đồng dạng tam giác ADC

=> AB / AH = AD / AC

=> AB. AC = AD. AH

Bài tập 13: Hãy hoàn thành bảng số liệu sau vào vở (lấy π ≈ 3,14 và làm tròn kết quả đến hàng phần mười).

Trả lời:

Độ dài cung n°, bán kính R là: $l=\frac{\pi Rn}{180}\text{.}$

Suy ra $R=\frac{180l}{\pi n}$ và $n=\frac{180l}{\pi R}.$

Áp dụng các công thức trên, ta hoàn thành được bảng đã cho như sau:

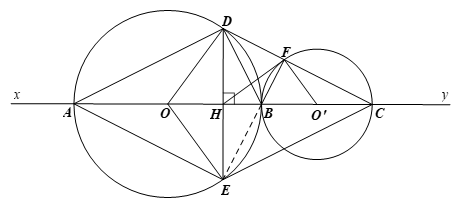
Bài tập 14: Trên đường thẳng xy, lấy lần lượt ba điểm A, B, C sao cho AB > BC. Vẽ đường tròn (O) đường kính AB và đường tròn (O’) đường kính BC.

a) Chứng minh rằng hai đường tròn (O) và (O’) tiếp xúc ngoài tại B.

b) Gọi H là trung điểm của AC. Vẽ dây DE của (O) vuông góc với AC tại H. Chứng minh tứ giác ADCE là hình thoi.

c) DC cắt đường tròn (O’) tại F. Chứng minh rằng ba điểm F, B, E thẳng hàng.

d) Chứng minh rằng HF là tiếp tuyến của đường tròn (O’).

Trả lời:

a) Ta có OO’ = OB + BO’ nên đường tròn (O) và (O’) tiếp xúc ngoài tại B.

b) Xét ∆ODE có OD = OE (cùng là bán kính của đường tròn (O) đường kính AB) nên ∆ODE cân tại O. Do đó đường cao OH đồng thời là đường trung tuyến của tam giác hay H là trung điểm của DE.

Xét tứ giác ADCE có hai đường chéo AC và DE cắt nhau tại trung điểm H của mỗi đường nên ADCE là hình bình hành.

Lại có DE ⊥ AC tại H nên hình bình hành ADCE là hình thoi.

c) Xét đường tròn (O) có AB là đường kính, $\widehat{ADB}$ là góc nội tiếp chắn nửa đường tròn nên ${\mathrm{ADB^\backslash widehat\{ADB\}ADB}}^{}=90°,$ do đó AD ⊥ DB.

Lại có AD // CE (do ADCE là hình thoi) nên DB ⊥ CE.

Xét ∆CDE có DB, CH là hai đường cao của tam giác cắt nhau tại B (do DB ⊥ CE và CH ⊥ DE) nên B là trực tâm của ∆CDE. Suy ra EF ⊥ CD. (1)

Xét đường tròn (O’) có BC là đường kính, $\widehat{BFC}$ là góc nội tiếp chắn nửa đường tròn nên ${\mathrm{BFC^\backslash widehat\{BFC\}BFC}}^{}=90°,$ do đó BF ⊥ CD. (2)

Từ (1) và (2) ta có EF, BF là hai đường thẳng cùng đi qua điểm F và vuông góc với CD nên là hai đường thẳng trùng nhau, hay ba điểm E, B, F thẳng hàng.

d) Vì BF ⊥ CD nên ${\mathrm{EFD^\backslash widehat\{EFD\}EFD}}^{}=90°,$ ∆DEF vuông tại F có FH là đường trung tuyến ứng với cạnh huyền nên $FH=\frac{1}{2}DE,$ mà H là trung điểm của DE nên $HE=\frac{1}{2}DE,$ do đó FH = HE.

Xét ∆HEF có FH = HE nên ∆HEF cân tại H. Do đó ${\mathrm{HFE^\backslash widehat\{HFE\}HFE}}^{}={\mathrm{HEF^\backslash widehat\{HEF\}HEF}}^{}$ (hai góc ở đáy bằng nhau).

Xét ∆O’BF có O’B = O’F (cùng là bán kính của đường tròn (O’) đường kính BC) nên ∆O’BF cân tại O’. Suy ra ${{\mathrm{O\prime FB^\backslash widehat\{O\text{'}FB\}O\prime FB}}^{}}^{}={{\mathrm{O\prime BF^\backslash widehat\{O\text{'}BF\}O\prime BF}}^{}}^{}$ (hai góc ở đáy bằng nhau).

Mà ${{\mathrm{O\prime BF^\backslash widehat\{O\text{'}BF\}O\prime BF}}^{}}^{}=\widehat{HBE}$ (đối đỉnh) nên ${{\mathrm{O\prime FB^\backslash widehat\{O\text{'}FB\}O\prime FB}}^{}}^{}={\mathrm{HBE^\backslash widehat\{HBE\}HBE}}^{}.$

Ta có: $\widehat{HFE}+{{\mathrm{O\prime FB^\backslash widehat\{O\text{'}FB\}O\prime FB}}^{}}^{}={\mathrm{HEF^\backslash widehat\{HEF\}HEF}}^{}+{\mathrm{HBE^\backslash widehat\{HBE\}HBE}}^{}=90°$ (do ∆HBE vuông tại H).

Hay ${\mathrm{HFO\prime ^\backslash widehat\{HFO\text{'}\}HFO\prime }}^{}=90°$ nên HF ⊥ O’F tại F.

Xét đường tròn (O’) có HF ⊥ O’F tại F thuộc đường tròn nên HF là tiếp tuyến của đường tròn (O’).

Bài tập 15: Hải đăng Kê Gà tọa lạc tại xã Tân Thành, huyện Hàm Thuận Nam, tỉnh Bình Thuận. Biết ngọn hải đăng cao 65 m so với mặt nước biển. Với khoảng cách bao nhiêu kilômét thì người quan sát trên tàu bắt đầu trông thấy ngọn của hải đăng này? Cho biết mắt người quan sát ở độ cao 5 m so với mặt nước biển và bán kính Trái Đất gần bằng 6 400 km.

Trả lời: