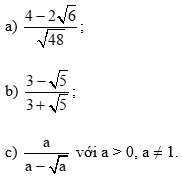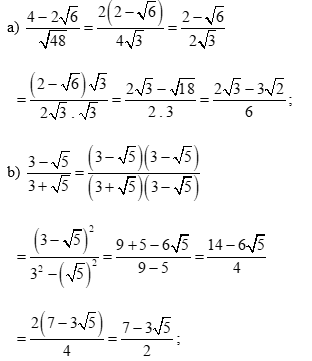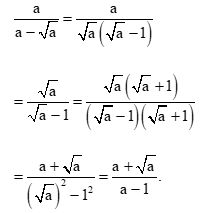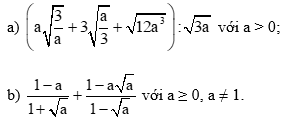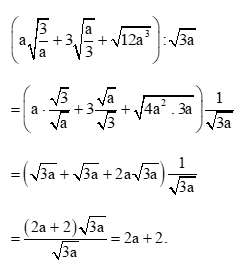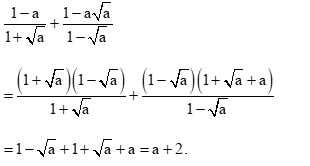Giải SGK Toán 9 Chân trời sáng tạo Bài tập cuối chương III

Câu hỏi trắc nghiệm

Bài tập 1: Biểu thức nào sau đây có giá trị khác với các biểu thức còn lại?

A. ${\left(-\sqrt{5}\right)}^2$.

B. $\sqrt{5^2}$.

C. $\sqrt{{\left(-\sqrt{5}\right)}^2}$.

D. $-{\left(\sqrt{5}\right)}^2$

Đáp án: D

Giải thích:

Ta có ${\left(-\sqrt{5}\right)}^2=\sqrt{5^2}=\sqrt{{\left(-5\right)}^2}=5;-{\left(\sqrt{5}\right)}^2=-5.$

Vậy biểu thức $-{\left(\sqrt{5}\right)}^2$  có giá trị khác với các biểu thức còn lại.

Bài tập 2: Có bao nhiêu số tự nhiên x để $\sqrt{16-x}$  là số nguyên?

A. 2.

B. 3.

C. 4.

D. 5.

Đáp án: D

Giải thích:

Bài tập 3: Giá trị của biểu thức $\sqrt{16}+\sqrt[3]{3-64}$ bằng

A. 0.

B. –2.

C. 8.

D. –4.

Đáp án: A

Giải thích:

Ta có $\sqrt{16}+\sqrt[3]{3-64}=\sqrt{4^2}+\sqrt[3]{3{\left(-4\right)}^3}=4+\left(-4\right)=0.$

Bài tập 4: Đẳng thức nào sau đây không đúng?

A. $\sqrt{16}+\sqrt{144}=16.$

B. $\sqrt{0,64}.\sqrt{9}=2,4.$

C. $\sqrt{{\left(-18\right)}^2}:\sqrt{6^2}=3.$

D. $\sqrt{{\left(-3\right)}^2}-\sqrt{7^2}=-10.$

Đáp án: D

Giải thích:

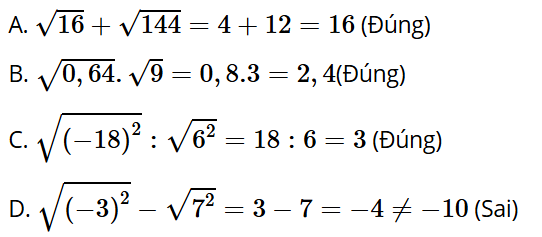
Bài tập 5: Biết rằng (2,6)2 = 6,76, giá trị của biểu thức $\sqrt{0,0676}$bằng

A. 0,0026.

B. 0,026.

C. 0,26.

D. 2,6.

Đáp án: C

Giải thích:

Ta có (2,6)2 = 6,76 suy ra $\sqrt{6,76}=\sqrt{{\left(2,6\right)}^2}=2,6.$

Do đó,$\sqrt{0,0676}=\sqrt{0,01.6,76}=\sqrt{0,01}.\sqrt{6,76}$ = 0,1 . 2,6 = 0,26.

Vậy $\sqrt{0,0676}=0,26.$

Bài tập 6: Rút gọn biểu thức $\sqrt{9a}-\sqrt{16a}+\sqrt{64a}$ với a ≥ 0, ta có kết quả

A. $15\sqrt{a}$ .

B. 15a.

C. $7\sqrt{a}$.

D. 7a.

Đáp án: C

Giải thích:

Với a ≥ 0, ta có: $\sqrt{9a}-\sqrt{16a}+\sqrt{64a}=3\sqrt{a}-4\sqrt{a}+8\sqrt{a}=7\sqrt{a}.$

Bài tập 7: Cho $a=2\sqrt{3}+\sqrt{2},b=3\sqrt{2}-2\sqrt{3}$ Rút gọn biểu thức $\sqrt{3}a-\sqrt{2}b$ ta có kết quả

A. $3\sqrt{6}$

B. $-\sqrt{6}$

C. $6\sqrt{3}$

D. $12-\sqrt{6}$

Đáp án: A

Giải thích:

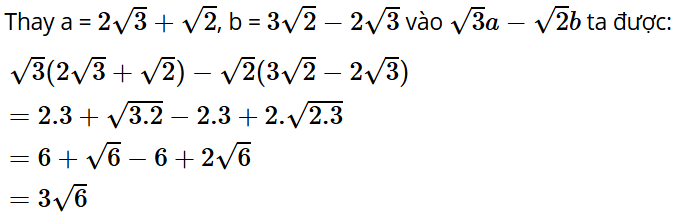
Bài tập 8: Trục căn thức ở mẫu biểu thức $\frac{\sqrt{6}-\sqrt{3}}{\sqrt{3}a}$với a > 0, ta có kết quả

A. $\frac{\sqrt{2}-1}{\sqrt{a}}$

B. $\frac{\left(\sqrt{6}-\sqrt{3}\right)\sqrt{a}}{3a}$

C. $\frac{\left(\sqrt{2}-1\right)\sqrt{a}}{a}$

D. $\sqrt{2a}-\sqrt{a}$

Đáp án: A

Giải thích:

Với a > 0, ta có: $\frac{\sqrt{6}-\sqrt{3}}{\sqrt{3a}}=\frac{\sqrt{3}\left(\sqrt{2}-1\right)}{\sqrt{3a}}=\frac{\sqrt{2}-1}{\sqrt{a}}$

Bài tập 9: Kết quả của phép tính $\sqrt{27}:\sqrt{6}.2\sqrt{18}$ là

A. 12.

B. 18.

C. 72.

D. 144.

Đáp án: B

Giải thích:

Ta có $\sqrt{27}:\sqrt{6}.2\sqrt{18}=\frac{\sqrt{27}}{\sqrt{6}}\cdot 2\sqrt{18}$

$=\sqrt{\frac{27}{6}}\cdot 6\sqrt{2}=\sqrt{\frac{9}{2}}\cdot 6\sqrt{2}$

$=\frac{\sqrt{9}}{\sqrt{2}}\cdot 6\sqrt{2}=3.6=18$

Bài tập 10: Rút gọn biểu thức $\frac{1}{2\sqrt{a}+\sqrt{2}}-\frac{1}{2\sqrt{a}-\sqrt{2}}$ với  $a\ge 0,a\ne \frac{1}{2},$ta có kết quả

A. $\frac{\sqrt{2}}{1-2a}$

B. $\frac{\sqrt{2}}{2a-1}$

C. $\frac{\sqrt{a}}{2a-1}$

D. $\frac{\sqrt{2}}{1-a}$

Đáp án: D

Giải thích:

Với $a\ge 0,a\ne \frac{1}{2},$  ta có:

$\frac{1}{2\sqrt{a}+\sqrt{2}}-\frac{1}{2\sqrt{a}-\sqrt{2}}$

$=\frac{1}{\sqrt{2}\left(\sqrt{a}+1\right)}-\frac{1}{\sqrt{2}\left(\sqrt{a}-1\right)}$

$=\frac{\left(\sqrt{a}-1\right)-\left(\sqrt{a}+1\right)}{\sqrt{2}\left(\sqrt{a}+1\right)\left(\sqrt{a}-1\right)}=\frac{\sqrt{a}-1-\sqrt{a}-1}{\sqrt{2}\left(a-1\right)}$

$=\frac{-2}{\sqrt{2}\left(a-1\right)}=\frac{-\sqrt{2}}{a-1}=\frac{\sqrt{2}}{1-a}$

Bài tập tự luận

Bài tập 11: Tìm x, biết:

a) x2 = 10;

b) $\sqrt{x}=8$ ;

c) x3 = −0,027;

d) $\sqrt[3]{3x}=-\frac{2}{3}$ .

Trả lời:

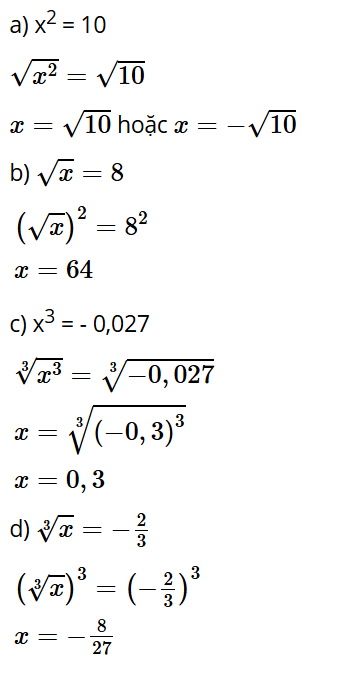
Bài tập 12: Biết rằng 1 < a < 5, rút gọn biểu thức $A=\sqrt{{\left(a-1\right)}^2}+\sqrt{{\left(a-5\right)}^2}$

Trả lời:

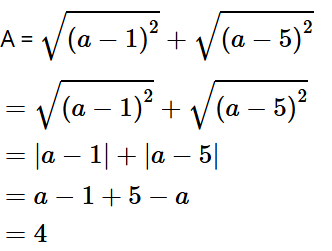
Bài tập 13: Trục căn thức ở mẫu các biểu thức sau:

Trả lời:

c) Với a > 0, a ≠ 1, ta có:

Bài tập 14: Biết rằng a > 0, b > 0 và ab = 16. Tính giá trị của biểu thức $A=a\sqrt{\frac{12b}{a}}+b\sqrt{\frac{3a}{b}}$

Trả lời:

A = 

A = 

A = 

A = 12

Bài tập 15: Tính $\frac{\sqrt{3}+\sqrt{2}}{\sqrt{3}-\sqrt{2}}-\frac{\sqrt{3}-\sqrt{2}}{\sqrt{3}+\sqrt{2}}.$

Trả lời:

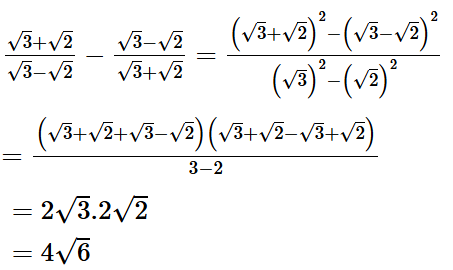
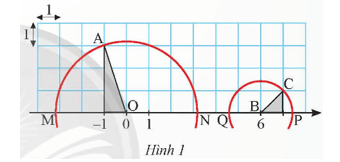
Bài tập 16: Một trục số được vẽ trên lưới ô vuông như Hình 1.

a) Đường tròn tâm O bán kính OA cắt trục số tại hai điểm M và N. Hai điểm M và N biểu diễn hai số thực nào?

a) Đường tròn tâm B bán kính BC cắt trục số tại hai điểm P và Q. Hai điểm P và Q biểu diễn hai số thực nào?

Trả lời:

a) Ta có $OA=\sqrt{3^2+1^2}=\sqrt{10}$  (áp dụng định lí Pythagore vào tam giác vuông).

Đường tròn tâm O bán kính OA cắt trục số tại hai điểm M và N nên OA, OM, ON đều là bán kính của đường tròn tâm O hay $OM=ON=OA=\sqrt{10}$.

Trong Hình 1, điểm M nằm bên trái gốc tọa độ, điểm N nằm bên phải gốc tọa độ.

Do đó, điểm M biểu diễn số thực $-\sqrt{10}$  và điểm N biểu diễn số thực $\sqrt{10}$ .

Vậy hai điểm M và N biểu diễn hai số thực lần lượt là $-\sqrt{10}$   và $\sqrt{10}$ .

b) Ta có $BC=\sqrt{1^2+1^2}=\sqrt{2}$  (áp dụng định lí Pythagore vào tam giác vuông).

Đường tròn tâm B bán kính BC cắt trục số tại hai điểm P và Q nên BC, BP, BQ đều là bán kính của đường tròn tâm B hay $BC=BP=BQ=\sqrt{2}$ .

Trong Hình 1:

• Điểm B biểu diễn số 6.

• Điểm P nằm bên phải điểm B nên điểm P biểu diễn số thực $6-\sqrt{2}$

• Điểm Q nằm bên trái điểm B nên điểm Q biểu diễn số thực $6+\sqrt{2}$ .

Vậy hai điểm P và Q biểu diễn hai số thực lần lượt là $6-\sqrt{2}$và $6+\sqrt{2}$

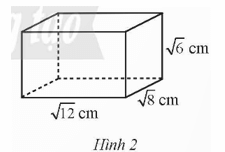
Bài tập 17: Cho hình hộp chữ nhật có chiều dài  $\sqrt{12}$ cm chiều rộng $\sqrt{8}$cm chiều cao $\sqrt{6}cm$như Hình 2

a) Tính thể tích của hình hộp chữ nhật đó.

a) Tính diện tích xung quanh của hình hộp chữ nhật đó.

Trả lời:

a) Thể tích của hình hộp chữ nhật là: 

b) Diện tích xung quanh của hình hộp chữ nhật là:  (cm)

Bài tập 18: Rút gọn các biểu thức sau:

Trả lời:

a) Với a > 0, ta có:

b) Với a ≥ 0, a ≠ 1, ta có:

Bài tập 19: Cho biểu thức  $P=\left(\frac{1}{a+\sqrt{a}}-\frac{1}{\sqrt{a}+1}\right):\frac{\sqrt{a}-1}{a+2\sqrt{a}+1}$với a > 0, a ≠ 1.

a) Rút gọn biểu thức P.

b) Tính giá trị của P khi a = 0,25.

Trả lời: