Khởi động: Hãy chỉ ra các bộ phận có dạng đường tròn của chiếc xe đạp trong hình dưới đây. Em hãy tìm thêm một số hình ảnh về đường tròn trong thực tế.
Trả lời:
⦁ Các bộ phận có dạng đường tròn của chiếc xe đạp trong hình trên là: bánh xe đạp (lốp xe, vành xe), đĩa xe đạp, líp xe đạp.
⦁ Một số hình ảnh về đường tròn trong thực tế: các đường tròn đồng tâm trên tấm bia bắn cung; guồng nước (cọn nước), viền khung mặt đồng hồ hình tròn, …
1. Khái niệm đường tròn
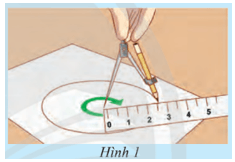
Khám phá 1: Mở một chiếc compa sao cho hai đầu compa cách nhau một khoảng R cho trước. Tì đầu nhọn của compa lên một điểm O cố định trên tờ giấy, xoay compa để đầu bút M của compa vạch trên giấy một đường cong. Nêu nhận xét về các khoảng cách từ một điểm M tuỳ ý trên đường cong vừa vẽ đến điểm O.
Trả lời:
- Khoảng cách từ một điểm M tuỳ ý trên đường cong vừa vẽ đến điểm O là không đổi và bằng R.
2. Tính đối xứng của đường tròn
Khám phá 2:
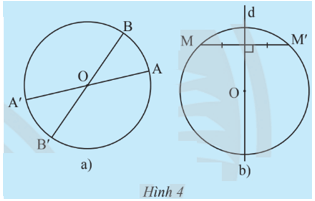
a) Cho đường tròn (O; R).
i) Lấy điểm A nằm trên đường tròn. Vẽ đường thẳng AO cắt đường tròn tại điểm A’ khác A. Giải thích tại sao O là trung điểm của đoạn thẳng AA’.
ii) Lấy điểm B khác A thuộc đường tròn (O; R). Tìm điểm B’ sao cho O là trung điểm của đoạn thẳng BB’. Điểm B’ có thuộc đường tròn (O; R) không? Giải thích.
b) Cho đường tròn (O; R), d là đường thẳng đi qua tâm O. Lấy điểm M nằm trên đường tròn. Vẽ điểm M’ sao cho d là đường trung trực của đoạn thẳng MM’ (khi M thuộc d thì lấy M’ trùng với M). Điểm M’ có thuộc đường tròn (O; R) không? Giải thích.
Trả lời:
a)
i) O là trung điểm của đoạn thẳng AA’ vì trong đường tròn (O;R): Hai điểm A và A’ đều cách điểm O một khoảng bằng R.
ii) Điểm B’ nằm đối xứng với B qua điểm O.
Điểm B’ cũng thuộc đường tròn (O;R) vì B nằm cách O một khoảng R nên B’ nằm cách O một khoảng R suy ra OB = OB’.
b) Điểm M’ cũng thuộc đường tròn (O;R) vì M’ là điểm đối xứng với M qua trung trực d.
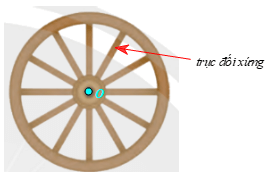
Thực hành 1: Xác định tâm đối xứng và trục đối xứng của bánh xe trong Hình 7. Giải thích cách làm.
Trả lời:
⦁ Tâm đối xứng O của bánh xe là trục của bánh xe (hình vẽ);
⦁ Trục đối xứng của bánh xe là là các nan vành của bánh xe (hình vẽ).
Vận dụng 1: Nêu cách chia một cái bánh có dạng hình tròn tâm O (Hình 8) thành hai phần bằng nhau.
Trả lời:
- Ta kẻ một đường thẳng đi qua tâm O của chiếc bánh ta sẽ được 2 phần bằng nhau
3. Đường kính và dây cung của đường tròn
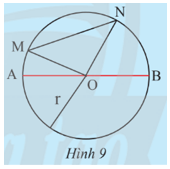
Khám phá 3: Trên đường tròn (O; R), lấy bốn điểm A, B, M, N sao cho AB đi qua O và MN không đi qua O (Hình 9).
a) Tính độ dài đoạn thẳng AB theo R.
b) So sánh độ dài của MN và OM + ON. Từ đó, so sánh độ dài của MN và AB.
Trả lời:
a) AB = AO + OB = R + R = 2R.
b) Ta có OM + ON = 2R > MN
Suy ra MN < AB.
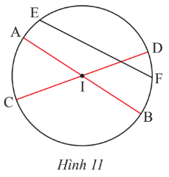
Thực hành 2: Cho đường tròn (I) có các dây cung AB, CD, EF. Cho biết AB và CD đi qua tâm I, EF không đi qua I (Hình 11). Hãy so sánh độ dài AB, CD, EF.
Trả lời:
Trong đường tròn (I), AB và CD là đường kính đi qua tâm I, EF là dây cung không đi qua I.
Do đó AB = CD và EF < AB, EF < CD.
Vậy EF < AB = CD.
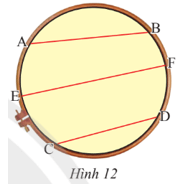
Vận dụng 2: Bạn Mai căng ba đoạn chỉ AB, CD, EF có độ dài lần lượt là 16 cm, 14 cm và 20 cm trên một khung thêu hình tròn bán kính 10 cm (Hình 12). Trong ba dây trên, dây nào đi qua tâm của đường tròn? Giải thích.
Trả lời:
Dây EF đi qua tâm của đường tròn vì EF = 20 = 2.10 = 2R
4. Vị trí tương đối của hai đường tròn
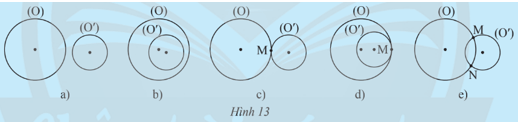
Khám phá 4: Tìm số điểm chung của hai đường tròn (O) và (O’) trong mỗi trường hợp sau:
Trả lời:
a) Không có điểm chung
b) Không có điểm chung
c) Một điểm chung M
d) Một điểm chung M
e) Hai điểm chung M và N.
Khám phá 5: Cho hai đường tròn phân biệt (O; R) và (O’; R’) với R ≥ R’. Hãy so sánh OO’ với R + R’ và R – R’ trong mỗi trường hợp sau:
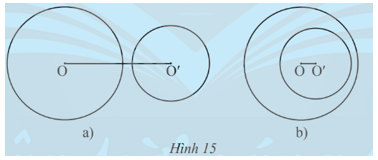
Trường hợp 1: (O; R) và (O’; R’) không có điểm chung (Hình 15).
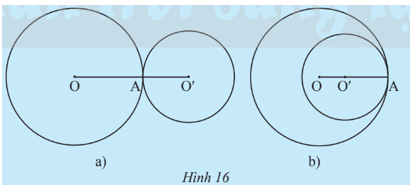
Trường hợp 2: (O; R) và (O’; R’) chỉ có một điểm chung (Hình 16).
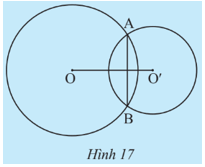
Trường hợp 3: (O; R) và (O’; R’) có đúng hai điểm chung (Hình 17).
Trả lời:
– Trường hợp 1: (O; R) và (O’; R’) không có điểm chung (Hình 15).
⦁ Hình 15a): OO’ > R + R’; OO’ > R – R’;
⦁ Hình 15b): OO’ < R + R’; OO’ < R – R’.
– Trường hợp 2: (O; R) và (O’; R’) chỉ có một điểm chung (Hình 16).
⦁ Hình 16a): OO’ = R + R’; OO’ > R – R’;
⦁ Hình 16b): OO’ < R + R’; OO’ = R – R’.
– Trường hợp 3: (O; R) và (O’; R’) có đúng hai điểm chung (Hình 17).
OO’ < R + R’; OO’ > R – R’.
Thực hành 3: Xác định vị trí tương đối giữa hai đường tròn (I; R) và (J; R’) trong mỗi trường hợp sau:
a) IJ = 5; R = 3; R’ = 2;
b) IJ = 4; R = 11; R’ = 7;
c) IJ = 6; R = 9; R’ = 4;
d) IJ = 10; R = 4; R’ = 1.
Trả lời:
a) IJ = 5; R = 3; R' = 2
Tổng bán kính: R + R' = 3 + 2 = 5
Hiệu bán kính: |R - R'| = |3 - 2| = 1
Khoảng cách giữa hai tâm (IJ = 5) bằng tổng bán kính (5 = 5), do đó hai đường tròn này tiếp xúc ngoài.
b) IJ = 4; R = 11; R' = 7
Tổng bán kính: R + R' = 11 + 7 = 18
Hiệu bán kính: |R - R'| = |11 - 7| = 4
Khoảng cách giữa hai tâm (IJ = 4) nhỏ hơn hiệu bán kính (4 < 18) và lớn hơn 0, nên hai đường tròn này cắt nhau.
c) IJ = 6; R = 9; R' = 4
Tổng bán kính: R + R' = 9 + 4 = 13
Hiệu bán kính: |R - R'| = |9 - 4| = 5
Khoảng cách giữa hai tâm (IJ = 6) nằm giữa hiệu bán kính và tổng bán kính (5 < 6 < 13), do đó hai đường tròn này cắt nhau.
d) IJ = 10; R = 4; R' = 1
Tổng bán kính: R + R' = 4 + 1 = 5
Hiệu bán kính: |R - R'| = |4 - 1| = 3
Khoảng cách giữa hai tâm (IJ = 10) lớn hơn tổng bán kính (10 > 5), nên hai đường tròn này không cắt nhau.
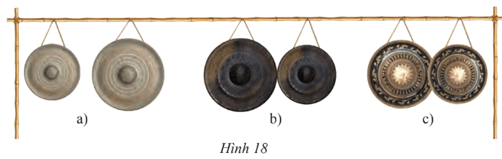
Vận dụng 3: Mô tả vị trí tương đối giữa mỗi cặp đường tròn trong hình chụp bộ cồng chiêng Tây Nguyên trong Hình 18.
Trả lời:
a) Hai đường tròn không giao nhau
b) Hai đường tròn tiếp xúc nhau
c) Hai đường tròn cắt nhau.
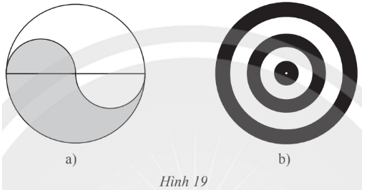
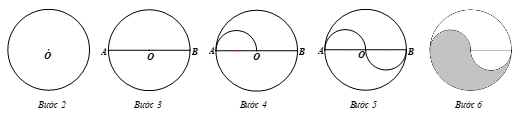
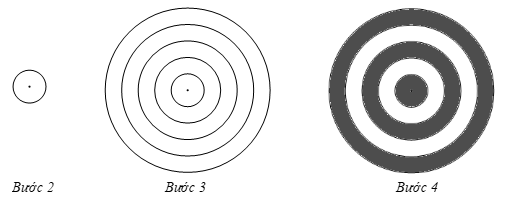
Vận dụng 4: Dùng compa đo bán kính và vẽ lại các hình trong Hình 19.
Trả lời:
– Hình 19a):
Bước 1. Đặt đầu nhọn vào tâm đường tròn lớn, mở cung của compa sao cho đầu bút nằm trên đường tròn lớn, ta đo được bán kính của đường tròn lớn.
Bước 2. Vẽ đường tròn với bán kính ta vừa đo được, ta được đường tròn lớn.
Bước 3. Kẻ đường kính AB của đường tròn lớn.
Bước 4. Vẽ nửa đường tròn đường kính OA sao cho nửa đường tròn nằm phía trên so với AB.
Bước 5. Vẽ nửa đường tròn đường kính OB sao cho nửa đường tròn nằm phía dưới so với AB.
Bước 6. Xóa tên các điểm vừa đặt, tô màu giống Hình 19a).
– Hình 19b):
Bước 1.
⦁ Đặt đầu nhọn vào tâm đường tròn nhỏ nhất, mở cung của compa sao cho đầu bút nằm trên đường tròn đó, ta đo được bán kính của đường tròn nhỏ nhất.
⦁ Vẽ đường tròn với bán kính ta vừa đo được, ta được đường tròn nhỏ nhất.
Bước 2.
⦁ Đặt đầu nhọn vào tâm đường tròn thứ hai, mở cung của compa sao cho đầu bút nằm trên đường tròn đó, ta đo được bán kính của đường tròn thứ hai.
⦁ Vẽ đường tròn có tâm trùng với tâm đường tròn nhỏ nhất, với bán kính ta vừa đo được, ta được đường tròn thứ hai.
Bước 3. Thực hiện lặp lại Bước 2 với 4 đường tròn còn lại.
Bước 4. Tô màu giống Hình 19b).
Bài tập
Bài tập 1: Cho đường tròn (O), bán kính 5 cm và bốn điểm A, B, C, D thoả mãn OA = 3 cm, OB = 4 cm, OC = 7 cm, OD = 5 cm. Hãy cho biết mỗi điểm A, B, C, D nằm trong, nằm trên hay nằm ngoài đường tròn (O).
Trả lời:
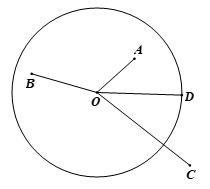
Điểm A: OA = 3 cm < 5 cm, nên điểm A nằm trong đường tròn (O).
Điểm B: OB = 4 cm < 5 cm, nên điểm B nằm trong đường tròn (O).
Điểm C: OC = 7 cm > 5 cm, nên điểm C nằm ngoài đường tròn (O).
Điểm D: OD = 5 cm, bằng bán kính của đường tròn, nên điểm D nằm trên đường tròn (O).
Bài tập 2: Cho hình chữ nhật ABCD có AD = 18 cm và CD = 12 cm. Chứng minh rằng bốn điểm A, B, C, D cùng thuộc một đường tròn. Tính bán kính của đường tròn đó.
Trả lời:

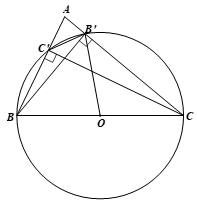
Bài tập 3: Cho tam giác ABC có hai đường cao BB’ và CC’. Gọi O là trung điểm của BC.
a) Chứng minh đường tròn tâm O bán kính OB’ đi qua B, C, C’.
b) So sánh độ dài hai đoạn thẳng BC và B’C’.
Trả lời:
a) Xét ∆BCB’ vuông tại B’ có đường trung tuyến B’O ứng với cạnh huyền BC, do đó
Mà O là trung điểm của BC nên
Do đó
Chứng minh tương tự đối với ∆BCC’ vuông tại C’, ta cũng có
Suy ra
Vậy đường tròn tâm O bán kính OB’ đi qua B, C, C’.
b) Xét đường tròn tâm O bán kính OB’, dây BC là đường kính đi qua tâm O, dây B’C’ là dây cung không đi qua tâm O.
Do đó BC > B’C’.
Bài tập 4: Cho tứ giác ABCD có
a) Chứng minh bốn điểm A, B, C, D cùng nằm trên một đường tròn.
b) So sánh độ dài của AC và BD.
Trả lời:

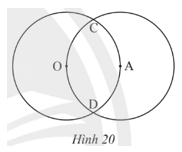
Bài tập 5: Cho hai đường tròn (O; 2 cm) và (A; 2 cm) cắt nhau tại C, D, điểm A nằm trên đường tròn tâm O (Hình 20).
a) Vẽ đường tròn (C; 2 cm).
b) Đường tròn (C; 2 cm) có đi qua hai điểm O và A không? Vì sao?
Trả lời:
a) Ta có hình vẽ
b) Đường tròn (C;2) có đi qua 2 điểm O và A. Vì OC = 2cm và CA = 2cm
Mà bán kính của đường tròn (C; 2cm) cũng là 2 cm nên đường tròn đi qua 2 điểm O và A
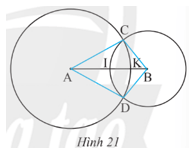
Bài tập 6: Cho hai đường tròn (A; 6 cm) và (B; 4 cm) cắt nhau tại C và D, AB = 8 cm. Gọi K, I lần lượt là giao điểm của hai đường tròn đã cho với đoạn thẳng AB (Hình 21).
a) Tính độ dài của các đoạn thẳng CA, CB, DA và DB.
b) Điểm I có phải là trung điểm của đoạn thẳng AB không?
c) Tính độ dài của đoạn thẳng IK.
Trả lời:
a) Vì hai đường tròn (A; 6 cm) và (B; 4 cm) cắt nhau tại C và D nên C, D cùng nằm trên hai đường tròn (A; 6 cm) và (B; 4 cm), do đó AC = AD = 6 cm và BC = BD = 4 cm.
b) Do I là giao điểm của đường tròn (B; 4 cm) với đoạn thẳng AB nên I nằm giữa hai điểm A, B và I nằm trên đường tròn (B; 4 cm), do đó BI = 4 cm.
Vì I nằm giữa hai điểm A, B nên ta có: AI + IB = AB
Suy ra AI = AB – IB = 8 – 4 = 4 (cm).
Ta có I nằm giữa hai điểm A, B và AI = BI nên I là trung điểm của đoạn thẳng AB.
c) Do K là giao điểm của đường tròn (A; 6 cm) với đoạn thẳng AB nên K nằm trên đường tròn (A; 6 cm), do đó AK = 6 cm.
Ta có AI < AK (4 cm < 6 cm) nên I nằm giữa hai điểm A, K.
Do đó AI + IK = AK
Suy ra IK = AK – AI = 6 – 4 = 2 (cm).
Vậy IK = 2 cm.
Bài tập 7: Xác định vị trí tương đối của (O; R) và (O’; R’) trong mỗi trường hợp sau:
a) OO’ = 18; R = 10; R’ = 6;
b) OO’ = 2; R = 9; R’ = 3;
c) OO’ = 13; R = 8; R’ = 5;
d) OO’ = 17; R = 15; R’ = 4.
Trả lời:
a) OO' = 18; R = 10; R' = 6;
Tổng bán kính: R + R' = 10 + 6 = 16
Hiệu bán kính: |R - R'| = |10 - 6| = 4
Trong trường hợp này, OO' lớn hơn tổng bán kính (18 > 16), nên hai đường tròn này không giao nhau.
b) OO' = 2; R = 9; R' = 3;
Tổng bán kính: R + R' = 9 + 3 = 12
Hiệu bán kính: |R - R'| = |9 - 3| = 6
Trong trường hợp này, OO' nhỏ hơn hiệu bán kính (2 < 6), nên hai đường tròn này giao nhau.
c) OO' = 13; R = 8; R' = 5;
Tổng bán kính: R + R' = 8 + 5 = 13
Hiệu bán kính: |R - R'| = |8 - 5| = 3
Trong trường hợp này, OO' bằng tổng bán kính (13 = 13), nên hai đường tròn này tiếp xúc ngoài.
d) OO' = 17; R = 15; R' = 4.
Tổng bán kính: R + R' = 15 + 4 = 19
Hiệu bán kính: |R - R'| = |15 - 4| = 11
Trong trường hợp này, OO' lớn hơn hiệu bán kính (17 > 11), nên hai đường tròn này không giao nhau.