Giải SGK Toán 11 Chân trời sáng tạo Bài 2: Giới hạn của hàm số

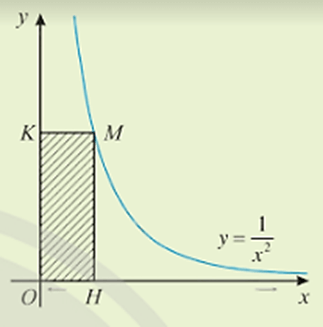
Hoạt động khởi động: Quan sát hình bên, cho biết hình chữ nhật OHMK thay đổi nhưng điểm M luôn nằm trên đồ thị hàm số $y=\frac{1}{x^2}$ (x > 0). Diện tích hình chữ nhật sẽ thay đổi như thế nào khi điểm H tiến gần đến gốc tọa độ? Khi H tiến xa sang phía bên phải thì sao?

Trả lời:

SOMHK=OH.OK=xH.yH=xH.1x2H=1xH

Khi H tiến đến gần gốc toạ độ, tức là xH càng nhỏ. Vậy điện tích OMHK càng lớn

Khi H tiến xa sang phía bên phải, tức là xH càng lớn. Vậy điện tích OMHK càng nhỏ

1. Giới hạn hữu hạn của hàm số tại một điểm

Khám phá 1: Xét hàm số $y=f\left(x\right)=\frac{2x^2-2}{x-1}$.

a) Bảng sau đây cho biết giá trị của hàm số tại một số điểm gần điểm 1.

Có nhận xét gì về giá trị của hàm số khi x càng gần đến 1?

b) Ở Hình 1, M là điểm trên đồ thị hàm số y = f(x); H và P lần lượt là hình chiếu của M trên trục hoành và trục tung. Khi điểm H thay đổi gần về điểm (1; 0) trên trục hoành thì điểm P thay đổi như thế nào?

Trả lời:

a) Khi x càng gần đến 1 thì giá trị của f(x) gần đến giá trị 4.

b) Khi điểm H thay đổi gần về điểm (1; 0) trên trục hoàng thì điểm P gần về điểm (0; 4).

Thực hành 1: Tìm các giới hạn sau:

a) limx→3(2x2−x)

b) limx→−1=x2+2x+1x+1

Trả lời:

a) limx→3(2x2−x)=2.32−3=15

b) limx→−1x2+2x+1x+1=limx→−1(x+1)2x+1=limx→−1(x+1)=−1+1=0

2. Các phép toán về giới hạn hữu hạn của hàm số

Khám phá 2: Cho hai hàm số y = f(x) = 2x và y = g(x) = $\frac{x}{x+1}$.

a) Giả sử (xn) là dãy số bất kì thỏa mãn xn ≠ – 1 với mọi n và xn → 1 khi n → +∞. Tìm giới hạn lim[f(xn) + g(xn)].

b) Từ đó, tìm giới hạn $\underset{x\to 1}{\lim }\text{[}f\left(x\right)+g\left(x\right)\text{]}$, và so sánh với $\underset{x\to 1}{\lim }f\left(x\right)+\underset{x\to 1}{\lim }g\left(x\right)$.

Trả lời:

+) Hàm số y = f(x) = 2x xác định trên $R$.

Dãy số (xn) bất kì thỏa mãn xn ≠ – 1 với mọi n và xn → 1 khi n → +∞, ta có:

limf(xn) = lim(2xn) = 2.limxn = 2.1 = 2.

Suy ra$\underset{x\to 1}{\lim }f\left(x\right)$ = 2.

+) Hàm số y = g(x) = $\frac{x}{x+1}$ xác định trên ℝ \ {2}.

Dãy số (xn) bất kì thỏa mãn xn ≠ – 1 với mọi n và xn → 1 khi n → +∞, ta có:

limg(xn) =$\lim \frac{x_n}{x_n+1}=\frac{1}{2}$.

Suy ra $\underset{x\to -1}{\lim }g\left(x\right)=\frac{1}{2}$.

a) Ta có: lim[f(xn) + g(xn)] = limf(xn) + limg(xn) = $2+\frac{1}{2}=\frac{5}{2}$.

b) Ta có $\text{lim[}f\left(x_n\right)+g\left(x_n\right)\text{]=}\frac{5}{2}$ nên $\underset{x\to 1}{\lim }\text{[}f\left(x\right)+g\left(x\right)\text{]=}\frac{5}{2}$.

Ta lại có: $\underset{x\to 1}{\lim }f\left(x\right)+\underset{x\to 1}{\lim }g\left(x\right)=2+\frac{1}{2}=\frac{5}{2}$.

Vì vậy $\underset{x\to 1}{\lim }\text{[}f\left(x\right)+g\left(x\right)\text{]=}\underset{x\to 1}{\lim }f\left(x\right)+\underset{x\to 1}{\lim }g\left(x\right)$.

Thực hành 2: Tìm các giới hạn sau:

a) limx→−2(x2+5x−2)

b) limx→1x2−1x−1

Trả lời:

a) limx→−2(x2+5x−2)=limx→−2x2+limx→−2(5x)−limx→−22

=(−2)2+5limx→−2x−2=4+5.(−2)−2=−8

b) limx→1x2−1x−1=limx→1(x+1)(x−1)x−1=limx→1(x+1)=limx→1x+limx→11=1+1=2

3. Giới hạn một phía

Khám phá 3: Giá cước vận chuyển bưu kiện giữa hai thành phố do một đơn vị cung cấp được cho bởi bảng sau: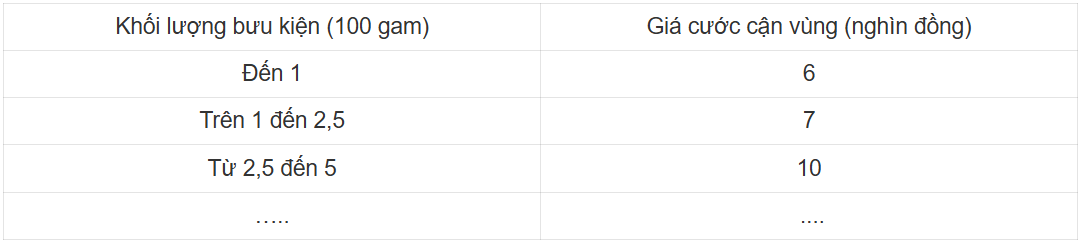

Nếu chỉ xét trên khoảng từ 0 đến 5 (tính theo 100 gam) thì hàm số giá cước (tính theo nghìn đồng) xác định như sau:

f(x)=⎧⎩⎨⎪⎪6;x∈(0;1]7;x∈(1;2,5]10;x∈(2,5;5]

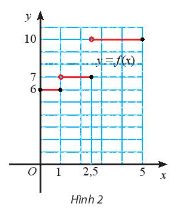
Đồ thị hàm số như Hình 2

a) Giả sử (xn) là dãy số bất kì sao cho xn∈(1;2,5) và limxn=1. Tìm limf(xn)

b) Giả sử (x′n) là dãy số bất kì sao cho x′n∈(0;1) và limx′n=1. Tìm limf(x′n)

c) Nhận xét về kết quả ở a) và b)

Trả lời:

Thực hành 3: Cho hàm số f(x)={1−2x;x≤−1x2+2;x>−1.

Tìm các giới hạn limx→−1+f(x),limx→−1−f(x) và limx→−1f(x) (nếu có)

Trả lời:

+) Với dãy số (xn) bất kì, xn ≤ – 1 và xn → – 1. Khi đó f(xn) = 1 – 2xn nên limf(xn) = lim(1 – 2xn) = 3.

Vì vậy $\underset{x\to -1^{-}}{\lim }f\left(x\right)=3$.

+) Với dãy số (xn) bất kì, xn > – 1 và xn → – 1. Khi đó f(xn) = $x_n^2+2$ nên limf(xn) = lim($x_n^2+2$) = 3.

Vì vậy $\underset{x\to -1^{+}}{\lim }f\left(x\right)=3$.

Vì $\underset{x\to -1^{+}}{\lim }f\left(x\right)=\underset{x\to -1^{-}}{\lim }f\left(x\right)=3$ nên $\underset{x\to -1}{\lim }f\left(x\right)=3$.

4. Giới hạn hữu hạn của hàm số tại vô cực

Khám phá 4: Cho hàm số f(x)=1x có đồ thị như Hình 3.

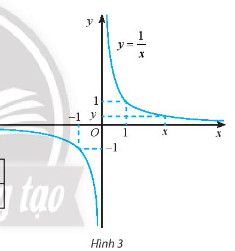
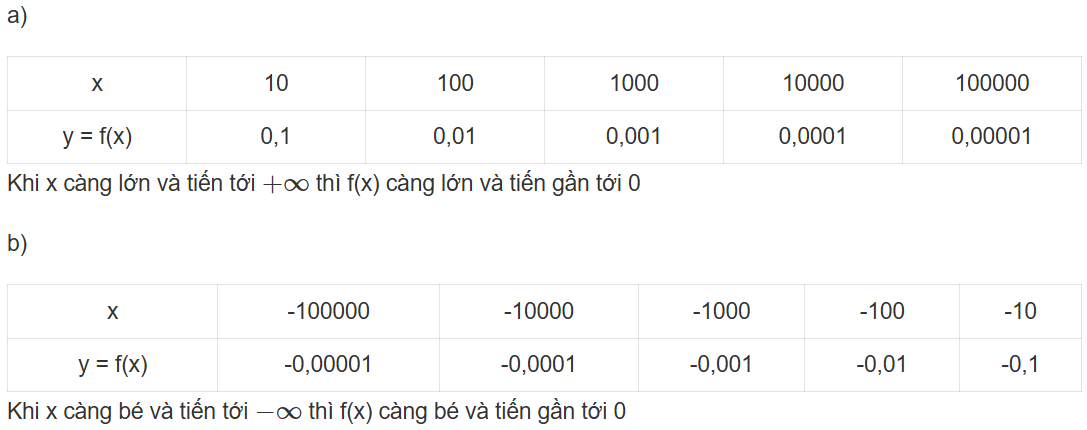
a) Tìm các giá trị còn thiếu trong bảng sau:

Từ đồ thị và bảng trên, nêu nhận xét về giá trị f(x) khi x càng lớn (dần tới +∞)?

b) Tìm các giá trị còn thiếu trong bảng sau: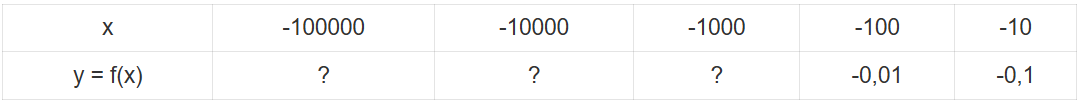 

Từ đồ thị và bảng trên, nêu nhận xét về giá trị f(x) khi x càng bé (dần tới −∞)?

Trả lời:

Thực hành 4: Tìm các giới hạn sau:

a) $\underset{x\to +\infty }{\lim }\frac{1-3x^2}{x^2+2x}$;

b) $\underset{x\to -\infty }{\lim }\frac{2}{x+1}$.

Trả lời:

a) $\underset{x\to +\infty }{\lim }\frac{1-3x^2}{x^2+2x}=\underset{x\to +\infty }{\lim }\frac{\frac{1}{x^2}-3}{1+\frac{2}{x}}=-3$

b) $\underset{x\to -\infty }{\lim }\frac{2}{x+1}=\underset{x\to -\infty }{\lim }\frac{\frac{2}{x}}{1+\frac{1}{x}}=0$.

Vận dụng 1: Một cái hồ đang chứa 200m3 nước mặn với nồng độ 10kg/m3. Người ta ngọt hoá nước trong hồ bằng cách bơm nước ngọt vào hồ với tốc độ 2m3/phút

a) Viết biểu thức C(t) biểu thị nồng độ muối trong hồ sau t phút kể từ khi bắt đầu bơm

b) Tìm giới hạn limt→+∞C(t) và giải thích ý nghĩa

Trả lời:

a) C(t)=10.200200+2t=1000100+t

b) limx→+∞C(t)=limx→+∞2000100+2t=limx→+∞1000t100t+1=limx→+∞1000tlimx→+∞(100t+1)

=limx→+∞1000tlimx→+∞100t+1=00+1=0

Vậy khi t càng lớn và tiến tới +∞ thì nồng độ muối tiến tới 0

5. Giới hạn vô cực của hàm số tại một điểm

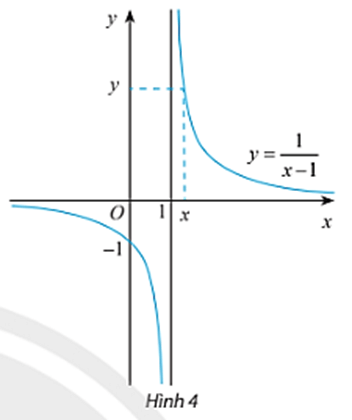
Khám phá 5: Cho hàm số $f\left(x\right)=\frac{1}{x-1}$ có đồ thị như Hình 4.

a) Tìm các giá trị còn thiếu trong bảng sau:

Từ đồ thị và bảng trên, có nhận xét gì về giá trị f(x) khi x dần tới 1 phía bên phải?

b) Tìm các giá trị còn thiếu trong bảng sau:

Từ đồ thị và bảng trên, có nhận xét gì về giá trị f(x) khi x dần tới 1 phía bên trái?

Trả lời:

a) Với x = 1,001 thì y = f(x) = $\frac{1}{x-1}=\frac{1}{1,001-1}=1000$;

Với x = 1,0001 thì y = f(x) = $\frac{1}{x-1}=\frac{1}{1,0001-1}=10000$.

Khi đó ta có bảng:

Nhận xét: Khi x dần tới 1 phía bên phải thì f(x) tăng dần tới một giá trị rất lớn (dương vô cực).

b) Với x = 0,999 thì y = f(x) = $\frac{1}{x-1}=\frac{1}{0,999-1}=-1000$;

Với x = 1,0001 thì y = f(x) = $\frac{1}{x-1}=\frac{1}{0,9999-1}=-10000$.

Khi đó ta có bảng:

Nhận xét: Khi x dần tới 1 phía bên phải thì f(x) giảm dần tới một giá trị rất nhỏ (âm vô cực).

Thực hành 5: Tìm các giới hạn sau:

a) limx→3−2xx−3

b) limx→+∞(3x−1)

Trả lời:

a) limx→3−2xx−3

Ta có: limx→3−2x=2.3=6; limx→3−1x−3=−∞

Do đó: limx→3−2xx−3=limx→3−[2x.1x−3]=−∞

b) Ta có: limx→+∞x=+∞

limx→+∞(3−1x)=3−limx→+∞1x=3−0=3

Do đó: limx→+∞(3x−1)=limx→+∞[x(3−1x)]=+∞

Vận dụng 2: Xét tình huống ở hoạt động khởi động đầu bài học. Gọi x là hoành độ điểm H. Tính diện tích S(x) của hình chữ nhật OHMK theo x. Diện tích này thay đổi như thế nào khi x → 0+ và khi x → +∞.

Trả lời:

Hình chữ nhật OHMK có các kích thước lần lượt là hoành độ và tung độ của điểm M.

Ta có x là hoành độ điểm H nên hoành độ điểm M cũng bằng x và M luôn nằm trên đồ thị $y=\frac{1}{x^2}\left(x>0\right)$ nên tọa độ điểm M là $\left(x;\frac{1}{x^2}\right)\left(x>0\right)$.

Khi đó diện tích hình chữ nhật OHMK là:$x.\frac{1}{x^2}=\frac{1}{x}$.

Khi H gần tiến đến gốc tọa độ nghĩa là x dần tiến đến 0+ thì $\underset{x\to 0^{+}}{\lim }\frac{1}{x}=+\infty$.

Khi H tiến xa sang phía bên phải thì x dần tiến tới +∞ thì $\underset{x\to +\infty }{\lim }\frac{1}{x}=0$.

Bài tập

Bài tập 1: Tìm các giới hạn sau:

a) limx→−2(x2−7x+4)

b) limx→3x−3x2−9

c) limx→13−x+8√x−1

Trả lời:

a) limx→−2(x2−7x+4)

=limx→−2x2−7.limx→−2x+limx→−24

=(−2)2−7.(−2)+4

=22

b) limx→3x−3x2−9

=limx→3x−3(x−3)(x+3)

=limx→31x+3

=13+3

=16

c) limx→13−x+8√x−1

=limx→1(3−x+8√)(3+x+8√)(x−1)(3+x+8√)

=limx→19−x−8(x−1)(3+x+8√)

=limx→11−x(x−1)(3+x+8√)

=limx→1−13+x+8√

=−13+1+8√

=−16

Bài tập 2: Cho hàm số .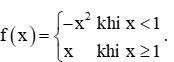

Tìm các giới hạn sau: $\underset{x\to 1^{+}}{\lim }f\left(x\right);\underset{x\to 1^{-}}{\lim }f\left(x\right);\underset{x\to 1}{\lim }f\left(x\right)$ (nếu có).

Trả lời:

+) Với dãy số (xn) bất kì, xn ≤ 1 và xn → 1. Khi đó f(xn) = $-x_n^2$ nên limf(xn) = $\lim \left(-x_n^2\right)=-1$.

Vì vậy $\underset{x\to 1^{-}}{\lim }f\left(x\right)=-1$.

+) Với dãy số (xn) bất kì, xn > 1 và xn → 1. Khi đó f(xn) = xn nên limf(xn) = lim(xn) = 1.

Vì vậy $\underset{x\to 1^{+}}{\lim }f\left(x\right)=1$.

+) Vì $\underset{x\to 1^{+}}{\lim }f\left(x\right)\ne \underset{x\to 1^{-}}{\lim }f\left(x\right)$ nên không tồn tại $\underset{x\to 1}{\lim }f\left(x\right)$.

Bài tập 3: Tìm các giới hạn sau: 

a) limx→+∞4x+32x

b) limx→−∞23x+1

c) limx→+∞x2+1√x+1

Trả lời:

a) limx→+∞4x+32x=limx→+∞4+3x2=4+02=2

b) limx→−∞23x+1=limx→−∞2x3+1x=03+0=0

c) limx→+∞x2+1√x+1=limx→+∞1+1x2√1+1x=1+0√1+0=1

Bài tập 4: Tìm các giới hạn sau:

a) $\underset{x\to -1^{+}}{\lim }\frac{1}{x+1}$;

b) $\underset{x\to -\infty }{\lim }\left(1-x^2\right)$;

c) $\underset{x\to 3^{+}}{\lim }\frac{x}{3-x}$.

Trả lời:

a) $\underset{x\to -1^{+}}{\lim }\frac{1}{x+1}=\underset{x\to -1^{+}}{\lim }\frac{\frac{1}{x}}{1+\frac{1}{x}}=0$;

b) Ta viết: $1-x^2=x^2.\left(\frac{1}{x^2}-1\right)$

Ta có: $\underset{x\to -\infty }{\lim }{x}^2=+\infty ;\underset{x\to -\infty }{\lim }\left(\frac{1}{x^2}-1\right)=-1$

Do đó: $\underset{x\to -\infty }{\lim }\left(1-x^2\right)=\underset{x\to -\infty }{\lim }{x}^2\left(\frac{1}{x^2}-1\right)=-\infty$.

c) Ta viết: $\frac{x}{3-x}=x.\frac{1}{3-x}$

Ta có: $\underset{x\to 3^{+}}{\lim }x=3;\underset{x\to 3^{+}}{\lim }\frac{1}{3-x}=+\infty$

Do đó: $\underset{x\to 3^{+}}{\lim }\frac{x}{3-x}=\underset{x\to 3^{+}}{\lim }\left(x.\frac{1}{3-x}\right)=\underset{x\to 3^{+}}{\lim }x.\underset{x\to 3^{+}}{\lim }\frac{1}{3-x}=+\infty$.

Bài tập 5: Trong hồ có chứa 6000 lít nước ngọt. Người ta bơm nước biển có nồng độ muối là 30 gam/lít vào hồ với tốc độ 15 lít/phút.

a) Chứng tỏ rằng nồng độ muối trong hồ sau t phút kể từ khi bắt đầu bơm là C(t)=30t400+t (gam/lít)

b) Nồng độ muối trong hồ như thế nào nếu t→+∞

Trả lời:

a) Sau thời gian t, số lít nước bơm vào hồ là: 15t (lít)

Trong 15t lít nước biển có lượng muối: 30.15t = 450t (gam)

Nồng độ muối trong hồ sau thời gian t phút: C(t)=450t6000+15t=30t400+t

b) limx→+∞C(t)=limx→+∞30t400+t=limx→+∞30400t+1=300+1=30

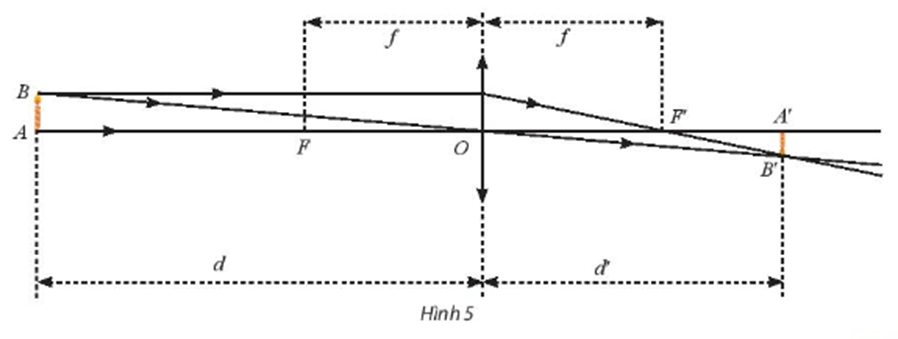
Bài tập 6: Một thấu kính hội tụ có tiêu cự là f > 0 không đổi. Gọi d và d’ lần lượt là khoảng cách từ vật thật và ảnh của nó tới quang tâm O của thấu kính (Hình 5). Ta có công thức $\frac{1}{d}+\frac{1}{d\text{'}}=\frac{1}{f}$ hay $d\text{'}=\frac{df}{d-f}$.

Xét hàm số $g\left(d\right)=\frac{df}{d-f}$. Tìm các giới hạn sau đây và giải thích ý nghĩa.

a) $\underset{d\to f^{+}}{\lim }g\left(d\right)$;

b) $\underset{d\to +\infty }{\lim }g\left(d\right)$.

Trả lời:

a) Ta có: $\underset{d\to f^{+}}{\lim }g\left(d\right)=\underset{d\to f^{+}}{\lim }\frac{df}{d-f}=\underset{d\to f^{+}}{\lim }df.\underset{d\to f^{+}}{\lim }\frac{1}{d-f}=+\infty$.

Như vậy khi khoảng cách của vật đến quang tâm O gần bằng tiêu cự của thấu kính thì khoảng cách từ ảnh đến quang tâm O của thấu kính càng lớn.

b) Ta có: $\underset{d\to +\infty }{\lim }g\left(d\right)=\underset{d\to +\infty }{\lim }\frac{df}{d-f}=\underset{d\to +\infty }{\lim }\frac{f}{1-\frac{f}{d}}=f$.

Như vậy khi khoảng cách của vật đến quang tâm O càng lớn thì khoảng cách từ ảnh đến quang tâm O của thấu kính càng gần tiêu cự.