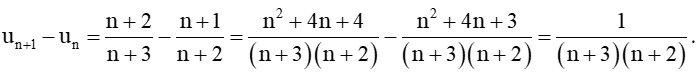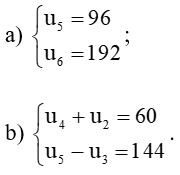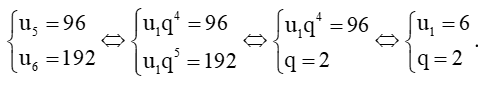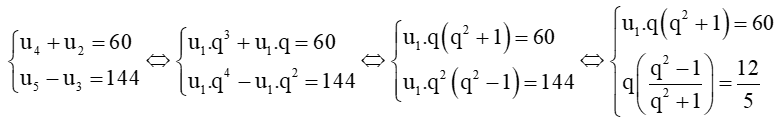Giải SGK Toán 11 Chân trời sáng tạo Bài tập cuối chương II

Bài tập 1: Cho dãy số (u­n) với un = $\frac{n}{3^n-1}$. Ba số hạng đầu tiên của dãy số (un) lần lượt là

A. $\frac{1}{2};\frac{1}{4};\frac{3}{27}$;

B. $\frac{1}{2};\frac{1}{4};\frac{3}{26}$;

C. $\frac{1}{2};\frac{1}{4};\frac{3}{25}$;

D. $\frac{1}{2};\frac{1}{4};\frac{3}{28}$.

Đáp án: B

Giải thích:

Dãy số (u­n) có ba số hạng đầu tiên là:

$u_1=\frac{1}{3^1-1}=\frac{1}{2}$;

$u_2=\frac{2}{3^2-1}=\frac{2}{8}=\frac{1}{4}$;

$u_3=\frac{3}{3^3-1}=\frac{3}{26}$

Bài tập 2: Cho dãy số $\frac{1}{3};\frac{1}{3^2};\frac{1}{3^3};\frac{1}{3^4};\frac{1}{3^5};\mathrm{...}$. Số hạng tổng quát của dãy số này là:

A. $u_n=\frac{1}{3}.\frac{1}{3^{n+1}}$;

B. $u_n=\frac{1}{3^{n+1}}$;

C. $u_n=\frac{1}{3^n}$;

D. $u_n=\frac{1}{3^{n-1}}$.

Đáp án: C

Giải thích: Dãy số $\frac{1}{3};\frac{1}{3^2};\frac{1}{3^3};\frac{1}{3^4};\frac{1}{3^5};\mathrm{...}$ lập thành một cấp số nhân có số hạng đầu là $\frac{1}{3}$ và công bội q = $\frac{1}{3}$, có số hạng tổng quát là: $u_n=\frac{1}{3}.{\left(\frac{1}{3}\right)}^{n-1}={\left(\frac{1}{3}\right)}^n$.

Bài tập 3: Cho dãy số (u­n) với $u_n=\frac{n+1}{n+2}$. Phát biểu nào sau đây là đúng?

A. Dãy số tăng và bị chặn;

B. Dãy số giảm và bị chặn;

C. Dãy số giảm và bị chặn dưới;

D. Dãy số giảm và bị chặn trên.

Đáp án: A

Giải thích:

+) Ta có: $u_{n+1}=\frac{n+1+1}{n+1+2}=\frac{n+2}{n+3}$

Xét hiệu

Vì n ∈ ℕ* nên n > 0, suy ra $\frac{1}{\left(n+3\right)\left(n+2\right)}>0$.

Do đó un+1 > un hay (un) là dãy tăng.

+) Ta có: $u_n=1-\frac{1}{n+2}$

Vì n ∈ ℕ* nên n ≥ 1 suy ra n + 2 ≥ 3

$\Rightarrow u_n=1-\frac{1}{n+2}\ge 1-\frac{1}{3}=\frac{2}{3},\forall n\in N^{\ast }$.

Ta lại có n ∈ ℕ* nên n > 0 suy ra $\frac{1}{n+2}>0$. Do đó $u_n=1-\frac{1}{n+2}<1$.

Vì vậy $\frac{2}{3}\le u_n<1$ nên dãy số (un) bị chặn.

Bài tập 4: Cho cấp số cộng (u­n) có số hạng đầu u1, công sai d. Khi đó, với n ≥ 2 ta có

A. un = u1 + d;

B. un = u1 + (n + 1)d;

C. un = u1 – (n – 1)d;

D. un = u1 + (n – 1)d.

Đáp án: D

Giải thích:

Cấp số cộng (u­n) có số hạng đầu u1, công sai d có số hạng tổng quát là:

un = u1 + (n – 1)d, với n ≥ 2.

Bài tập 5: Cho cấp số cộng (u­n) có u1 = 3 và u2 = – 1. Khi đó

A. u3 = 4;

B. u3 = 2;

C. u3 = – 5;

D. u3 = 7.

Đáp án: C

Giải thích:

Ta có: u2 = u1 + d = – 1

⇔ d = – 1 – u1 = – 1 – 3 = – 4.

Khi đó u3 = u1 + 2d = 3 + 2(– 4) = – 5.

Bài tập 6: Cho cấp số cộng (u­n) có số hạng đầu u1 = – 1 và công sai d = 3. Khi đó S5 bằng

A. 11;

B. 50;

C. 10;

D. 25.

Đáp án: D

Giải thích:

S5=5.[2.(−1)+(5−1).3]2=25

Bài tập 7: Có bao nhiêu số thực x để 2x – 1; x; 2x + 1 theo thứ tự lập thành cấp số nhân?

A. 1;

B. 2;

C. 3;

D. 4.

Đáp án: B

Giải thích:

Do 2x - 1; x; 2x + 1 lần lượt tạo thành cấp số nhân. Gọi công bội là q

Ta có: {x=(2x−1)q2x+1=xq

Suy ra: x2x−1=2x+1x⇔x2=4x2−1

⇔x=3√3 hoặc x=−3√3

Bài tập 8: Một tam giác có số đo các góc lập thành cấp số nhân có công bội q = 2. Số đo các góc của tam giác đó lần lượt là

A. $\frac{\pi }{6};\frac{\pi }{3};\frac{\pi }{2}$;

B. $\frac{\pi }{5};\frac{2\pi }{5};\frac{4\pi }{5}$;

C. $\frac{\pi }{6};\frac{2\pi }{6};\frac{4\pi }{6}$;

D. $\frac{\pi }{7};\frac{2\pi }{7};\frac{4\pi }{7}$.

Đáp án: D

Giải thích:

Giả sử tam giác có số đo các góc theo thứ tự tăng dần lần lượt: x; y; z (rad).

Vì x; y; z lập thành cấp số nhân có công bội q = 2 nên ta có:

y = x.2 = 2x, z = 22.x = 4x.

Mặt khác ta có: x + y + z = π

⇔ x + 2x + 4x = π

⇔ 7x = π

⇔ x = $\frac{\pi }{7}$.

⇒ y = $\frac{2\pi }{7}$ và z = $\frac{4\pi }{7}$.

Bài tập 9: Xét tính tăng, giảm của dãy số (un) với un=3n−12n

Trả lời:

un=3n−12n=(32)n−12n

Ta có: un+1=(32)n+1−12n+1>(32)n−12n=un,∀n∈N∗

Vậy dãy số (un) là dãy số tăng

Bài tập 10: Xét tính bị chặn của dãy số (u­n) với $u_n=\frac{2n+1}{n+2}$.

Trả lời:

Ta có: $u_n=\frac{2n+1}{n+2}=2-\frac{3}{n+2}$

+) Vì n ∈ ℕ* nên n ≥ 1, suy ra n + 2 ≥ 3

$\Rightarrow u_n=2-\frac{3}{n+2}\ge 1$

+) Vì n ∈ ℕ* nên n > 0 suy ra $\frac{3}{n+2}>0$

$\Rightarrow -\frac{3}{n+2}<0$

$\Rightarrow 2-\frac{3}{n+2}<2$

Do đó ta có: $1\le u_n<2$ hay dãy số (un) bị chặn.

Bài tập 11: Tìm số hạng đầu u1 và công sai d của cấp số cộng (un), biết:

a) {5u1+10u5=0S4=14

b) {u7+u15=60u24+u212=1170

Trả lời:

a) {5u1+10u5=0S4=14

⇔{5u1+10u1+40d=04.(2u1+3d)2=14

⇔{15u1+40d=02u1+3d=7

⇔{u1=8d=−3

b) {u7+u15=60u24+u212=1170

⇔{u1+6d+u1+14d=60(u1+3d)2+(u1+11d)2=1170

⇔{2u1+20d=60(u1+3d)2+(u1+11d)2=1170

⇔{u1=30−10d(u1+3d)2+(u1+11d)2=1170

Suy ra: (30−10d+3d)2+(30−10d+11d)2=1170

⇔900−420d+49d2+900+60d+d2=1170

⇔50d2−360d+630=0

⇔d=3 hoặc d=215

Với d=3 thì u1=0

Với d=215 thì u1=−12

Bài tập 12: Tìm số hạng đầu u1 và công bội q của cấp số nhân (un), biết:

Trả lời:

a) 

Vậy cấp số nhân (un) có số hạng đầu u1 = 6 và công bội q = 2.

b) 

Xét $q\left(\frac{q^2-1}{q^2+1}\right)=\frac{12}{5}$

⇔ 5(q3 – q) = 12(q2 + 1)

⇔ 5q3 – 12q2 – 5q – 12 = 0

⇔ (q – 3)(5q2 + 3q + 4) = 0

⇔ q = 3 (do 5q2 + 3q + 4 = 0 vô nghiệm)

⇒ u1 = 2.

Vậy cấp số nhân (un­) có số hạng đầu u1 = 2 và công bội q = 3.

Bài tập 13: Giả sử một quần thể động vật ở thời điểm ban đầu có 110 000 cá thể, quần thể này có tỉ lệ sinh là 12%/năm, xuất cư là 2%/năm, tử vong là 8%/năm. Dự đoán số cá thể của quần thể đó sau hai năm.

Trả lời:

- Số cá thể của quần thể qua các năm tạo thành cấp số nhân có công bội là: q = 1 + 0,12 - 0,02 - 0,08 = 1,02

- Số cá thể sau hai năm là: 110000.1,022=114444 (cá thể)

Bài tập 14: Một cây đàn organ có tần số âm thanh các phím liên tiếp tạo thành một cấp số nhân. Cho biết tần số phím La Trung là 400Hz và tần số phím La Cao cao hơn 12 phím là 800 Hz (nguồn: https://vi.wikipedia.org/wiki/Organ ). Tìm công bội của cấp số nhân nói trên (làm tròn kết quả đến hàng phần nghìn).

Trả lời:

Ta có tần số âm thanh các phím liên tiếp tạo thành một cấp số nhân (un).

Đặt tần số âm thanh của phím La Trung là số hạng đầu u1 = 400.

Phím La Cao cao hơn 12 phím so với phím La Trung nên phím này ở u13 = 800.

Ta lại có: u13 = u1.q12 = 400q12 = 800 ⇔ q = 

Vậy công bội của cấp số nhân trên là 1,059.

Bài tập 15: Dân số Việt Nam năm 2020 là khoảng 97,6 triệu người (theo Niên giảm thống kê năm 2020). Nếu trung bình mỗi năm tăng 1,14% thì ước tính dân số Việt Nam năm 2040 là khoảng bao nhiêu người (làm tròn kết quả đến hàng trăm nghìn)

Trả lời:

- Ước tính dân số Việt Nam năm 2040 là: 97,6.(1+0,0114)20=122,4(triệu người)