Giải SGK Toán 11 Chân trời sáng tạo Bài 3: Cấp số nhân - Giải SGK Toán 11 - Chân trời sáng tạo

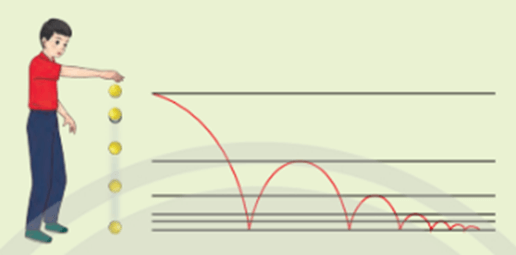
Hoạt động khởi động: Một quả bóng rơi từ một vị trí có động cao 120 cm. Khi chạm đất, nó luôn nảy lên với độ cao bằng một nửa độ cao của lần rơi trước đó.

Gọi u1 = 120 là độ cao của lần rơi đầu tiên và u2; u3; u4; ...; un; ... là độ cao của các lần rơi kế tiếp. Tìm 5 số hạng đầu tiên của dãy (un) và tìm điểm đặc biệt của dãy số đó.

Hoạt động khởi động trang 57 Toán 11 Tập 1 Chân trời sáng tạo | Giải Toán 11

Trả lời:

Ta có: $u_{1} = 120$

Vì độ cao sau bằng một nửa độ cao của lần rơi trước đó nên ta có:

$u_{2} = \frac{1}{2} u_{1} = \frac{1}{2} .120 = 60$ ;

$u_{3} = \frac{1}{2} u_{2} = \frac{1}{2} .60 = 30$ ;

$u_{4} = \frac{1}{2} u_{3} = \frac{1}{2} .30 = 15$ ;

$u_{5} = \frac{1}{2} u_{4} = \frac{1}{2} .15 = 7, 5$ .

Điểm đặc biệt của dãy số là:

Dãy số giảm dần và mỗi số hạng sau đều bằng tích của số hạng ngay trước nó với một số q không đổi là $q = \frac{1}{2}$ .

1. Cấp số nhân

Khám phá 1:

a) Tìm thương của hai số hạng liên tiếp trong dãy: 2; 4; 8; 16; 32; 64

b) Tìm điểm giống nhau của các dãy số sau:

i) 3; 6; 12; 24; 48

ii) 1;12;14;18;116

iii) 2; -6; 18; -54; 163; -486

Trả lời:

a) Thương của 2 số hạng liên tiếp trong dãy là 2

b) Điểm giống nhau của các dãy số là: mỗi số hạng đều bằng tích của số hạng liền trước với một số không đổi

Thực hành 1: Cho ba số tự nhiên m, n, p theo thứ tự lập thành cấp số cộng. Chứng minh ba số 2m, 2n, 2p theo thứ tự lập thành cấp số nhân.

Trả lời:

Vì m, n, p theo thứ tự lập thành cấp số cộng nên n = m = p – n = d.

Ta có: 2n : 2m = 2n – m = 2d; 2p : 2n = 2p – n = 2d

Do đó 2n : 2m = 2p : 2n nên đây là một cấp số nhân với công bội q = 2d.

Vận dụng 1: Một quốc gia có dân số năm 2011 là P triệu người. Trong 10 năm tiếp theo, mỗi năm dân số tăng a%. Chứng minh rằng dân số các năm từ 2011 đến năm 2021 của quốc gia đó tạo thành cấp số nhân. Tìm công bội của cấp số nhân này.

Trả lời:

Dân số qua các năm là:

u2011=P

u2012=P+aP=P(1+a)=u2011.(1+a)

u2013=P(1+a)+aP(1+a)=P(1+a)2=u2012.(1+a)

.....

un+1=un(1+a)

Vậy dân số các năm tạo thành cấp số nhân có công bội là 1+a

Vận dụng 2: Tần số của ba phím liên tiếp Sol, La, Si trên một cây đàn organ tạo thành cấp số nhân. Biết tần số của hai phím Sol và Si lần lượt là 415 Hz và 466 Hz (theo https:..vi.wikipedia.org/wiki/Đô_(nốt nhạc)). Tính tần số của phím La (làm tròn đến hàng đơn vị).

Vận dụng 2 trang 58 Toán 11 Tập 1 Chân trời sáng tạo | Giải Toán 11

Trả lời:

- Vì tần số của ba phím liên tiếp Sol, La, Si tạo thành một cấp số nhân nên ta có tần số của phím La bằng: $\sqrt{415.466} \approx 440$ .

2. Số hạng tổng quát của cấp số nhân

Khám phá 2: Cho cấp số nhân (un) có công bội q. Tính u2,u3,u4 và u10 theo u1 và q

Trả lời:

u2=u1.q

u3=u2.q=u1.q2

u4=u3.q=u1.q3

u10=u1.q9

Thực hành 2: Viết công thức số hạng tổng quát un theo số hạng đầu u1 và công bội q của các cấp số nhân sau:

a) 5; 10; 20; 40; 80; ...

b) $1; \frac{1}{10}; \frac{1}{100}; \frac{1}{1 000}; \frac{1}{10 000}; ...$

Trả lời:

a) Cấp số nhân 5; 10; 20; 40; 80; ... có số hạng đầu u1 = 5 và công bội q = 2.

Khi đó công thức số hạng tổng quát:

un = u1.qn-1 = 5.2n-1.

b) Cấp số nhân $1; \frac{1}{10}; \frac{1}{100}; \frac{1}{1 000}; \frac{1}{10 000}; ...$ có số hạng đầu u1 = 1 và công bội $q = \frac{1}{10}$ . Khi đó công thức số hạng tổng quát:

$u_{n} = 1. {(\frac{1}{10})}^{n - 1} = {(\frac{1}{10})}^{n - 1}$ .

Vận dụng 3: Chu kì bán rã của nguyên tố phóng xạ poloni 210 là 138 ngày, nghĩa là sau 138 ngày, khối lượng của nguyên tố đó chỉ còn một nửa. Tính khối lượng còn lại của 20 gam poloni 210 sau:

a) 690 ngày

b) 7314 ngày (khoảng 20 năm)

Trả lời:

a) Sau 690 = 138.5 ngày, tức là sau 5 chu kì bán rã, khối lượng nguyên tố Poloni còn lại là:

20.(12)4=1,25 (gam)

b) Sau 7314 = 138.53 ngày, tức là sau 53 chu kì bán rã, khối lượng nguyên tố Poloni còn lại là:

20.(12)52=4,44.10−15 (gam)

3. Tổng của n số hạng đầu tiên của cấp số nhân

Khám phá 3: Cho cấp số nhân (un) có công bội q. Đặt Sn = u1 + u2 + ... + un.

a) So sánh q.Sn và (u2 + u3 + ... + un) + q.un;

b) So sánh u1 + q.Sn và Sn + u1.qn.

Trả lời:

a) Ta có: Snq = (u1 + u2 + ... + un).q = u1q + u2q + u3q + ... + un-1q + unq

= u2 + u3 + u4 + ... + un + unq

= (u2 + u3 + ... + un) + q.un

Vậy q.Sn = (u2 + u3 + ... + un) + q.un.

b) Ta có: u1 + q.Sn = u1 + q.(u1 + u2 + ... + un) = u1 + u1q + u2q + u3q + ... + un-1q + unq

= u1 + u2 + ... + un + unq = = Sn + u1qn-1.q = Sn + u1qn.

Vậy u1 + q.Sn = Sn + u1.qn.

Thực hành 3: Tính tổng n số hạng đầu tiên của cấp số nhân (un) trong các trường hợp sau:

a) u1=105;q=0,1;n=5

b) u1=105;u2=−20;n=5

Trả lời:

a) S5=105.(1−0,15)1−0,1=11110

b) u2=−20=u1.q. Suy ra q=−2

S5=10.(1−(−2)5)1−(−2)=110

Vận dụng 4: Trong bài toán ở hoạt động khởi động đầu bài học, tính tổng các độ cao của quả bóng sau 10 lần rơi đầu tiên.

Trả lời:

Dãy số đã cho là một cấp số nhân với số hạng đầu u1 = 120 và công sai $q = \frac{1}{2}$ .

Khi đó công thức số hạng tổng quát của cấp số nhân này là: un = 120. ${(\frac{1}{2})}^{n - 1}$ .

Độ cao của quả bóng sau lần rơi thứ 10 là u10 = 120. ${(\frac{1}{2})}^{10 - 1}$ = $\frac{15}{64}$ .

Tổng độ cao của quả bóng sau 10 lần rơi đầu tiên là:

$S_{10} = \frac{10 (120 + \frac{15}{64})}{2} \approx 601, 2$ .

Bài tập

Bài tập 1: Trong các dãy số sau, dãy số nào là cấp số nhân?

a) un=3(−2)n

b) un=(−1)n+1.7n

c) {un=1un+1=2un+3

Trả lời:

a) un=3(−2)n=(−6).(−2)n

Vậy dãy trên là cấp số nhân có công bội là -2

b) un=(−1)n+1.7n=7.(−7)n−1

Vậy dãy trên là cấp số nhân có công bội là -7

c) {un=1un+1=2un+3

Dãy trên không phải cấp số nhân

Bài tập 2: Tìm số hạng đầu và công bội của cấp số nhân (un) biết:

a) {u5−u1=15u4−u2=6

b) {u1−u3+u5=65u1+u7=325

Trả lời:

a) {u5−u1=15u4−u2=6

⇔{u1.q4−u1=15u1.q3−u1.q=6

⇔{q=2u1=1

b) {u1−u3+u5=65u1+u7=325

⇔{u1−u1.q2+u1.q4=65u1+u1.q6=325

⇔{q=2u1=5

Bài tập 3:

a) Số đo bốn góc của một tứ giác lập thành cấp số nhân. Tìm số đo của bốn góc đó biết rằng số đo của góc lớn nhất gấp 8 lần số đo của góc nhỏ nhất.

b) Viết sáu số xen giữa các số – 2 và 256 để được cấp số nhân có tám số hạng. Nếu viết tiếp số hạng thứ 15 là bao nhiêu?

Trả lời:

a) Gọi số đo bốn góc của một tứ giác được lập thành một cấp số nhân có công bội q theo thứ tự từ bé đến lớn là: α; β; γ; φ.

Ta có: β = αq, γ = α.q2, φ = α.q3.

Ta lại có: φ = 8α nên q3 = 8 ⇔ q = 2.

Do đó cấp số cộng trên trở thành: α; 2α; 4α; 8α.

Tổng bốn góc trong tứ giác bằng 360° nên α + 2α + 4α + 8α = 360°

⇔ 15α = 360°

⇔ α = 24°

Vậy số đo của các góc trong tứ giác lần lượt là 24°; 48°; 72°; 96°.

b) Cấp số nhân đã cho có u1 = – 2 và u8 = 256.

Ta có: u8 = u1q7 = (– 2).q7 = 256

⇔ q = – 2

Suy ra các số hạng xen giữa hai số – 2 và 256 là: 4; – 8; 16; – 32; 64; – 128.

Số hạng thứ 15 của dãy là: u15 = (– 2).( – 2)14 = (– 2)15 = 0 – 32 768.

Bài tập 4: Ba số 2b−a,1b,2b−c theo thứ tự lập thành cấp số cộng. Chứng minh rằng ba số a, b, c theo thứ tự lập thành cấp số nhân

Trả lời:

a) Vì ba số 2b−a,1b,2b−c theo thứ tự lập thành cấp số cộng nên ta có:

1b=2b−a+d⇔b−a=2b+db(b−a)⇔(bd−1)a=(bd+1)b⇔bd+1bd−1=ab

2b−c=1b+d⇔2b=b−c+qb(b−c)⇔(1+bd)c=b(bd−1)⇔bd+1bd−1=bc

Suy ra: ab=bc

Gọi b = a.q

Ta có: aaq=aqc⇔c=aq2⇔c=bq

Vậy a,b,c lần lượt là cấp số nhân có công bội là q

Bài tập 5: Tính các tổng sau:

a) Sn=1+13+132+...+13n

b) Sn=9+99+999+...+999...9 (n chữ số 9)

Trả lời:

Dãy số $1; \frac{1}{3}; \frac{1}{3^{2}}; ...; \frac{1}{3^{n}}$ lập thành một cấp số nhân có số hạng đầu u1 = 1 và công bội q = $\frac{1}{3}$ .

Khi đó tổng của n số hạng đầu của cấp số nhân là:

$S_{n} = \frac{n (1 + \frac{1}{3^{n}})}{2} = \frac{(3^{n} + 1) n}{{2.3}^{n}}$ .

Bài tập 6: Một loại vị khuẩn được nuôi cấy trong phòng thí nghiệm, cứ mỗi phút số lượng lại tăng lên gấp đôi số lượng đang có. Từ một vi khuẩn ban đầu, hãy tính tổng số vi khuẩn có trong ống nghiệm sau 20 phút.

Trả lời:

Tổng số vi khuẩn có trong ống nghiệm sau 20 phút là:

S20=20.[1−220]1−2=20971500

Bài tập 7: Giả sử một thành phố có dân số năm 2022 là khoảng 2,1 triệu người và tốc độ gia tăng dân số trung bình mỗi năm là 0,75%.

a) Dự đoán dân số của thành phố đó vào năm 2032.

b) Nếu tốc độ gia tăng dân số vẫn giữ nguyên như trên thì ước tính vào năm nào dân số của thành phố đó sẽ tăng gấp đôi so với năm 2022?

Trả lời:

Số dân của thành phố qua các năm với tốc độ gia tăng dân số trung bình mỗi năm là 0,75% lập thành một cấp số nhân (un) với số hạng đầu là u1 = 2,1 (ở năm 2022) và công bội q = 1 + 0,75% = 1,0075 có số hạng tổng quát là: un = 2,1.(1,0075)n-1.

a) Dự đoán dân số của thành phố vào năm 2032 là:

u11 = 2,1.(1,0075)10 ≈ 2,3 triệu người.

b) Dân số của năm thứ n (so với năm 2022) là: 2.2,1 = 4,2 (triệu người).

Ta có: un = 2,1.(1,0075)n-1 = 4,2

⇒ n – 1 ≈ 93

Vậy ước tính vào năm 2022 + 93 = 2115 thì dân số thành phố đó gấp đôi so với năm 2022.

Bài tập 8: Trong trò chơi mạo hiểm nhảy bungee, mỗi lần nhảy, người chơi sẽ được dây ăn toàn có tính đàn hồi kéo nảy ngược lên 60% chiều sâu của cú nhảy. Một người chơi bungee thực hiện cú nhảy đầu tiên có độ cao nảy ngược lên là 9m

a) Tính độ cao nảy ngược lên của người đó ở lần nảy thứ ba

b) Tính tổng các độ cao nảy ngược lên của người đó trong 5 lần đầu

Trả lời:

Độ cao nảy ngược lên của người đó ở lần nảy thứ nhất là u1=9

Độ cao các lần nảy lần lượt tạo thành cấp số nhân có công bội là q = 0,6

un=9.0,6n−1

a) u3=9.0,63−1=3,24

b) S5=9.[1−0,65]1−0,6=20,75