Giải SGK Toán 11 Chân trời sáng tạo Bài tập cuối chương III

Bài tập 1: lim$\frac{n+3}{n^2}$ bằng:

A. 1;

B. 0;

C. 3;

D. 2.

Đáp án: B

Giải thích: Ta có: $\lim \frac{n+3}{n^2}=\lim \frac{\frac{1}{n}+\frac{3}{n^2}}{1}=0$.

Bài tập 2: Tổng của cấp số nhân lùi vô hạn:

$M=1+\frac{1}{4}+\frac{1}{4^2}+\mathrm{...}+\frac{1}{4^n}+\mathrm{...}$ bằng:

A. $\frac{3}{4}$;

B. $\frac{5}{4}$;

C. $\frac{4}{3}$;

D. $\frac{6}{5}$.

Đáp án: C

Giải thích:

M=11−14=43

Bài tập 3: $\underset{x\to 3}{\lim }\frac{x^2-9}{x-3}$ bằng

A. 0;

B. 6;

C. 3;

D. 1.

Đáp án: B

Giải thích: Ta có: $\underset{x\to 3}{\lim }\frac{x^2-9}{x-3}=\underset{x\to 3}{\lim }\frac{\left(x+3\right)\left(x-3\right)}{x-3}=\underset{x\to 3}{\lim }\left(x+3\right)=6$.

Bài tập 4: Hàm số: f(x) = 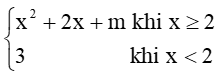 liên tục tại x = 2 khi

A. m = 3

B. m = 5

C. m = -3

D. m = -5

Đáp án: D

Giải thích:

limx→2+f(x)=limx→2+(x2+2x+m)=22+2.2+m=m+8

limx→2−f(x)=limx→2−3=3

Để hàm số f(x) liên tục tại x = 2 thì m + 8 = 3 Hay m = -5

Bài tập 5: $\underset{x\to +\infty }{\lim }\frac{2x-1}{x}$ bằng

A. 2;

B. – 1;

C. 0;

D. 1.

Đáp án: A

Giải thích: Ta có: $\underset{x\to +\infty }{\lim }\frac{2x-1}{x}=\underset{x\to +\infty }{\lim }\frac{2-\frac{1}{x}}{1}=2$.

Bài tập 6: Tìm các giới hạn sau:

a) lim3n−1n

b) limn2+2√n

c) lim23n+1

d) lim(n+1)(2n+2)n2

Trả lời:

a) lim3n−1n=lim(3−1n)=3−lim1n=3−0=3

b) limn2+2√n=limn2+2n2−−−−√=lim1+1n2−−−−−√=1+lim1n2−−−−−−−−√=1+0−−−−√=1

c) lim23n+1=lim2n3+1n=lim2n3+lim1n=03+0=0

d) lim(n+1)(2n+2)n2=lim2n2+4n+2n2=lim(2+4n+2n2)

=2+lim4n+lim2n2=2+0+0=2

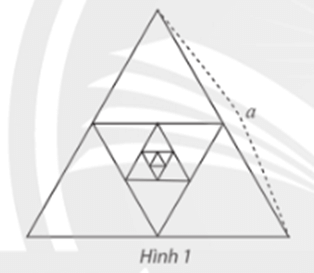
Bài tập 7: Cho tam giác đều có cạnh bằng a, gọi là tam giác H1. Nỗi các trung điểm của H1 để tạo thành tam giác H2. Tiếp theo, nối các trung điểm của H2 để tạo thành tam giác H3 (Hình 1). Cứ tiếp tục như vậy, nhận được dãy tam giác H1, H2, H3, ...

Tỉnh tổng chu vi và tổng diện tích của các tam giác của dãy.

Trả lời:

Ta có:

Diện tích tam giác H1 = S và chu vi tam giác H1 = 3a;

Diện tích tam giác H2 = $\frac{1}{4}$S và chu vi tam giác H2 = $\frac{1}{2}$3a;

Diện tích tam giác H2 = ${\left(\frac{1}{4}\right)}^2$S và chu vi tam giác H3 = ${\left(\frac{1}{2}\right)}^2$3a;

...

Diện tích tam giác Hn = ${\left(\frac{1}{4}\right)}^{n-1}$S và chu vi tam giác H2 = ${\left(\frac{1}{2}\right)}^{n-1}$3a;

Khi đó:

Diện tích của dãy các tam giác H1; H2; H3; ...; H4 lập thành một cấp số nhân lùi vô hạn có số hạng đầu tiên u1 = S và công bội q = $\frac{1}{4}$ có tổng bằng $S+\frac{1}{4}S+{\left(\frac{1}{4}\right)}^{2}S+\mathrm{...}+{\left(\frac{1}{4}\right)}^{n-1}S+\mathrm{...}=\frac{S}{1-\frac{1}{4}}=\frac{4}{3}S$.

Diện tích của dãy các tam giác H1; H2; H3; ...; H4 lập thành một cấp số nhân lùi vô hạn có số hạng đầu tiên u1 = 3a và công bội q = $\frac{1}{2}$ có tổng bằng

$3a+\frac{1}{2}.3a+{\left(\frac{1}{2}\right)}^2.3a+{\left(\frac{1}{2}\right)}^3.3a+\mathrm{...}+{\left(\frac{1}{2}\right)}^{n-1}3a+\mathrm{...}=\frac{3a}{1-\frac{1}{2}}=6a$.

Bài tập 8: Tìm các giới hạn sau:

a) limx→−1(3x2−x+2)

b) limx→4x2−16x−4

c) limx→23−x+7√x−2

Trả lời:

a) limx→−1(3x2−x+2)=3.(−1)2−(−1)+2=6

b) limx→4x2−16x−4=limx→4(x−4)(x+4)x−4=limx→4(x+4)=4+4=8

c) limx→23−x+7√x−2=limx→2(3−x+7√)(3+x+7√)(x−2)(3+x+7√)

=limx→29−x−7(x−2)(3+x+7√)=limx→2−13+x+7√=−13+2+7√=−16

Bài tập 9: Tìm các giới hạn sau:

a) $\underset{x\to +\infty }{\lim }\frac{-x+2}{x+1}$;

b) $\underset{x\to -\infty }{\lim }\frac{x-2}{x^2}$.

Trả lời:

a) $\underset{x\to +\infty }{\lim }\frac{-x+2}{x+1}=\underset{x\to +\infty }{\lim }\frac{-1+\frac{2}{x}}{1+\frac{1}{x}}=-1$.

b) $\underset{x\to -\infty }{\lim }\frac{x-2}{x^2}=\underset{x\to -\infty }{\lim }\frac{\frac{1}{x}-\frac{2}{x^2}}{1}=0$.

Bài tập 10: Tìm các giới hạn sau:

a) limx→4+1x−4

b) limx→2+x2−x

Trả lời:

a) limx→4+1x−4=+∞

b) limx→2+x2−x=−∞

Bài tập 11: Xét tính liên tục của hàm số f(x) = .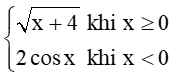

Trả lời:

+) Với x ∈ (0; + ∞) ta có f(x) = $\sqrt{x+4}$ liên tục.

+) Với x ∈ (– ∞; 0) ta có f(x) = 2cosx liên tục.

+) Tại x = 0, ta có:

$\underset{x\to 0^{+}}{\lim }f\left(x\right)=\underset{x\to 0^{+}}{\lim }\sqrt{x+4}=2$;

$\underset{x\to 0^{-}}{\lim }f\left(x\right)=\underset{x\to 0^{-}}{\lim }\left(2\cos x\right)=2$.

Suy ra $\underset{x\to 0}{\lim }f\left(x\right)=\underset{x\to 0^{+}}{\lim }f\left(x\right)=\underset{x\to 0^{-}}{\lim }f\left(x\right)=2=f\left(0\right)$

Do đó hàm số liên tục tại x = 0.

Vậy hàm số liên tục trên ℝ.

Bài tập 12: Cho hàm số f(x) = 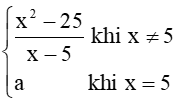. Tìm a để hàm số y = f(x) liên tục trên ℝ.

Trả lời:

Khi x≠5: f(x)=x2−25x−5 là hàm phân thức nên f(x) liên tục trên các khoảng (−∞;5)∪(5;+∞)

Để f(x) liên tục trên R thì f(x) liên tục tại x = 5. Hay limx→5f(x)=f(5)

limx→5f(x)=limx→5x2−25x−5=limx→5(x−5)(x+5)x−5=limx→5(x+5)=5+5=10

f(5) = a

Suy ra: a = 10

Bài tập 13: Trong một tủ thí nghiệm, nhiệt độ trong tủ sấy được điều khiển tăng từ 10°C, mỗi phút tăng 2°C trong 60 phút, sau đó giảm mỗi phút 3°C trong 40 phút. Hàm số biểu thị nhiệt độ (tính theo ºC) trong tủ theo thời gian t (tính theo phút) có dạng

T(t) = 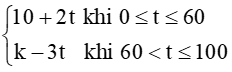 (k là hằng số).

Biết rằng T(t) là hàm liên tục trên tập xác đinh. Tìm giá trị của k.

Trả lời:

+) Với 0 ≤ t < 60 thì T(t) = 10 + 2t là hàm số liên tục.

+) Với 60 < t ≤ 100 thì T(t) = k – 3t là hàm số liên tục.

+) Tại t = 60, ta có:

$\underset{t\to {60}^{-}}{\lim }T\left(t\right)=\underset{t\to {60}^{-}}{\lim }\left(10+2t\right)=130$

$\underset{t\to {60}^{+}}{\lim }T\left(t\right)=\underset{t\to {60}^{-}}{\lim }\left(k-3t\right)=k-180$

Để hàm số liên tục trên tập xác định [0; 100] thì hàm số liên tục tại x = 60

⇔ k – 180 = 130

⇔ k = 240.