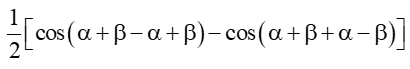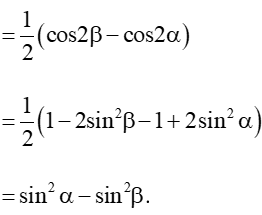Giải SGK Toán 11 Chân trời sáng tạo Bài tập cuối chương I

Bài tập 1: Góc lượng giác nào tương ứng với chuyển động quay $3\frac{1}{5}$ vòng ngược chiều kim đồng hồ?

A. $\frac{16\pi }{5}$;

B. ${\left(\frac{16}{5}\right)}^o$;

C. 1 152°;

D. 1 152π.

Đáp án: C

Giải thích: 1 vòng tròn tương ứng với 2π hay 360o. Vậy 315 vòng là góc 1152o

Bài tập 2: Trong trường hợp nào dưới đây cosα = cosβ và sinα = – sinβ ?

A. β = – α;

B. β = π – α;

C. β = π + α;

D. $\beta =\frac{\pi }{2}+\alpha$.

Đáp án: A

Giải thích: 

+) Xét β = – α, khi đó:

cosβ = cos(– α) = cosα;

sinβ = sin(– α) = sinα hay sinα = – sinβ .

Do đó A thỏa mãn.

+) Xét β = π – α, khi đó:

cosβ = cos(π – α) = – cosα;

sinβ = sin(π – α) = sinα.

Do đó B không thỏa mãn.

+) Xét β = π + α, khi đó:

cosβ = cos(π + α) = – cosα;

sinβ = sin(π + α) = – sinα.

Do đó C không thỏa mãn.

+) Xét $\beta =\frac{\pi }{2}+\alpha$, khi đó:

cosβ = cos($\frac{\pi }{2}+\alpha$) = – sinα;

sinβ = sin($\frac{\pi }{2}+\alpha$) = cosα.

Do đó D không thỏa mãn.

Bài tập 3: Khẳng định nào sau đây đúng?

A. Hàm số y = sinx là hàm số chẵn;

B. Hàm số y = cosx là hàm số chẵn;

C. Hàm số y = tanx là hàm số chẵn;

D. Hàm số y = cotx là hàm số chẵn.

Đáp án: B

Giải thích: 

Ta có tập xác định của hàm số y = cosx là ℝ.

Nếu với x ∈ ℝ thì – x ∈ ℝ và y(– x) = cos(– x) = cosx = y(x).

Vậy hàm số y = cosx là hàm số chẵn.

Bài tập 4: Nghiệm âm lớn nhất của phương trình lượng giác cos2x = cos$\left(x+\frac{\pi }{3}\right)$ là

A. $-\frac{\pi }{9}$;

B. $-\frac{5\pi }{3}$;

C. $-\frac{7\pi }{9}$;

D. $-\frac{13\pi }{9}$.

Đáp án: A

cos2x=cos(x+π3)

⇔2x=x+π3+k2π,k∈Z hoặc 2x=−x−π3+k2π,k∈Z

⇔x=π3+k2π,k∈Z hoặc x=−π9+k2π3,k∈Z

Nghiệm âm lớn nhất của phương trình là x=−π9

Bài tập 5: Số nghiệm của phương trình tanx = 3 trong khoảng $\left(-\frac{\pi }{2};\frac{7\pi }{3}\right)$ là

A. 1;

B. 2;

C. 3;

D. 4.

Đáp án: B

Giải thích: 

Xét phương trình tanx = 3

⇔ x ≈ 1,25 + kπ, k ∈ ℤ

Xét: $-\frac{\pi }{2}<x<\frac{7\pi }{3}\iff -\frac{\pi }{2}<1,25+k\pi <\frac{7\pi }{3}\iff$ -0,9 < k < 1,94.

Mà k ∈ ℤ nên k ∈ {0; 1}.

Vậy có 2 nghiệm của phương trình đã cho nằm trong khoảng $\left(-\frac{\pi }{2};\frac{7\pi }{3}\right)$.

Bài tập 6: Nhiệt độ ngoài trời ở một thành phố vào các thời điểm khác nhau trong ngày có thể được mô phỏng bởi công thức h(t) = 29 + 3sin$\frac{\pi }{12}$(t-9), với h được tính bằng độ C và t là thời gian trong ngày tính bằng giờ. Nhiệt độ thấp nhất trong ngày là bao nhiêu độ C và vào lúc mấy giờ

(Theo https://www.sciencedirect.com/science/article/abs/pii/0168192385900139)

A. 32°C, lúc 15 giờ;

B. 29°C, lúc 9 giờ;

C. 26°C, lúc 3 giờ;

D. 26°C, lúc 0 giờ;

Đáp án: C

Giải thích: 

Với mọi t, ta có: sinπ12(t−9)≥−1  

Suy ra: 29+3sinπ12(t−9)≥26  

Nhiệt độ thấp nhất trong ngày là 26o, xảy ra khi sinπ12(t−9)=−1  

⇔π12(t−9)=−π2+k2π,k∈Z

⇔t=3+24k,k∈Z

Do t là thời gian trong ngày tính bằng giờ nên 0≤t≤24. Suy ra: t = 3

Bài tập 7: Một chiếc quạt trần năm cánh quay với tốc độ 45 vòng trong một phút. Chọn chiều quay của quạt là chiều thuận. Sau 3 giây, quạt quay được một góc có số đo bao nhiêu radian?

Trả lời:

Tốc độ góc của quạt trần là: $\frac{45.2\pi }{60}=\frac{3\pi }{2}$(rad/s).

Sau 3 giây, quạt quay được một góc có số đo là: $\frac{3\pi }{2}.3=\frac{9\pi }{2}$rad.

Bài tập 8: Cho cosα = $\frac{1}{3}$ và $-\frac{\pi }{2}<\alpha <0$. Tính:

a) sinα;

b) sin2α;

c) cos$\left(\alpha +\frac{\pi }{3}\right)$.

Trả lời:

a) Do −π2<α<0 nên sinα<0

sinα=−1−cos2α−−−−−−−−√=−22√3

b) sin2α=2sinα.cos=2−22√3.13=−42√9

c) cos(α+π3)=cosα.cosπ3−sinα.sinπ3

cos(α+π3)=13.12−−22√3.3√2=1+26√6

Bài tập 9: Chứng minh đẳng thức lượng giác:

a) sin(α + β)sin(α – β) = sin2α – sin2β;

b) cos4α – cos4$\left(\alpha -\frac{\pi }{2}\right)$ = cos2α.

Trả lời:

a) sin(α + β)sin(α – β) = sin2α – sin2β

Ta có: sin(α + β)sin(α – β) =

b) Ta có: cos4α – cos4$\left(\alpha -\frac{\pi }{2}\right)$ = cos4α – sin4α = (cos2α – sin2α)(cos2α + sin2α)

= cos2α – sin2α = cos2α.