Giải SGK Toán 11 Chân trời sáng tạo Bài 4: Hàm số lượng giác và đồ thị

Hoạt động khởi động: Vì sao mặt cắt của sóng nước trên mặt hồ được gọi là có dạng hình sin?

Trả lời:

- Vì hình ảnh mặt cắt sóng nước giống với đồ thị của hàm lượng giác y = sinx

1. Hàm số lượng giác

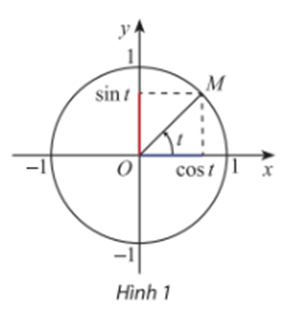
Khám phá 1: Cho số thực t và M là điểm biểu diễn của góc lượng giác có số đo t rad trên đường tròn lượng giác, hãy giải thích vì sao xác định duy nhất:

a) Giá trị sint và cost;

b) Giá trị tant (nếu $t\ne \frac{\pi }{2}+k\pi ,k\in Z$) và cost (nếu $t\ne k\pi ,k\in Z$).

Trả lời:

Trên đường tròn lượng giác, điểm M là điểm biểu diễn góc lượng giác có số đo t, khi đó:

- Tung độ của điểm M là sint.

- Hoành độ của điểm M là cost.

Vì tung độ và hoành độ của điểm M là xác định duy nhất nên sint và cost xác định duy nhất.

b) Nếu $t\ne \frac{\pi }{2}+k\pi ,k\in Z$ thì tan t = $\frac{\sin t}{\text{cos}t}$ xác định duy nhất vì sint và cost xác định duy nhất.

Nếu t$\ne$k$\pi$ thì cot t = $\frac{\text{cos}t}{\sin t}$ xác định duy nhất vì sint và cost xác định duy nhất.

2. Hàm số chẵn, hàm số lẻ, hàm số tuần hoàn

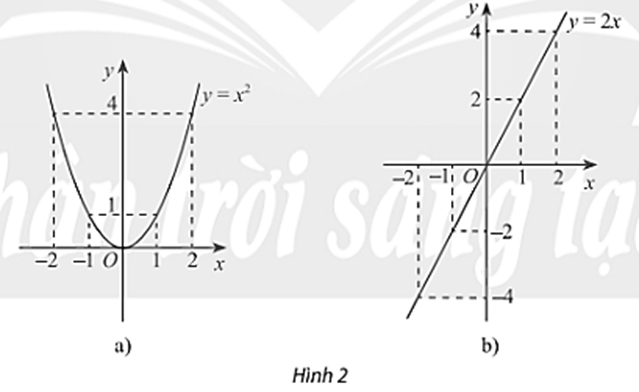
Khám phá 2: Xét hai hàm số y = x2, y = 2x và đồ thị của chúng trong Hình 2. Đối với mỗi trường hợp nêu mối liên hệ của giá trị hàm số tại 1 và – 1, 2 và – 2. Nhận xét về tính đối xứng của mỗi đồ thị hàm số.

Trả lời:

* Hàm số  y= x 2

- Ta thấy y(1) = y(-1) và y(2) = y(2)

- Đồ thị hàm số đối xứng qua trục Oy

* Hàm số y=2x

- Ta thấy y(1) = -y(-1) và y(2) = -y(-2)

- Đồ thị hàm số đối xứng qua điểm O

Thực hành 1: Chứng minh rằng hàm số y = sinx và hàm số y = cotx là các hàm số lẻ.

Trả lời:

+) Xét hàm số y = sinx có tập xác định D = ℝ

Lấy x ∈ D thì – x ∈ D và sin(– x) = – sinx. Do đó hàm số y = sinx là hàm số lẻ.

+) Xét hàm số y = cotx có tập xác định D = ℝ

Lấy x ∈ D thì – x ∈ D và cot(– x) = – cotx. Do đó hàm số y = cotx là hàm số lẻ.

Khám phá 3: Hãy chỉ ra một số thực T sao cho sin(x + T) = sinx với mọi x∈R

Trả lời:

T=2π

Thực hành 2: Xét tính tuần hoàn của hàm số y = cosx và hàm số y = cotx.

Trả lời:

Ta có: cos(x + 2π) = cosx với mọi x ∈ ℝ;

cot(x + π) = cotx với mọi $x\ne k\pi ,k\in Z$.

Do đó hàm số y = cosx và y = cotx là các hàm số tuần hoàn và tuần hoàn với chu kì T lần lượt là: 2π và π.

3. Đồ thị của các hàm số lượng giác

Khám phá 4: Hoàn thành bảng giá trị sau đây:

Trả lời:

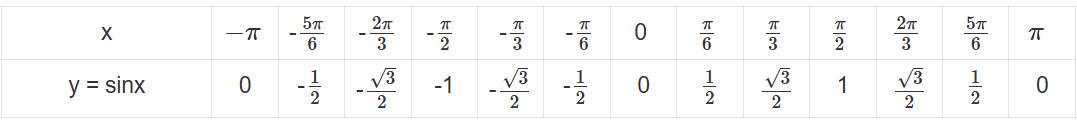
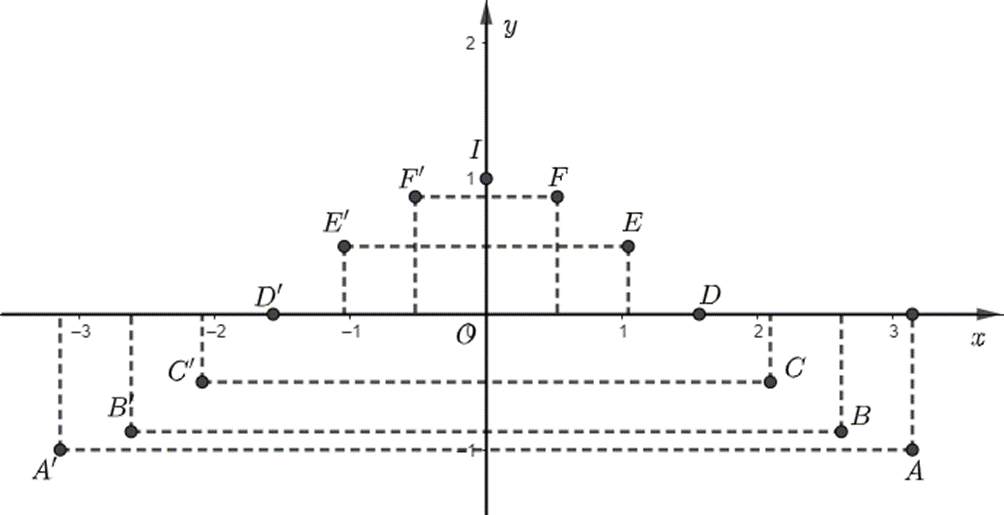
Khám phá 5: Hoàn thành bảng giá trị sau đây và xác định các điểm tương ứng trên mặt phẳng tọa độ.

Trả lời:

Với x = $-\pi$ thì y = cos($-\pi$) = -1. Ta có điểm A’(–π; – 1).

Với x = $-\frac{5\pi }{6}$ thì y = cos$\left(-\frac{5\pi }{6}\right)=\frac{\sqrt{3}}{2}$. Ta có điểm B'$\left(-\frac{5\pi }{6};-\frac{\sqrt{3}}{2}\right)$.

Với x = $-\frac{2\pi }{3}$ thì $y=\text{cos}\left(-\frac{2\pi }{3}\right)=-\frac{1}{2}$. Ta có điểm C'$\left(-\frac{2\pi }{3};-\frac{1}{2}\right)$.

Với x = $-\frac{\pi }{2}$ thì y = cos$\left(-\frac{\pi }{2}\right)=0$. Ta có điểm D'$\left(-\frac{\pi }{2};0\right)$.

Với x = $-\frac{\pi }{3}$ thì y = cos$\left(-\frac{\pi }{3}\right)=\frac{1}{2}$. Ta có điểm E'$\left(-\frac{\pi }{3};\frac{1}{2}\right)$.

Với x = $-\frac{\pi }{6}$ thì y = cos$\left(-\frac{\pi }{6}\right)=\frac{\sqrt{3}}{2}$. Ta có điểm F'$\left(-\frac{\pi }{6};\frac{\sqrt{3}}{2}\right)$.

Với x = 0 thì y = cos0 = 1. Ta có điểm I(0; 1).

Với x = $\frac{\pi }{6}$ thì y = cos$\left(\frac{\pi }{6}\right)=\frac{\sqrt{3}}{2}$. Ta có điểm F$\left(\frac{\pi }{6};\frac{\sqrt{3}}{2}\right)$.

Với x = $\frac{\pi }{3}$ thì y = cos$\left(\frac{\pi }{6}\right)=\frac{\sqrt{3}}{2}$. Ta có điểm F$\left(\frac{\pi }{6};\frac{\sqrt{3}}{2}\right)$.

Với x = $\frac{\pi }{2}$ thì y = cos$\left(\frac{\pi }{3}\right)=\frac{1}{2}$. Ta có điểm E$\left(\frac{\pi }{3};\frac{1}{2}\right)$.

Với x = $\frac{2\pi }{3}$ thì y = cos$\left(\frac{\pi }{2}\right)=0$. Ta có điểm D$\left(\frac{\pi }{2};0\right)$.

Với x = $\frac{5\pi }{6}$ thì y = cos$\left(\frac{5\pi }{6}\right)=-\frac{\sqrt{3}}{2}$. Ta có điểm $B\left(\frac{5\pi }{6};-\frac{\sqrt{3}}{2}\right)$.

Với x = $\pi$ thì $y=\text{cos}\left(\pi \right)=\text{cos}\pi =-1$. Ta có điểm A(π; – 1).

Khi đó ta có bảng:

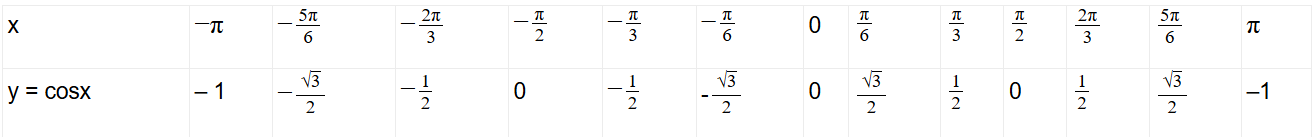
Biểu diễn các điểm trên trên mặt phẳng tọa độ ta được:

Thực hành 3: Cho hàm số y = cos x với x∈[−π2;π]

a) Vẽ đồ thị hàm số đã cho

b) Tại các điểm nào thì giá trị hàm số lớn nhất?

c)  Tìm các giá trị của x thuộc [−π4;5π4] sao cho sin(x−π4)<0

Trả lời:

a)

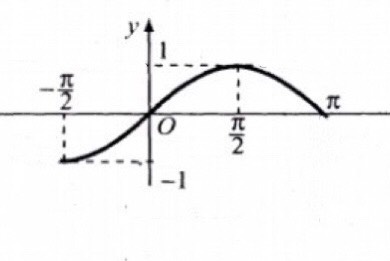
b) Tại điểm x=π2 giá trị hàm số là lớn nhất

c) Do x∈[−π4;5π4]

Nên (x−π4)∈[−π2;π]

Để sin(x−π4)<0 thì (x−π4)∈[−π2;0]

Suy ra x∈[−π4;π4]

Vận dụng 1: Li độ s (cm) của một con lắc đồng hộ theo thời gian t (giây) được cho bởi hàm số s=2cosπt. Dựa vào đồ thị của hàm số côsin, hãy xác định ở các thời điểm t nào trong 3 giây đầu thì con lắc có li độ lớn nhất

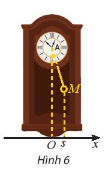
Trả lời:

Trong 3 giây đầu, 0≤t≤3 nên 0≤πt≤3π

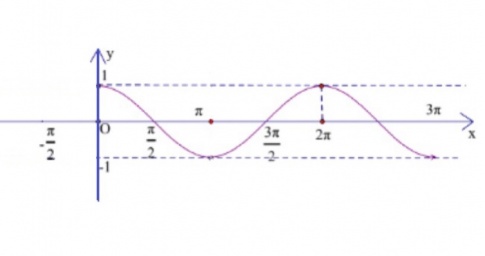
Dựa vào đồ thị hàm số côsin, ta thấy cosπt=1 khi πt=0 và πt=2π

Vậy con lắc có li độ lớn nhất tại các thời điểm t = 0 và t = 2 

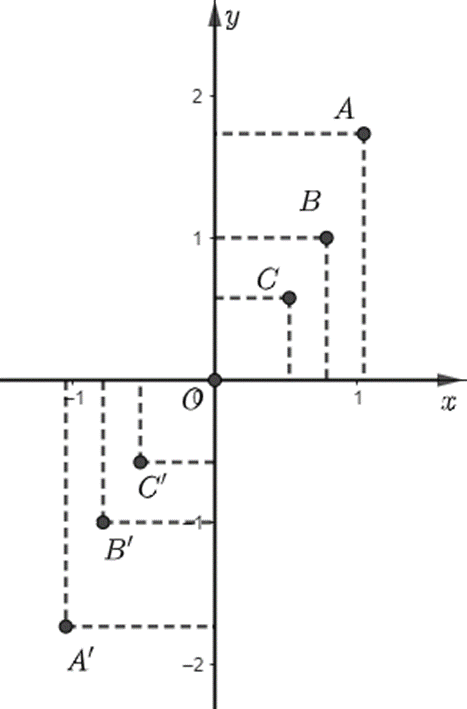
Khám phá 6: Hoàn thành bảng giá trị sau đây và xác định các điểm tương ứng trên mặt phẳng tọa độ.

Trả lời:

Với $x=-\frac{\pi }{3}$ thì $y=\tan \left(-\frac{\pi }{3}\right)=-\sqrt{3}$. Ta có điểm A'$\left(-\frac{\pi }{3};-\sqrt{3}\right)$.

Với $x=-\frac{\pi }{4}$ thì $y=\tan \left(-\frac{\pi }{4}\right)=-1$. Ta có điểm B'$\left(-\frac{\pi }{4};-1\right)$.

Với $x=-\frac{\pi }{6}$ thì $y=\tan \left(-\frac{\pi }{3}\right)=-\frac{\sqrt{3}}{3}$. Ta có điểm C'$\left(-\frac{\pi }{6};-\frac{\sqrt{3}}{3}\right)$.

Với $x=0$ thì $y=\tan \left(0\right)=0$. Ta có điểm O(0;0).

Với $x=\frac{\pi }{6}$ thì $y=\tan \left(\frac{\pi }{6}\right)=\frac{\sqrt{3}}{3}$. Ta có điểm C$\left(\frac{\pi }{6};\frac{\sqrt{3}}{3}\right)$.

Với $x=\frac{\pi }{4}$ thì $y=\tan \left(\frac{\pi }{4}\right)=1$. Ta có điểm B$\left(\frac{\pi }{4};1\right)$.

Với $x=\frac{\pi }{3}$ thì $y=\tan \left(\frac{\pi }{3}\right)=\sqrt{3}$. Ta có điểm A$\left(\frac{\pi }{3};\sqrt{3}\right)$.

Khi đó ta có bảng:

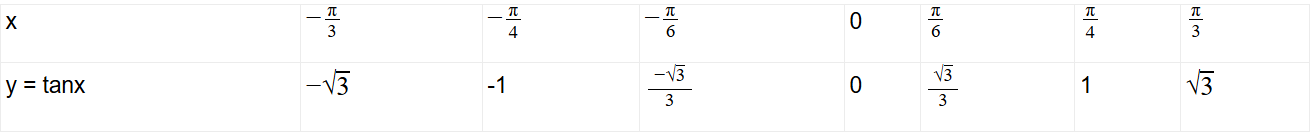
Biểu diễn các điểm trên trên mặt phẳng tọa độ ta được:

Khám phá 7: Hoàn thành bảng giá trị sau đây:

Trả lời:

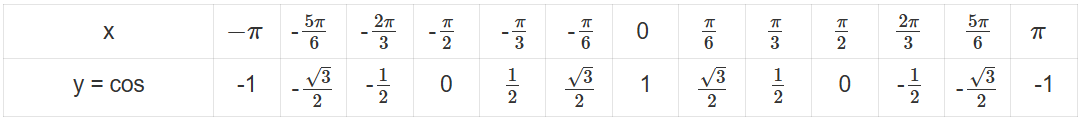
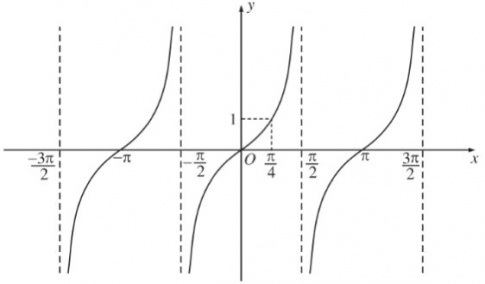
Thực hành 4: Cho hàm số y = cots với x ϵ(−π2;2π) và x∈Z.

a) Vẽ đồ thị hàm số đã cho

b) Có bao nhiêu giá trị x mà tại đó giá trị hàm số đã cho bằng 2?

Trả lời:

a)

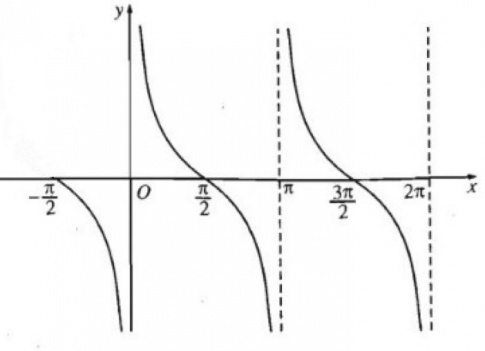
b) Từ độ thị, ta thấy có 2 giá trị x mà tại đó y = 2

Vận dụng 2: Trong Địa lí, phép chiếu hình trụ được sử dụng để vẽ một bản đồ phẳng như trong Hình 10. Trên bản đồ phẳng lấy đường xích đạo làm trục hoành và kinh tuyến 0o làm trục tung. Khi đó tung độ của một điểm có vĩ độ φo(−90<φ<90) được cho bởi hàm số y=20tan(π180φ) (cm). Sử dụng đồ thị hàm số tang, hãy cho biết những điểm ở vĩ độ nào nằm cách xích đạo 20cm trên bản đồ.

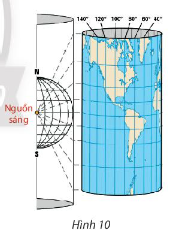
Trả lời:

Do φo(−90<φ<90) nên −π2<π180φ<π2

Bài tập

Bài tập 1: Các hàm số dưới đây có là hàm số chẵn hay hàm số lẻ không?

a) y = 5sin2x + 1;

b) y = cosx + sinx;

c) y = tan2x.

Trả lời:

a) Xét hàm số: y = 5sin2x + 1, có:

Tập xác định D = ℝ.

Nếu x ∈ D thì – x ∈ D có y( – x) = 5sin2(– x) + 1 = 5sin2 x + 1 = y(x).

Vì vậy hàm số này là hàm chẵn.

b) Xét hàm số: y = cosx + sinx

Tập xác định: D = ℝ

Nếu x ∈ D thì – x ∈ D có y( – x) = cos(– x) + sin(– x) = cosx – sin x ≠ y(x).

Vì vậy hàm số này không là hàm chẵn cũng không là hàm lẻ.

c) y = tan2x.

Tập xác định D = $R\backslash \left(\frac{\pi }{4}+k\pi ,k\in Z\right)$.

Nếu x ∈ D thì – x ∈ D có y( – x) = tan(– 2x) = – tan2x ≠ y(x).

Vì vậy hàm số này là hàm lẻ.

Bài tập 2: Tìm tập xác định của các hàm số sau:

a) y=1cosx

b) y=tan(x+π4)

c) y=12−sin2x

Trả lời:

a) Hàm số y xác định khi cosx≠0

Suy ra x≠π2+kπ

Vậy tập xác định của hàm số là R\{π2+kπ}

b) Hàm số y xác định khi cos(x+π4)≠0

Suy ra x+π4≠π2+kπ và x≠π4+kπ

Vậy tập xác định của hàm số là R\{π4+kπ}

c) Hàm số y xác định khi 2−sin2x≠0

Mà với mọi x∈R ta có: 0≤sin2α≤1 nên 1≤2−sin2α≤2

Vậy hàm số y xác định với mọi x∈R

Bài tập 3: Tìm tập giá trị của hàm số y = 2cosx + 1.

Trả lời:

Ta có: – 1 ≤ cosx ≤ 1 khi đó – 1 ≤ 2cosx + 1 ≤ 3.

Vậy tập giá trị của hàm số là D = [– 1; 3].

Bài tập 4: Dựa vào đồ thị của hàm số y = sinx, xác định các giá trị x∈[−π;π] thoả mãn sinx=12

Trả lời:

- Dựa vào đồ thị hình sin, ta thấy sinx=12 khi x=π6 và x=−π6

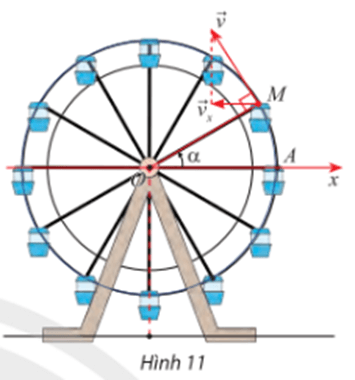
Bài tập 5: Khi đu quay hoạt động, vận tốc theo phương ngang của một cabin M phụ thuộc vào góc lượng giác α = (Ox, OM) theo hàm số vx = 0,3sin α (m/s) (Hình 11).

a) Tìm giá trị lớn nhất và giá trị nhỏ nhất của vx.

b) Dựa vào độ thị của hàm số sin, hãy cho viết trong các vòng quay đầu tiên (0 ≤ α ≤ 2π), góc α ở trong các khoảng nào thì vx tăng.

Trả lời:

a) Vì – 1 ≤ sin α ≤ 1 nên – 0,3 ≤ 0,3sin α ≤ 0,3.

Do đó giá trị nhỏ nhất của vx là – 0,3, giá trị lớn nhất của vx là 0,3.

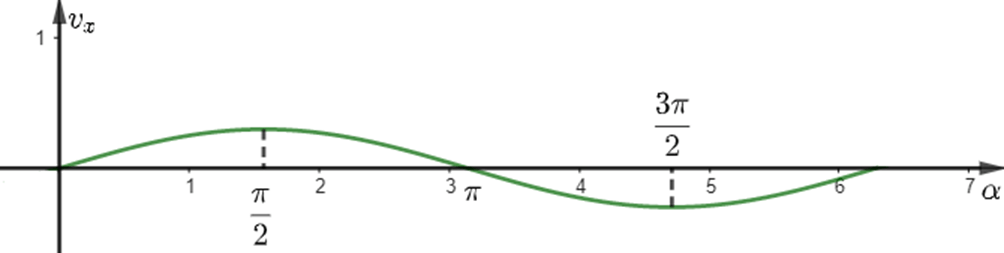
b) Ta có đồ thị hàm số:

Với góc $\alpha \in \left(0;\frac{\pi }{2}\right)$ hoặc $\alpha \in \left(\frac{3\pi }{2};2\pi \right)$ thì vx tăng.

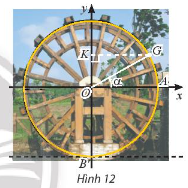
Bài tập 6: Khoảng cách từ tâm một guồng nước đến mặt nước và bán kính của guồng đều bằng 3m. Xét gàu G của guồng. Ban đầu gàu G nằm ở vị trí A (Hình 12)

a) Viết hàm số h biểu diễn chiều cao (tính bằng mét) của gàu G so với mặt nước theo góc α=(OA,OG)

b) Guồng nước quay hết mỗi vòng trong 30 giây. Dựa vào đồ thị của hàm số sin, hãy cho biết ở các thời điểm t nào trong 1 phút đầu, khoảng cách của gàu đến mặt nước bằng 1,5m.

Trả lời:

a) h=3+3.sinα

b) Trong 1 phút đầu, guồng nước quay được 2 vòng. Ta có 0≤α≤4π

Khi h = 1,5. Suy ra sinα=−12.

Khi đó, α=7π6; α=11π6; α=19π6 hoặc α=23π6

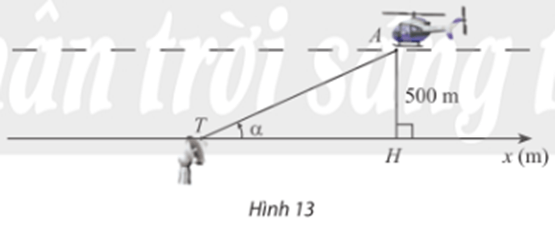
Bài tập 7: Trong Hình 13, một chiếc máy bay A bay ở độ cao 500m theo một đường thẳng đi ngang qua phía trên trạm quan sát T ở mặt đất. Hình chiếu vuông góc của A lên mặt đất là H, α là góc lượng giác (Tx, TA) (0 < α < π).

a) Biểu diễn tọa độ xH của điểm H trên trục Tx theo α.

b) Dựa vào đồ thị hàm số côtang, hãy cho biết với $\frac{\pi }{6}<\alpha <\frac{2\pi }{3}$ thì xH nằm trong khoảng nào. Làm tròn kết quả đến hàng phần mười.

Trả lời:

a) Xét tam giác AHT vuông tại H có:

$\cot \alpha =\frac{TH}{AH}\iff TH=AH.\cot \alpha =500.\cot \alpha$.

Vậy trên trục Tx tọa độ $x_H=500.\cot \alpha$.

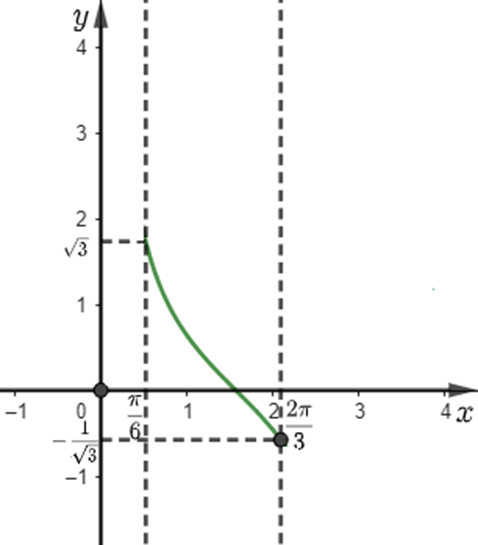
b) Ta có đồ thị của hàm số y = cotα trong khoảng $\frac{\pi }{6}<\alpha <\frac{2\pi }{3}$ là:

Khi đó $-\frac{1}{\sqrt{3}}<\cot \alpha <\sqrt{3}$

$\Rightarrow -\frac{500}{\sqrt{3}}<500\cot \alpha <500\sqrt{3}$ hay $-\frac{500}{\sqrt{3}}<x_H<500\sqrt{3}\iff -288,7<x_H<866$.