Giải SGK Toán 7 Cánh diều Bài 6: Dãy tỉ số bằng nhau

Khởi động: Có hai tỉ lệ thức:$\frac{1}{2}=\frac{2}{4}$ và $\frac{2}{4}=\frac{3}{6}$.

Làm thế nào để biểu diễn sự bằng nhau của ba tỉ số $\frac{1}{2};\frac{2}{4};\frac{3}{6}$?

Lời giải:

- Ta thấy $\frac{1}{2}=\frac{2}{4};\frac{2}{4}=\frac{3}{6}$ nên ta có thể viết là: $\frac{1}{2}=\frac{2}{4}=\frac{3}{6}$

I. Khái niệm

Hoạt động 1: So sánh từng cặp tỉ số trong ba tỉ số sau: $\frac{4}{6};\frac{8}{12};\frac{-10}{-15}$

Lời giải:

Vì 4.12  = 6.8 nên 46=812

Vì 8.(-15) = 12. (-10) nên 812=−10−15

Vì 4.(-15) = 6.(-10) nên 46=−10−15

Luyện tập, vận dụng 1: Viết dãy tỉ số bằng nhau từ các tỉ số: $\frac{1}{4};\frac{8}{32};\frac{13}{54};\frac{-9}{-36}$.

Lời giải:

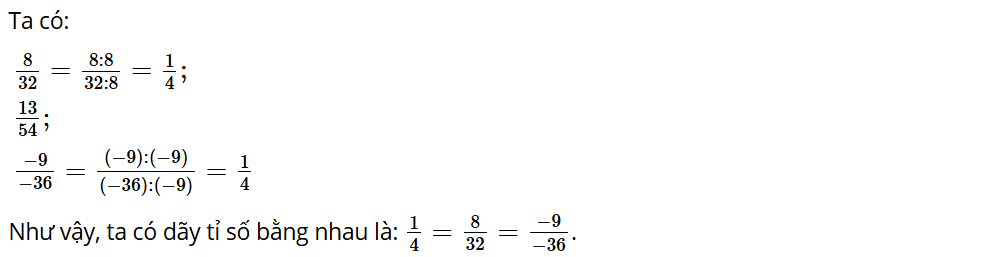
II. Tính chất

Hoạt động 2:

a) Cho tỉ lệ thức $\frac{6}{10}=\frac{9}{15}$

So sánh hai tỉ số $\frac{6+9}{10+15}$ và $\frac{6-9}{10-15}$ với các tỉ số trong tỉ lệ thức đã cho.

b) Cho tỉ lệ thức $\frac{a}{b}=\frac{c}{d}$ với b + d ≠ 0 và b – d ≠ 0.

Gọi giá trị chung của các tỉ số đã cho là k, tức là: k = $\frac{a}{b}=\frac{c}{d}$.

- Tính a theo b và k, tính c theo d và k.

- Tính tỉ số $\frac{a+c}{b+d}$ và $\frac{a-c}{b-d}$ theo k.

- So sánh mỗi tỉ số $\frac{a+c}{b+d}$ và $\frac{a-c}{b-d}$ với các tỉ số $\frac{a}{b}$ và $\frac{c}{d}$.

Lời giải:

a) Ta có: $\frac{6}{10}=\frac{6:2}{10:2}=\frac{3}{5}$

$\frac{9}{15}=\frac{9:3}{15:3}=\frac{3}{5}$

$\frac{6+9}{10+15}=\frac{15}{25}=\frac{15:5}{25:5}=\frac{3}{5}$

$\frac{6-9}{10-15}=\frac{-3}{-5}=\frac{3}{5}$

Hai tỉ số  $\frac{6+9}{10+15}$ và $\frac{6-9}{10-15}$ bằng với các tỉ số trong tỉ lệ thức $\frac{6}{10}=\frac{9}{15}$ vì cùng bằng $\frac{3}{5}$

Vậy $\frac{6}{10}=\frac{9}{15}=\frac{6+9}{10+15}=\frac{6-9}{10-15}$

b)

- Ta có: $k=\frac{a}{b}$ nên a = b.k;

$k=\frac{c}{d}$ nên c = d.k.

- Ta có: $\frac{a+c}{b+d}=\frac{b.k+d.k}{b+d}=\frac{k\left(b+d\right)}{b+d}=k$ (do b + d ≠ 0)

$\frac{a-c}{b-d}=\frac{b.k-d.k}{b-d}=\frac{k\left(b-d\right)}{b-d}=k$ (do b – d ≠ 0)

Vậy $\frac{a+c}{b+d}=k$; $\frac{a-c}{b-d}=k$

- Ta thấy: $\frac{a+c}{b+d}=k$ và $k=\frac{a}{b}=\frac{c}{d}$ nên $\frac{a+c}{b+d}=\frac{a}{b}=\frac{c}{d}$

$\frac{a-c}{b-d}=k$ và $k=\frac{a}{b}=\frac{c}{d}$ nên $\frac{a-c}{b-d}=\frac{a}{b}=\frac{c}{d}$

Luyện tập, vận dụng 2: Tìm hai số x, y biết: x : 1,2 = y : 0,4 và x – y = 2.

Lời giải:

Vì x:1,2=y:0,4 => x1,2=y0,4

Theo tính chất của dãy tỉ số bằng nhau, ta có:

x1,2=y0,4

=x−y1,2−0,4=20,8=2,5

=> Như vậy: x=1,2.2,5=3; y=0,4.2,5=1

Luyện tập, vận dụng 3: Tìm ba số x; y; z biết: x; y; z tỉ lệ với ba số 2; 3; 4 và x – y – z = 2.

Lời giải:

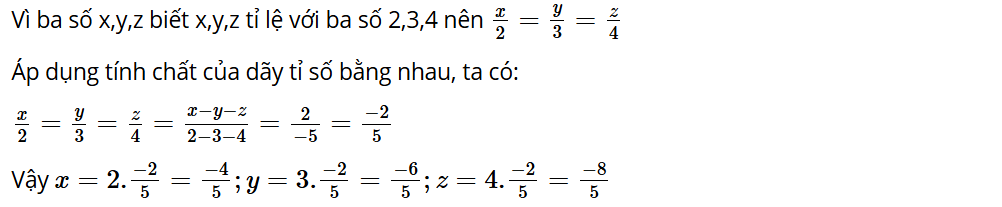
III. Ứng dụng

Luyện tập, vận dụng 4: Ba máy bơm cùng bơm nước vào một bể bơi không có nước, có dạng hình hộp chữ nhật, với các kích thước bể là 12 m; 10 m; 1,2 m. Lượng nước mà ba máy bơm được tỉ lệ với ba số 7; 8; 9. Mỗi máy cần bơm bao nhiêu mét khối nước để đầy bể bơi.

Lời giải:

Thể tích bể bơi hình hộp chữ nhật là: 12.10.1,2 = 144m3.

Gọi số mét khối nước ba máy bơm bơm được là x; y; z (m3) (x, y, z > 0)

Vì phải bơm vào bể bơi có thể tích là 144m3 nên ta có: x + y + z = 144 (m3)

Vì lượng nước mà ba máy bơm bơm được tỉ lệ với ba số 7; 8; 9 nên ta có dãy tỉ số bằng nhau: 

$\frac{x}{7}=\frac{y}{8}=\frac{z}{9}$

Áp dụng tính chất dãy tỉ số bằng nhau ta có: 

$\frac{x}{7}=\frac{y}{8}=\frac{z}{9}=\frac{x+y+z}{7+8+9}=\frac{144}{24}=6$

Khi đó: 

+) $\frac{x}{7}=6$ suy ra x = 6.7 = 42 (m3)

+) $\frac{y}{8}=6$ suy ra y = 6.8 = 48 (m3)

+) $\frac{z}{9}=6$ suy ra z = 6.9 = 54 (m3)

Vậy máy bơm thứ nhất cần bơm 42m3 nước, máy bơm thứ hai cần bơm 48m3 nước, máy bơm thứ ba cần bơm 54m3 nước.

Bài tập

Bài tập 1: Cho tỉ lệ thức $\frac{x}{7}=\frac{y}{2}$. Tìm hai số x; y biết: 

a) x + y = 18

b) x – y = 20.

Lời giải:

a. x+y=18         

Áp dụng tính chất của dãy tỉ số bằng nhau, ta có: x7=y2=x+y7+2=189=2

=> x=7.2=14

      y=2.2=4

b. x−y=20

Áp dụng tính chất của dãy tỉ số bằng nhau, ta có: x7=y2=x+y7−2=205=4

=> x=7.4=28

      y=2.4=8

Bài tập 2: Cho dãy tỉ số bằng nhau $\frac{x}{3}=\frac{y}{4}=\frac{z}{5}$. Tìm ba số x; y; z biết: 

a) x + y + z = 180;

b) x + y – z = 8

Lời giải:

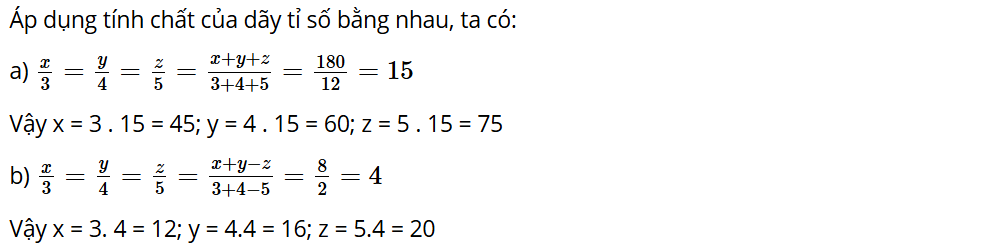
Bài tập 3: Cho ba số x; y; z sao cho: $\frac{x}{3}=\frac{y}{4};\frac{y}{5}=\frac{z}{6}$

a) Chứng minh: $\frac{x}{15}=\frac{y}{20}=\frac{z}{24}$.

b) Tìm ba số x; y; z biết x – y + z = –76.

Lời giải:

a) Ta có: 

+) $\frac{x}{3}=\frac{y}{4}$. Chia cả hai vế của đẳng thức cho 5 ta được: 

$\frac{x}{3}:5=\frac{y}{4}:5$ hay $\frac{x}{3}.\frac{1}{5}=\frac{y}{4}.\frac{1}{5}$. Do đó: $\frac{x}{15}=\frac{y}{20}$ (1)

+) $\frac{y}{5}=\frac{z}{6}$. Chia cả hai vế của đẳng thức cho 4 ta được: 

$\frac{y}{5}:4=\frac{z}{6}:4$ hay $\frac{y}{5}.\frac{1}{4}=\frac{z}{6}.\frac{1}{4}$. Do đó: $\frac{y}{20}=\frac{z}{24}$ (2)

Từ (1) và (2) suy ra: $\frac{x}{15}=\frac{y}{20}=\frac{z}{24}$

b) Từ tỉ lệ thức $\frac{x}{15}=\frac{y}{20}=\frac{z}{24}$ áp dụng tính chất dãy tỉ số bằng nhau ta có: 

$\frac{x}{15}=\frac{y}{20}=\frac{z}{24}=\frac{x-y+z}{15-20+24}=\frac{-76}{19}=-4$

Khi đó:

+) $\frac{x}{15}=-4$ suy ra x = (–4).15 = –60

+) $\frac{y}{20}$ = –4 suy ra y = (–4).20 = –80

+) $\frac{z}{24}$ = –4 suy ra z = (–4).24 = –96.

Vậy x = –60; y = –80; z = –96.

Bài tập 4: Tỉ lệ phần trăm của lượng khí oxygen thải ra môi trường và lượng khí carbon dioxide hấp thụ trong quá trình quang hợp của lá cây Atriplex rosea (một loài thực vật thân mềm có hoa giống hoa cúc) ở nhiệt độ 27°C và trong điều kiện bình thường là 21%.

(Nguồn: A.Kaplan and O.Bjokman, Ratio of CO2 Uptake to O2 Evolution during Photosynthesis in Higher Plants, Z.Pflanzanphysiol. Bd. 96. S(1980), p. 185 – 188)

Tính lượng khí oxygen thải ra môi trường và lượng khí carbon dioxide hấp thụ trong quá trình quang hợp của lá cây Atriplex rosea ở nhiệt độ 27°C và trong điều kiện bình thường, biết lượng khí carbon dioxide lá cây hấp thụ nhiều hơn lượng khí oxygen thải ra môi trường là 15,8 g.

Lời giải:

Bài tập 5: Một mảnh vườn có dạng hình chữ nhật với tỉ số giữa độ dài hai cạnh của nó bằng $\frac{3}{5}$ và chu vi bằng 48 m.

a) Tính chiều dài, chiều rộng của mảnh vườn đó.

b) Tính diện tích của mảnh vườn đó.

Lời giải:

Gọi độ dài 2 cạnh hình chữ nhật là x,y(m)(x,y>0)

Vì tỉ số giữa độ dài hai cạnh của nó bằng 35 nên xy=35=>x3=y5

Vì chu vi của mảnh đất hình chữ nhật là 48 m nên 2.(x+y)=48 nên x+y=48:2=24

Áp dụng tính chất của dãy tỉ số bằng nhau, ta có:

x3=y5=x+y3+5=248=3 =>x=3.3=9; y=5.3=15

Vậy mảnh vườn hình chữ nhật có diện tích là: S = 9.15 = 135 (m2)

Bài tập 6: Trong một đợt quyên góp sách ủng hộ các bạn vùng lũ lụt, số sách mà ba lớp 7A; 7B; 7C quyên góp được tỉ lệ với ba số 5; 6; 8. Tính số sách cả ba lớp đã quyên góp, biết số sách lớp 7C quyên góp được nhiều hơn số sách của lớp 7A quyên góp là 24 quyển.

Lời giải:

Bài tập 7: Trên quần đảo Trường Sa của Việt Nam, cây bàng vuông, cây phong ba, cây mù u là những loài cây có sức sống mãnh liệt, chịu đựng được tàn phá của thiên nhiên, biển mặn và có thời gian sinh trường lâu. Nhân ngày Tết trồng cây, các chiến sĩ đã trồng tổng cộng 36 cây bàng vuông, cây phong ba và cây mù u trên các đảo. Số cây bàng vuông, cây phong ba và cây mù u đã trồng tỉ lệ với ba số 5; 4; 3. Hỏi các chiến sĩ đã trồng mỗi loại bao nhiêu cây?

Lời giải:

Gọi số cây bàng vuông, cây phong ba và cây mù u các chiến sĩ đã trồng lần lượt là x, y, z (x; y; z $\in N^{\ast }$ ).

Vì tổng số cây đã trồng là 36 nên ta có: x + y + z = 36.

Vì số cây bàng vuông, cây phong ba và cây mù u đã trồng tỉ lệ với ba số 5; 4; 3 nên ta có: $\frac{x}{5}=\frac{y}{4}=\frac{z}{3}$.

Áp dụng tính chất dãy tỉ số bằng nhau ta có: 

$\frac{x}{5}=\frac{y}{4}=\frac{z}{3}=\frac{x+y+z}{5+4+3}=\frac{36}{12}=3$

Khi đó:

+) $\frac{x}{5}=3$ suy ra x = 3.5 = 15 (thoả mãn);

+) $\frac{y}{4}=3$ suy ra y = 3.4 =12 (thoả mãn);

+) $\frac{z}{3}=3$ suy ra z = 3.3 = 9 (thoả mãn).

Vậy số cây bàng vuông đã trồng là 15 cây; số cây phong ba đã trồng là 12 cây; số cây mù u đã trồng là 9 cây.