Giải SGK Toán 7 Cánh diều Bài 7: Đại lượng tỉ lệ thuận - Giải SGK Toán 7 - Cánh Diều

Khởi động: Một chiếc máy bay bay với vận tốc không đổi là 900km/h. Quãng đường s (km) mà máy bay đó bay được và thời gian di chuyển t (h) là hai đại lượng liên hệ với nhau như nào?

Lời giải:

Ta có: s = v . t = 900. t.

Do đó, quãng đường s (km) mà máy bay đó bay được và thời gian di chuyển t (h) là hai đại lượng tỉ lệ thuận theo hệ số tỉ lệ 900.

I. Khái niệm

Hoạt động 1: Chiều dài x (m) và khối lượng m (kg) của thanh sắt phi 18 được liên hệ theo công thức m = 2x. Tìm số thích hợp cho $?$ trong bảng sau:

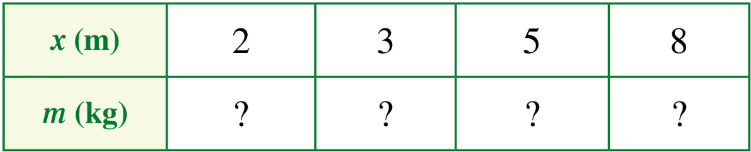
Lời giải:

Công thức liên hệ giữa chiều dài và khối lượng của thanh sắt phi 18 là: m = 2.x.

+) Với x = 2 thì m = 2.2 = 4

+) Với x = 3 thì m = 2.3 = 6

+) Với x = 5 thì m = 2.5 = 10

+) Với x = 8 thì m = 2.8 = 16

Ta có bảng sau:

Luyện tập, vận dụng 1: Một chiếc ô tô chuyển động đều với vận tốc 65km/h.

a) Viết công thức tính quãng đường đi được s (km) theo thời gian t (h) của chuyển động.

b) s và t có phải hai đại lượng tỉ lệ thuận hay không? Nếu có hãy xác định hệ số tỉ lệ của s đối với t.

c) Tính giá trị của s khi t = 0,5; t = $\frac{3}{2}$ ; t = 2.

Lời giải:

a. Công thức tính quãng đường đi được theo thời gian: S = v.t = 65.t

b. Vì s và t liên hệ với nhau theo công thức s = 65t => s và t là hai đại lượng tỉ lệ thuận.

Hệ số tỉ lệ của s đối với t là: 65

c. Giá trị của s khi t = 0,5; t = 32; t = 2 lần lượt là: 32,5; 43,33...; 130.

II. Tính chất

Hoạt động 2: Cho biết x; y là hai đại lượng tỉ lệ thuận với nhau:

a) Hãy xác định hệ số tỉ lệ của y đối với x.

b) So sánh các tỉ số: $\frac{y_{1}}{x_{1}}; \frac{y_{2}}{x_{2}}; \frac{y_{3}}{x_{3}}$ .

c) So sánh các tỉ số $\frac{x_{1}}{x_{2}}$ và $\frac{y_{1}}{y_{2}}$ ; $\frac{x_{1}}{x_{3}}$ và $\frac{y_{1}}{y_{3}}$ .

Lời giải:

III. Một số bài toán

Luyện tập, vận dụng 2: Một máy in trong 5 phút in được 120 trang. Hỏi trong 3 phút máy in đó in được bao nhiêu trang?

Lời giải:

Gọi x (phút), y (trang) lần lượt là số phút và số trang máy in in được (x; y > 0).

Khi đó, mối quan hệ giữa số phút và số trang in là hai đại lượng tỉ lệ thuận với nhau, áp dụng tính chất tỉ lệ thuận ta có: $\frac{x_{1}}{x_{2}} = \frac{y_{1}}{y_{2}}$ .

Thay x1 = 5, y1 = 120, x2 = 3 ta có: $\frac{5}{3} = \frac{120}{y_{2}}$ nên $y_{2} = \frac{120.3}{5} = 72$

Vậy trong 3 phút máy in đó in được 72 trang.

Luyện tập, vận dụng 3: Nhà trường phân công ba lớp 7A; 7B; 7C chăm số 54 cây xanh trong trường. Số cây mỗi lớp cần chăm sóc tỉ lệ thuận với số học sinh của lớp. Biết lớp 7A có 40 học sinh; lớp 7B có 32 học sinh; lớp 7C có 36 học sinh. Tính số cây mỗi lớp cần chăm sóc.

Lời giải:

Gọi số cây mỗi lớp cần chăm sóc là x,y,z (x,y,z > 0)

Vì số cây mỗi lớp cần chăm sóc tỉ lệ thuận với số học sinh của lớp nên ta có: x4=y32=z36

Theo tính chất của dãy tỉ số bằng nhau ta có:

x4=y32=z36=x+y+z40+32+36=54108=12

=> x=40.12=20; x=32.12=16; z=36.12=18

Vậy số cây mỗi lớp cần chăm sóc là:

Lớp 7A: 20 cây

Lớp 7B: 16 cây

Lớp 7C: 18 cây

Bài tập

Bài tập 1: Các giá trị tương ứng của khối lượng m (g) và thể tích V (cm3) được cho bởi bảng sau:

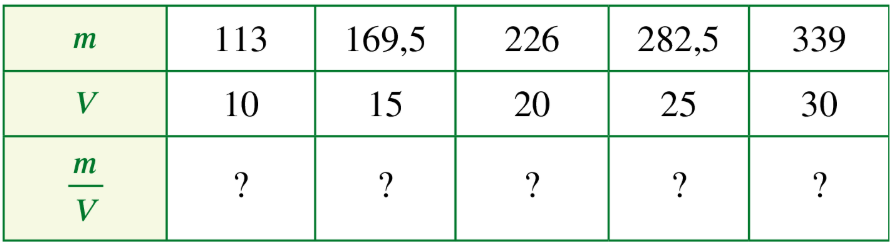
a) Tìm số thích hợp cho $?$ .

b) Hai đại lượng m và V có tỉ lệ thuận với nhau không? Vì sao?

Lời giải:

+) Với m = 113 và V = 10 nên $\frac{m}{V} = \frac{113}{10} = 11,3$

+) Với m = 169,5 và V = 15 nên $\frac{m}{V} = \frac{169,5}{15} = 11,3$

+) Với m = 226 và V = 20 nên $\frac{m}{V} = \frac{226}{20} = 11,3$

+) Với m = 282,5 và V = 25 nên $\frac{m}{V} = \frac{282,5}{25} = 11,3$

+) Với m = 339 và V = 30 nên $\frac{m}{V} = \frac{339}{30} = 11,3$

Ta có bảng sau:

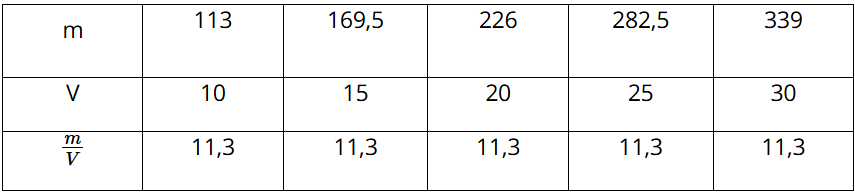
b) Hai đại lượng m và V tỉ lệ thuận với nhau vì từ kết quả câu a ta thấy tỉ số $\frac{m}{V}$ không đổi..

Bài tập 2: Cho biết x,y là hai đại lương tỉ lệ thuận với nhau:

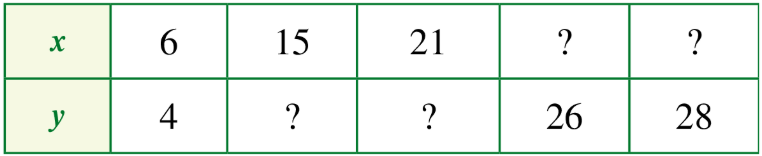
a) Xác định hệ số tỉ lệ của y đối với x. Viết công thức tính y theo x.

b) Xác định hệ số tỉ lệ của x đối với y. Viết công thức tính x theo y.

c) Tìm số thích hợp cho $?$ .

Lời giải:

c) Ta sử dụng các công thức y = $\frac{2}{3} x$ và x = $\frac{3}{2} y$ tính được:

Với x = 15 thì $y = \frac{2}{3} .15 = 6$ ;

Với x = 21 thì $y = \frac{2}{3} .21 = 14$ ;

Với y = 26 thì $x = \frac{3}{2} .26 = 39$ ;

Với y = 28 thì $x = \frac{3}{2} .28 = 42$ .

Ta có bảng sau:

Bài tập 3: Trung bình cứ 5 l nước biển chứa 175 g muối. Hỏi trung bình 12 l nước biển chứa bao nhiêu gam muối?

Lời giải:

Gọi khối lượng muối có trong 12l nước biển là x(g)(x>0)

Vì lượng nước biển và lượng muối nó chứa là hai đại lượng tỉ lệ thuận nên theo tính chất của hai đại lượng tỉ lệ thuận, ta có: 1755=x12=>x=175.125=420

=> Trung bình 12l nước biển chứa 420g muối.

Bài tập 4: Cứ 12 phút, một chiếc máy làm được 27 sản phẩm. Để làm được 45 sản phẩm như thế thì chiếc máy đó cần bao nhiêu phút

Lời giải:

Gọi x (phút), y (sản phầm) lần lượt là số phút và số sản phẩm mà chiếc máy đó làm được (x; y > 0).

Khi đó, mối quan hệ giữa số phút và số sản phẩm mà chiếc máy đó làm được là hai đại lượng tỉ lệ thuận với nhau, áp dụng tính chất tỉ lệ thuận ta có: .

Thay x1 = 12, y1 = 27, y2 = 45 ta có: $\frac{12}{27} = \frac{x_{2}}{45}$ nên $x_{2} = \frac{12.45}{27} = 20$

Vậy để làm được 45 sản phẩm chiếc máy đó cần 20 phút.

Bài tập 5: Để làm thuốc ho người ta ngâm chanh đào với mật ong và đường phèn theo tỉ lệ: Cứ 0,5 kg chanh đào thì cần 250 g đường phèn và 0,5 l mật ong. Với tỉ lệ đó, nếu muốn ngâm 2,5 kg chanh đào thì cần bao nhiêu ki – lô – gam đường phèn và bao nhiêu lít mật ong?

Lời giải:

Bài tập 6: Theo như công bố chính thức từ hãng sản xuất, chiếc xe ô tô của cô Hạnh có mức tiêu thụ nhiên liệu như sau:

+) 9,9 l/100 km trên đường hỗn hợp;

+) 13,9 l/100 km trên đường đô thị;

+) 7,5 l/100 km trên đường cao tốc.

a) Theo thông số trên, nếu trong bình xăng của chiếc xe ô tô đó có 65 lít xăng thì cô Hạnh đi được bao nhiêu ki – lô – mét (làm tròn kết quả đến hàng đơn vị) khi cô đi trên đường đô thị? Đường hỗn hợp? Đường cao tốc?

b) Để đi quãng đường 400 km trên đường đô thị, trong bình xăng chiếc xe ô tô của cô Hạnh cần có tối thiểu bao nhiêu lít xăng?

c) Để đi quãng đường 300 km trên đường hỗn hợp và 300km trên đường cao tốc, trong bình xăng chiếc xe ô tô của cô Hạnh cần tối thiểu bao nhiêu lít xăng?

Lời giải:

Đường đô thị cô Hạnh đi được: 65 : 13,9 . 100 ≈ 468 (km)

Đường hỗn hợp cô Hạnh đi được: 65 : 9,9 . 100 ≈ 657 (km)

Đường cao tốc cô Hạnh đi được: 65 : 7,5 . 100 ≈ 867 (km)

b) Để đi quãng đường 400 km trên đường đô thị, bình xăng ô tô của Hạnh cần có tối thiểu: 400 : 100 . 13,9 = 55,6 (lít)

c) Để đi quãng đường 300 km trên đường hỗn hợp và 300 km trên đường cao tốc, trong bình xăng chiếc xe ô tô của cô Hạnh cần có tối thiểu: 300: 100. 9,9 + 300 : 100 . 7,5 = 52,2 (lít).